C语言汉诺塔
hania_w 人气:01、汉诺塔是如何实现的
下面是有三个盘子的示例:
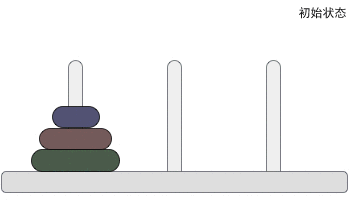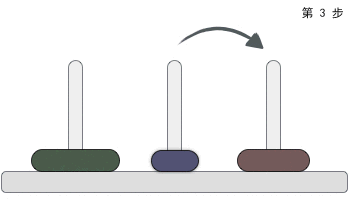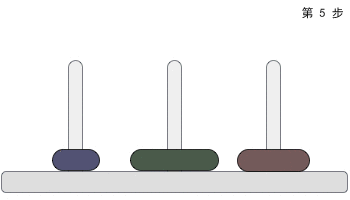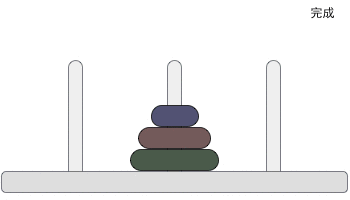
从左到右一次是 A柱 B柱 C柱
A柱:起始位置
B柱:目标位置
C柱:过度位置
汉诺塔为题即是,将A柱上的所有盘子移动到B柱上,且每次只能移动一个盘子,并且小盘子必须在大盘子上面
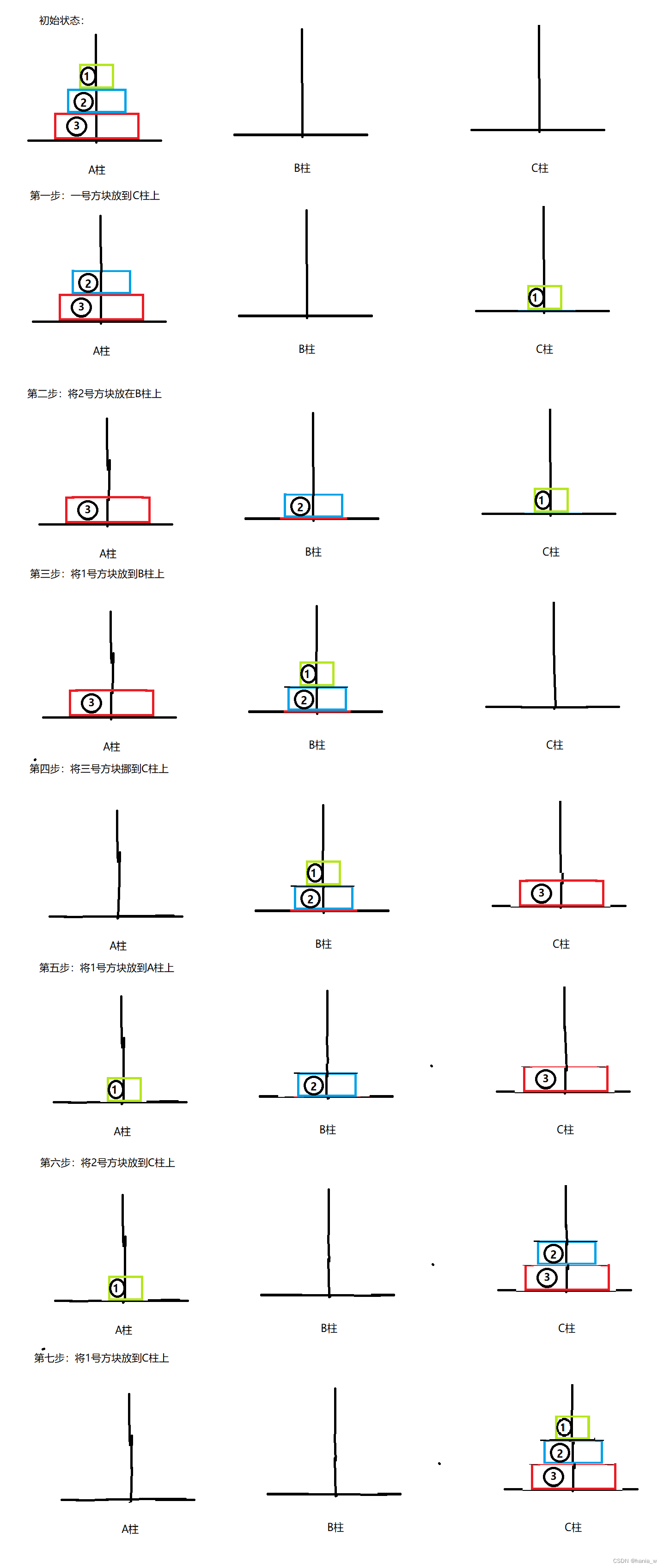
2、汉诺塔问题画图详解
下面的例子是以A柱为起始位置,B柱为中间位置,C柱为目标位置的
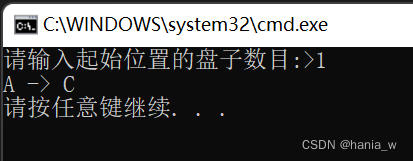
如果初始状态下:A柱只有一个盘子:A->C
A柱有两个盘子:A->B A->C B->C
A柱有三个盘子:A->C A->B C->B A->C B->A
B->C A->C
下面我们画图来详细解释一下初始状态下为三个盘子的方法:
3、汉诺塔问题代码解释
//用c语言解决汉诺塔问题(函数递归)
#include<stdio.h>
//n:代表盘子的个数
//a:起始位置
//b:过度位置
//c:目的位置
void Move(char x1, char x2)
{
printf("%c -> %c ",x1,x2);//打印盘子的移动情况
}
void Hanoi(int n, char x1, char x2, char x3)
{
if (n == 1)//递归的终止条件
{
Move(a, c);//当起始位置只有一个盘子时,直接将他挪到终止位置
}
else
{
Hanoi(n - 1, a, c, b);
//将除掉最底部的一个盘子外,其余盘子通过起始位
//置A柱,过度位置C柱,最终移动到B柱上
Move(a, c);//接着将A柱上的盘子直接移动到C柱上
Hanoi(n - 1, b, a, c);
//把B柱上的n-1个盘子,通过A柱,全部移动到C柱上
}
}
int main()
{
char a = 'A';
char b = 'B';
char c = 'C';
int n = 0;
printf("请输入起始位置的盘子数目:>");
scanf("%d", &n);
Hanoi(n, a, b, c);
printf("\n");
return 0;
}
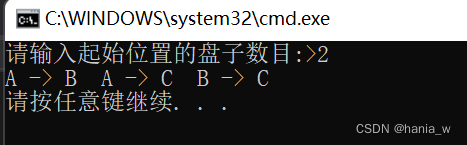


当A柱起始位置有三个盘子是与我们分析的结果是一样的
总结
汉诺塔问题,需要用到递归思想,即从大到小考虑,
搞清楚每一步的起始位置与目标位置,巧妙借助过度位置的柱子去解决问题!
加载全部内容