Java Floyd算法
chengqiuming 人气:0一 问题描述
求节点0到节点2的最短路径。
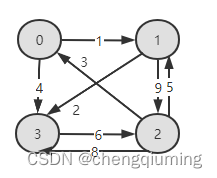
二 代码
package graph.floyd;
import java.util.Scanner;
public class Floyd {
static final int MaxVnum = 100; // 顶点数最大值
static final int INF = 0x3f3f3f3f; //无穷大
static final int dist[][] = new int[MaxVnum][MaxVnum]; // 最短距离
static final int p[][] = new int[MaxVnum][MaxVnum]; // 前驱数组
static final boolean flag[] = new boolean[MaxVnum]; // 如果 s[i] 等于 true,说明顶点 i 已经加入到集合 S ;否则顶点 i 属于集合 V-S
static int locatevex(AMGraph G, char x) {
for (int i = 0; i < G.vexnum; i++) // 查找顶点信息的下标
if (x == G.Vex[i])
return i;
return -1; // 没找到
}
static void CreateAMGraph(AMGraph G) {
Scanner scanner = new Scanner(System.in);
int i, j;
char u, v;
int w;
System.out.println("请输入顶点数:");
G.vexnum = scanner.nextInt();
System.out.println("请输入边数:");
G.edgenum = scanner.nextInt();
System.out.println("请输入顶点信息:");
// 输入顶点信息,存入顶点信息数组
for (int k = 0; k < G.vexnum; k++) {
G.Vex[k] = scanner.next().charAt(0);
}
//初始化邻接矩阵所有值为0,如果是网,则初始化邻接矩阵为无穷大
for (int m = 0; m < G.vexnum; m++)
for (int n = 0; n < G.vexnum; n++)
if (m != n)
G.Edge[m][n] = INF;
else
G.Edge[m][n] = 0; // 注意m==n时,设置为 0
System.out.println("请输入每条边依附的两个顶点及权值:");
while (G.edgenum-- > 0) {
u = scanner.next().charAt(0);
v = scanner.next().charAt(0);
w = scanner.nextInt();
i = locatevex(G, u);// 查找顶点 u 的存储下标
j = locatevex(G, v);// 查找顶点 v 的存储下标
if (i != -1 && j != -1)
G.Edge[i][j] = w; //有向图邻接矩阵
else {
System.out.println("输入顶点信息错!请重新输入!");
G.edgenum++; // 本次输入不算
}
}
}
static void Floyd(AMGraph G) { // 用 Floyd 算法求有向网 G 中各对顶点 i 和 j 之间的最短路径
int i, j, k;
for (i = 0; i < G.vexnum; i++) // 各对结点之间初始已知路径及距离
for (j = 0; j < G.vexnum; j++) {
dist[i][j] = G.Edge[i][j];
if (dist[i][j] < INF && i != j)
p[i][j] = i; // 如果 i 和 j 之间有弧,则将 j 的前驱置为 i
else p[i][j] = -1; // 如果 i 和 j 之间无弧,则将 j 的前驱置为 -1
}
for (k = 0; k < G.vexnum; k++)
for (i = 0; i < G.vexnum; i++)
for (j = 0; j < G.vexnum; j++)
if (dist[i][k] + dist[k][j] < dist[i][j]) { // 从 i 经 k 到 j 的一条路径更短
dist[i][j] = dist[i][k] + dist[k][j]; // 更新dist[i][j]
p[i][j] = p[k][j]; // 更改 j 的前驱
}
}
static void print(AMGraph G) { // 输出邻接矩阵
int i, j;
for (i = 0; i < G.vexnum; i++) {//输出最短距离数组
for (j = 0; j < G.vexnum; j++)
System.out.print(dist[i][j] + "\t");
System.out.println();
}
System.out.println();
for (i = 0; i < G.vexnum; i++) {//输出前驱数组
for (j = 0; j < G.vexnum; j++)
System.out.print(p[i][j] + "\t");
System.out.println();
}
}
static void DisplayPath(AMGraph G, int s, int t) { // 显示最短路径
if (p[s][t] != -1) {
DisplayPath(G, s, p[s][t]);
System.out.print(G.Vex[p[s][t]] + "-->");
}
}
public static void main(String[] args) {
char start, destination;
int u, v;
AMGraph G = new AMGraph();
CreateAMGraph(G);
Floyd(G);
print(G);
System.out.print("请依次输入路径的起点与终点的名称:");
Scanner scanner = new Scanner(System.in);
start = scanner.next().charAt(0);
destination = scanner.next().charAt(0);
u = locatevex(G, start);
v = locatevex(G, destination);
DisplayPath(G, u, v);
System.out.println(G.Vex[v]);
System.out.println("最短路径的长度为:" + dist[u][v]);
System.out.println();
}
}
class AMGraph {
char Vex[] = new char[Floyd.MaxVnum];
int Edge[][] = new int[Floyd.MaxVnum][Floyd.MaxVnum];
int vexnum; // 顶点数
int edgenum; // 边数
}三 实现
白色为输出,绿色为输入。
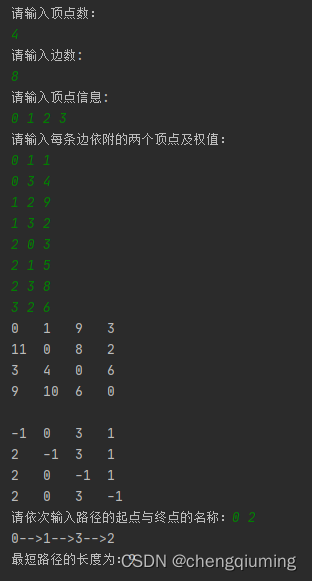
加载全部内容