Java二叉查找树增删查

时间:2022-09-08 WX7251 人气:0

定义

二叉查找树（ADT）是一个具有对于树种的某个节点X,它的左节点都比X小，它的右节点都比X大的二叉树。如下就是一个符合

要求的二叉查找树：

增加节点

1.定义节点类:

class Node{
    int val;
    Node left;
    Node right;
    public Node(int val){
        this.val=val;
    }
}

2.插入元素

我们采用递归的方法：

1.判断与根节点是否相同，相同无需操作

2.比根元素小往左边查找，左节点不存在的话则作为左节点插入即可

3.比根元素大往右边查找，右节点不存在的话则作为右节点插入即可

代码实现如下：

Node root;
 
    /**
     * 添加元素
     * @param val
     */
    public void add(int val){
        if(root==null){
            root=new Node(val);
            return;
        }
        addNode(val,root);
    }
    private void addNode(int val,Node root){
        if(root==null || root.val==val){
            return;
        }
        if(root.val>val){
            if(root.left==null){
                root.left=new Node(val);
            }else {
                addNode(val,root.left);
            }
        }else {
            if(root.right==null){
                root.right=new Node(val);
            }else {
                addNode(val,root.right);
            }
        }
    }

查询节点

我们采用递归的方法：

1.判断与根节点是否相同，相同则返回true

2.比根元素小往左边查找，左节点为null则返回false表示不存在

3.比根元素大往右边查找，右节点为null则返回false表示不存在

代码实现如下:

/**
     * 判断指定值是否存在
     * @param val 指定值
     * @return true--存在   false--不存在
     */
    public boolean findVale(int val){
        return isExit(root,val);
    }
 
    private boolean isExit(Node node,int val){
        if(node==null){
            return false;
        }
        if(node.val==val){
            return true;
        }else if(node.val>val){
            return isExit(node.left,val);
        }else {
            return isExit(node.right,val);
        }
    }

删除节点

删除元素时要判断元素的情况：

1.删除的元素没有叶子节点，直接删除，如删除值为1的节点，虽然平衡性不是太好，但是还是符合二叉查找树的特性

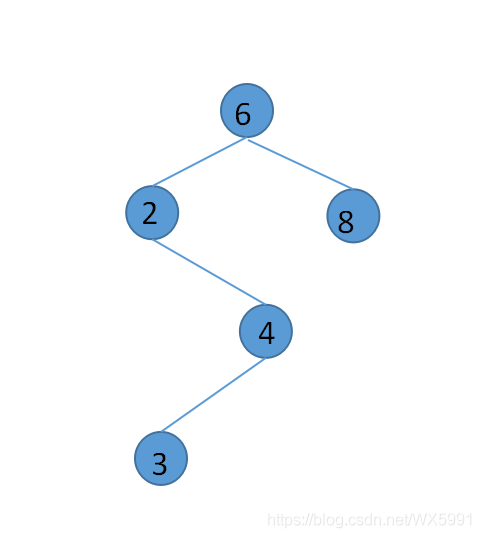
2.删除的元素只有一个节点，删除元素并将指针指向其子节点，如删除值为4的节点:

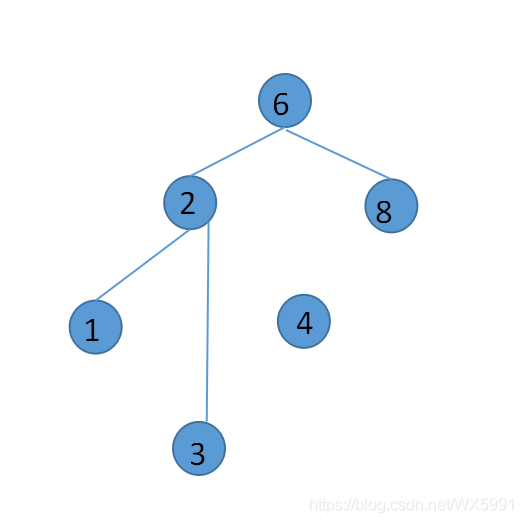
3.删除的元素有左右两个节点，从右节点中找出大于该节点的最小节点，作为新的节点A,如删除节点值为2的节点:

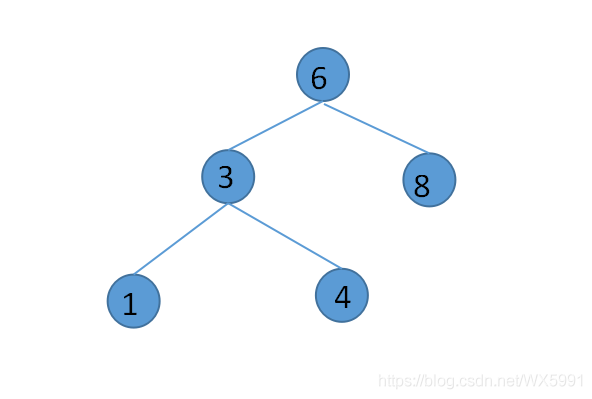
代码实现如下:

/**
     * 删除元素
     * 1.删除的元素没有叶子节点，直接删除
     * 2.删除的元素只有一个节点，删除元素并将指针指向其子节点
     * 3.删除的元素有两个节点，从右节点中找出大于该元素的最小值，作为新的节点
     * @param val
     */
    public void deleteElement(int val){
        deleteElement(null,root,val,true);
    }
 
    /**
     * 删除元素
     * @param prev 父节点
     * @param root 当前节点
     * @param val  删除值
     * @param isright  是否是右节点
     */
    private void deleteElement(Node prev,Node root,int val,boolean isright){
        if(root.val==val){
            //删除的元素没有叶子节点，直接删除
            if(root.left==null &&  root.right==null){
                changeValue(prev,null,isright);
            }else if(root.left!=null &&  root.right!=null){
                //3.删除的元素有两个节点，从右节点中找出大于该元素的最小值，作为新的节点
                changeValue(prev,new Node(findMinGt(root,root.right,true)),isright);
                if(prev==null){
                    //对于头结点的删除特殊处理
                    prev=this.root;
                    prev.left=root.left;
                    prev.right=root.right;
                    return;
                }
                if(isright){
                    prev.right.right=root.right;
                    prev.right.left=root.left;
                }else {
                    prev.left.right=root.right;
                    prev.left.left=root.left;
                }
            }//删除的元素只有一个节点，删除元素并将指针指向其子节点
            else if(root.left!=null){
                changeValue(prev,root.left,isright);
            }else {
                changeValue(prev,root.right,isright);
            }
            return;
        }
        if(root.val>val){
            deleteElement(root,root.left,val,false);
        }else{
            deleteElement(root,root.right,val,true);
        }
    }
    //改变元素值
    private void changeValue(Node prev,Node value,boolean isright){
        if(prev==null){
            root=value;
            return;
        }
        if(isright){
            prev.right=value;
        }else {
            prev.left=value;
        }
    }
    //寻找大于根节点的最小值
    private int findMinGt(Node prev,Node root,boolean isRight){
        if(root.left==null && root.right==null){
            changeValue(prev,null,isRight);
            return root.val;
        }
        if(root.left==null){
            changeValue(prev,null,isRight);
            return root.val;
        }
        return findMinGt(root,root.left,false);
    }

加载全部内容