Python散点密度图
气象水文科研猫 人气:0方式一
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import gaussian_kde
from mpl_toolkits.axes_grid1 import make_axes_locatable
from matplotlib import rcParams
config = {"font.family":'Times New Roman',"font.size": 16,"mathtext.fontset":'stix'}
rcParams.update(config)
# 读取数据
import pandas as pd
filename=r'F:/Rpython/lp37/testdata.xlsx'
df2=pd.read_excel(filename)#读取文件
x=df2['data1'].values
y=df2['data2'].values
xy = np.vstack([x,y])
z = gaussian_kde(xy)(xy)
idx = z.argsort()
x, y, z = x[idx], y[idx], z[idx]
fig,ax=plt.subplots(figsize=(12,9),dpi=100)
scatter=ax.scatter(x,y,marker='o',c=z,edgecolors='',s=15,label='LST',cmap='Spectral_r')
cbar=plt.colorbar(scatter,shrink=1,orientation='vertical',extend='both',pad=0.015,aspect=30,label='frequency') #orientation='horizontal'
font3={'family':'SimHei','size':16,'color':'k'}
plt.ylabel("估计值",fontdict=font3)
plt.xlabel("预测值",fontdict=font3)
plt.savefig('F:/Rpython/lp37/plot70.png',dpi=800,bbox_inches='tight',pad_inches=0)
plt.show()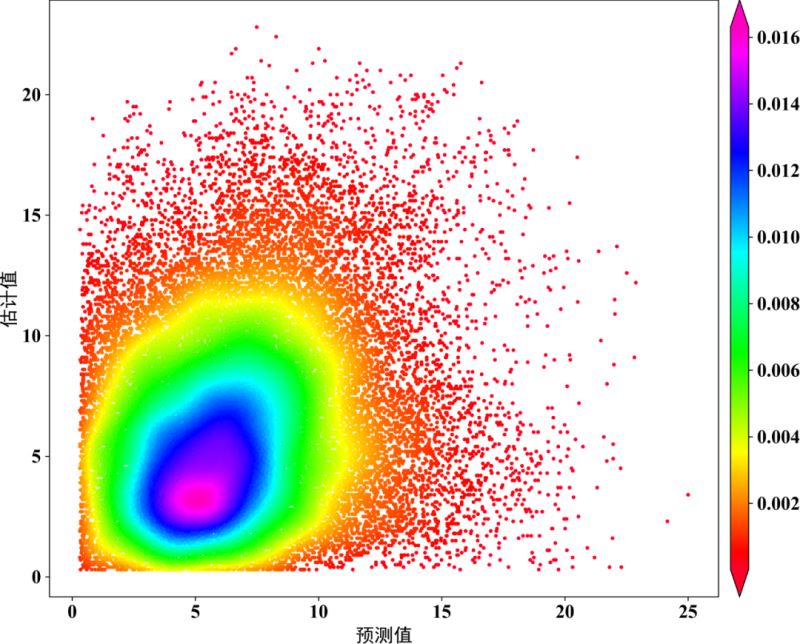
方式二
from statistics import mean
import matplotlib.pyplot as plt
from sklearn.metrics import explained_variance_score,r2_score,median_absolute_error,mean_squared_error,mean_absolute_error
from scipy import stats
import numpy as np
from matplotlib import rcParams
config = {"font.family":'Times New Roman',"font.size": 16,"mathtext.fontset":'stix'}
rcParams.update(config)
def scatter_out_1(x,y): ## x,y为两个需要做对比分析的两个量。
# ==========计算评价指标==========
BIAS = mean(x - y)
MSE = mean_squared_error(x, y)
RMSE = np.power(MSE, 0.5)
R2 = r2_score(x, y)
MAE = mean_absolute_error(x, y)
EV = explained_variance_score(x, y)
print('==========算法评价指标==========')
print('BIAS:', '%.3f' % (BIAS))
print('Explained Variance(EV):', '%.3f' % (EV))
print('Mean Absolute Error(MAE):', '%.3f' % (MAE))
print('Mean squared error(MSE):', '%.3f' % (MSE))
print('Root Mean Squard Error(RMSE):', '%.3f' % (RMSE))
print('R_squared:', '%.3f' % (R2))
# ===========Calculate the point density==========
xy = np.vstack([x, y])
z = stats.gaussian_kde(xy)(xy)
# ===========Sort the points by density, so that the densest points are plotted last===========
idx = z.argsort()
x, y, z = x[idx], y[idx], z[idx]
def best_fit_slope_and_intercept(xs, ys):
m = (((mean(xs) * mean(ys)) - mean(xs * ys)) / ((mean(xs) * mean(xs)) - mean(xs * xs)))
b = mean(ys) - m * mean(xs)
return m, b
m, b = best_fit_slope_and_intercept(x, y)
regression_line = []
for a in x:
regression_line.append((m * a) + b)
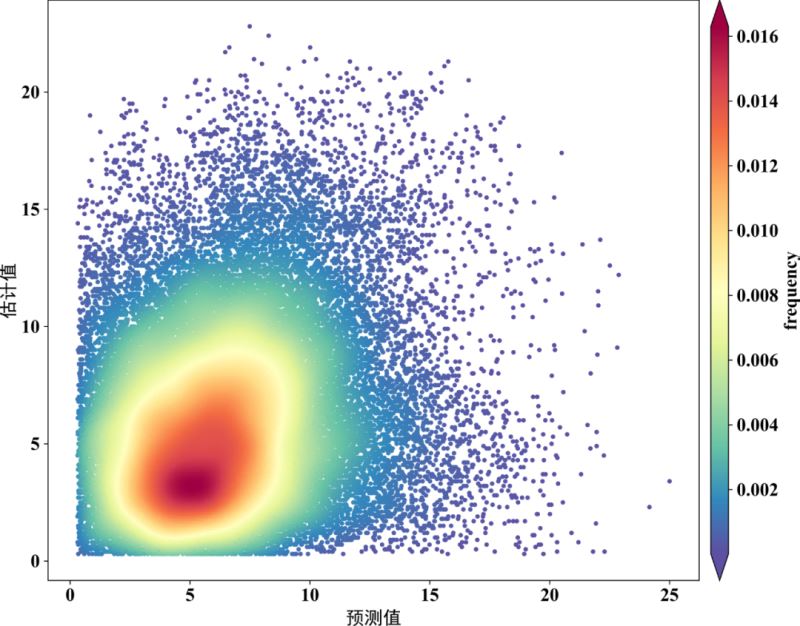
fig,ax=plt.subplots(figsize=(12,9),dpi=600)
scatter=ax.scatter(x,y,marker='o',c=z*100,edgecolors='',s=15,label='LST',cmap='Spectral_r')
cbar=plt.colorbar(scatter,shrink=1,orientation='vertical',extend='both',pad=0.015,aspect=30,label='frequency')
plt.plot([0,25],[0,25],'black',lw=1.5) # 画的1:1线,线的颜色为black,线宽为0.8
plt.plot(x,regression_line,'red',lw=1.5) # 预测与实测数据之间的回归线
plt.axis([0,25,0,25]) # 设置线的范围
plt.xlabel('OBS',family = 'Times New Roman')
plt.ylabel('PRE',family = 'Times New Roman')
plt.xticks(fontproperties='Times New Roman')
plt.yticks(fontproperties='Times New Roman')
plt.text(1,24, '$N=%.f$' % len(y), family = 'Times New Roman') # text的位置需要根据x,y的大小范围进行调整。
plt.text(1,23, '$R^2=%.3f$' % R2, family = 'Times New Roman')
plt.text(1,22, '$BIAS=%.4f$' % BIAS, family = 'Times New Roman')
plt.text(1,21, '$RMSE=%.3f$' % RMSE, family = 'Times New Roman')
plt.xlim(0,25) # 设置x坐标轴的显示范围
plt.ylim(0,25) # 设置y坐标轴的显示范围
plt.savefig('F:/Rpython/lp37/plot71.png',dpi=800,bbox_inches='tight',pad_inches=0)
plt.show()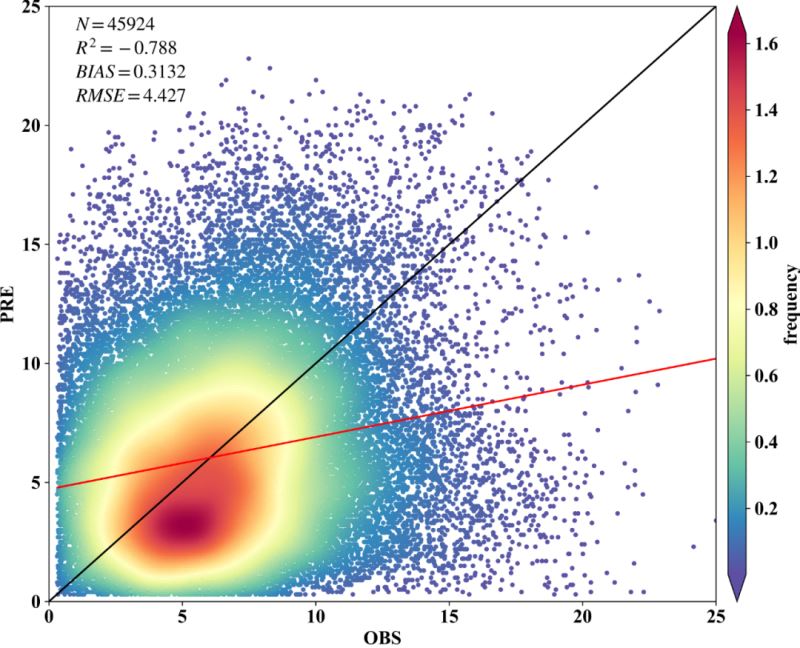
方式三
import pandas as pd
import numpy as np
from scipy import optimize
import matplotlib.pyplot as plt
from matplotlib import cm
from matplotlib.colors import Normalize
from scipy.stats import gaussian_kde
from matplotlib import rcParams
config={"font.family":'Times New Roman',"font.size":16,"mathtext.fontset":'stix'}
rcParams.update(config)
# 读取数据
filename=r'F:/Rpython/lp37/testdata.xlsx'
df2=pd.read_excel(filename)#读取文件
x=df2['data1'].values.ravel()
y=df2['data2'].values.ravel()
N = len(df2['data1'])
#绘制拟合线
x2 = np.linspace(-10,30)
y2 = x2
def f_1(x,A,B):
return A*x + B
A1,B1 = optimize.curve_fit(f_1,x,y)[0]
y3 = A1*x + B1
# Calculate the point density
xy = np.vstack([x,y])
z = gaussian_kde(xy)(xy)
norm = Normalize(vmin = np.min(z), vmax = np.max(z))
#开始绘图
fig,ax=plt.subplots(figsize=(12,9),dpi=600)
scatter=ax.scatter(x,y,marker='o',c=z*100,edgecolors='',s=15,label='LST',cmap='Spectral_r')
cbar=plt.colorbar(scatter,shrink=1,orientation='vertical',extend='both',pad=0.015,aspect=30,label='frequency')
cbar.ax.locator_params(nbins=8)
cbar.ax.set_yticklabels([0.005,0.010,0.015,0.020,0.025,0.030,0.035])#0,0.005,0.010,0.015,0.020,0.025,0.030,0.035
ax.plot(x2,y2,color='k',linewidth=1.5,linestyle='--')
ax.plot(x,y3,color='r',linewidth=2,linestyle='-')
fontdict1 = {"size":16,"color":"k",'family':'Times New Roman'}
ax.set_xlabel("PRE",fontdict=fontdict1)
ax.set_ylabel("OBS",fontdict=fontdict1)
# ax.grid(True)
ax.set_xlim((0,25))
ax.set_ylim((0,25))
ax.set_xticks(np.arange(0,25.1,step=5))
ax.set_yticks(np.arange(0,25.1,step=5))
plt.savefig('F:/Rpython/lp37/plot72.png',dpi=800,bbox_inches='tight',pad_inches=0)
plt.show()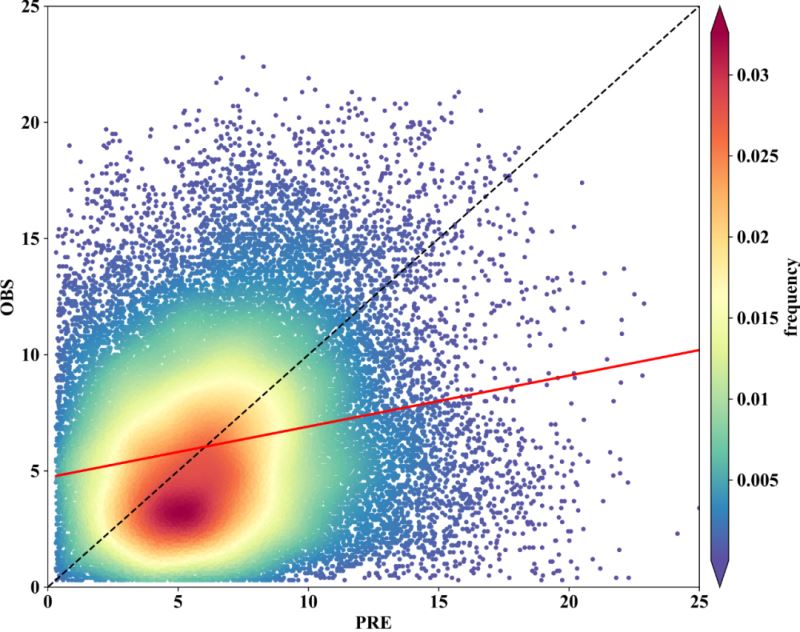

加载全部内容