Python期权定价
数量技术宅 人气:0期权是一种合约,它赋予买方在未来某个时间点以特定价格买卖资产的权利。 这些被称为衍生品的合约的交易有多种原因,但一种常见的用法是来对冲当资产价格以不利方式变动,所产生的风险敞口。
期权,即买入或卖出的权利,也是有价格的。 Black Scholes 模型描述了一种确定期权公平价格的方法,但还有许多其他方法可以确定价格。
期权,及其价值
欧式期权只有在未来达到预定日期(称为到期日)后才能使用(或行使),可以用字母 T 表示。
看涨期权赋予期权持有人以已知价格购买的权利。 如果资产的到期价格(用 ST 表示)高于执行价格 K ,则看涨期权会赚钱,否则就一文不值。
CT=max(0,ST−K)
同样,看跌期权是出售资产的权利。 当资产在到期日价格ST低于执行价格K时,看跌期权会赚钱,否则就一文不值。
PT=max(0,K−ST)
以下是到期时看跌期权和看涨期权的收益图。 我们的资产价格是 x 轴,收益是 y 轴。

风险中性估值
为了使用蒙特卡罗模拟为期权定价,我们使用风险中性估值,其中衍生品的公允价值是其未来收益的预期价值。
因此,在到期前的任何日期,用 t 表示,期权的价值是其到期收益预期的现值 T 。
Ct=PV(E[max(0,ST−K)])
Pt=PV(E[max(0,K−ST)])
在风险中性估值下,我们假设标的资产将平均获得无风险利率。 因此,要计算任何时间 t 的期权收益,我们要按该利率对收益进行贴现。 现在我们有一种计算现值 PV 的方法。

上面的公式中,除了St ,所有这些变量都是已知的,因此St是我们的模拟将提供的。
为了给期权定价,我们将创建一个模拟,为资产 St 最终价格提供许多观察结果。 通过平均所有的回报,我们得到了对回报的期望值。
模拟资产价格
Black Scholes 模型中使用的股票价格行为模型假设我们有一个已知的波动性,我们有一个无风险利率,并且资产的价格遵循几何布朗运动。
几何布朗运动是一个随机过程,其中随机变量的对数服从正态分布。 这种类型的过程通过对数正态分布来分配价格。
所以现在我们有一个计算时间 T 时刻资产价格的方法:
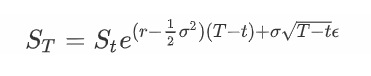
为此,我们需要知道:
r 是我们要贴现的无风险利率。 σ 是波动率,即股票回报的年化标准差。 (T-t) 给了我们年化的到期时间。 例如,对于 30 天选项,这将是 30/365=0.082... S 是在时间 t 标的资产的价格。 ϵ 是我们的随机值。 它的分布必须是标准正态(均值为 0.0,标准差为 1.0)
期权定价
为了在模拟过程中为期权定价,我们生成资产可能在到期时的许多价格,计算每个生成价格的期权收益,将它们平均,然后对最终价值进行贴现。
在创建完整模拟之前,我们将通过一个包含10次运行的小示例。假设我们有一个具有以下价值的资产:S = 100.00 美元和 σ = 20%,我们想为半年到期的看涨期权定价,执行价为 110.00 美元,我们的无风险利率是 1%。
| 随机变量 | 资产价格 | 收益 | 贴现收益 |
|---|---|---|---|
| 1.3620 | 120.64 | 10.64 | 10.58 |
| -0.7784 | 89.13 | 0.00 | 0.00 |
| -0.9408 | 87.11 | 0.00 | 0.00 |
| 0.2227 | 102.69 | 0.00 | 0.00 |
| -0.0364 | 98.99 | 0.00 | 0.00 |
| -1.4303 | 81.28 | 0.00 | 0.00 |
| -0.8306 | 88.47 | 0.00 | 0.00 |
| 1.5155 | 123.28 | 13.28 | 13.21 |
| -1.5679 | 79.71 | 0.00 | 0.00 |
| -1.6718 | 78.55 | 0.00 | 0.00 |
将折扣收益值平均,得出我们的看涨期权价格为 2.38 美元。 我们执行的模拟越多,价格就越准确。
现在我们可以看到模拟如何生成价格,让我们构建一个可以为期权定价的小型 Python 脚本,看看它是否与真实情况相符。 让我们看一下实际的例子。
为真实期权定价
在下图中,我们有一个谷歌看涨期权的报价,行使价为 860.00 美元,将于 2013 年 9 月 21 日到期。我们还可以看到它的最后交易价格是14.50 美元。这个例子给了我们尝试定价时,期权的一个目标价格。
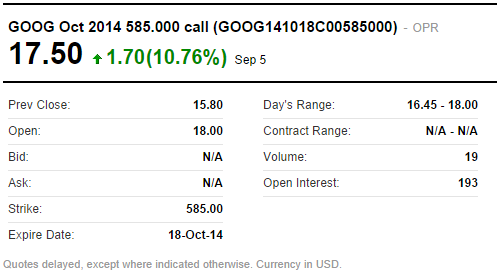
此处未指定的是波动性、无风险利率、当前的股票价格。 波动率是一个相当复杂的话题,因此就本文而言,我们将假设我们知道该特定期权的波动率为 20.76%。而股票当前价格可以通过查看各种来源找到,为857.29 美元。
对于无风险利率,我们可以使用与我们选择的到期时间相同的美国 LIBOR 利率; 我们的期权在大约三周后到期,由于没有三周利率,我们将使用两周利率来近似,即 0.14%。
接下来是Python代码的实现,首先我们将写下我们将如何生成资产价格。
def generate_asset_price(S,v,r,T):
return S * exp((r - 0.5 * v**2) * T + v * sqrt(T) * gauss(0,1.0))我们知道所有的输入值,所以我们可以像这样设定它们:
S = 857.29 # underlying price v = 0.2076 # vol of 20.76% r = 0.0014 # rate of 0.14% T = (datetime.date(2013,9,21) - datetime.date(2013,9,3)).days / 365.0 print generate_asset_price(S,v,r,T) >>> 862.1783726682384
现在我们需要能够计算这个生成价格的回报。 回想一下之前我们说过看涨期权在到期时价值是 ST-K 或 0,我们将其表示为一个函数,并应用于我们生成的资产价格。
def call_payoff(S_T, K):
return max(S_T - K, 0.0)
print call_payoff(862.18, 860)
>>> 2.1799999999完整的模拟
现在让我们将各模块代组合,并为 Google 期权定价。
import datetime
from random import gauss
from math import exp, sqrt
def generate_asset_price(S,v,r,T):
return S * exp((r - 0.5 * v**2) * T + v * sqrt(T) * gauss(0,1.0))
def call_payoff(S_T,K):
return max(0.0,S_T-K)
S = 857.29 # underlying price
v = 0.2076 # vol of 20.76%
r = 0.0014 # rate of 0.14%
T = (datetime.date(2013,9,21) - datetime.date(2013,9,3)).days / 365.0
K = 860.
simulations = 90000
payoffs = []
discount_factor = math.exp(-r * T)
for i in xrange(simulations):
S_T = generate_asset_price(S,v,r,T)
payoffs.append(
call_payoff(S_T, K)
)
price = discount_factor * (sum(payoffs) / float(simulations))
print 'Price: %.4f' % price程序运行结果如下,这与我们在市场上观察到的此 Google 期权的价格相匹配。
Price: 14.5069
需要注意的是,我们刚刚计算的谷歌期权实际上是一个美式期权,我们只是把它定价成欧式期权,没有考虑期权可以提前行权的可能性,尽管如此,我们仍然得出了正确的价格。
这是因为,非派息股票(例如文中举例的 Google)的美式看涨期权的价格与欧式看涨期权的价格相同。理论上,当股票不支付股息时,提前行权并不是最佳选择。 如果期权永远不会提前行权,那么美式期权的价格可以像欧式期权一样进行计算。
加载全部内容