C语言数据存储

时间:2022-06-03 耀星人气:0

前言

在计算机内存中，数据的存储方式都是以0和1的形式存储，也就是二进制的形式，数据是如何向内存写入的呢？整形数据以补码的形式存储，浮点型的存储规则较多，类似于科学计数法。

‍数据类型介绍

为什么需要有这些数据类型？

数据类型解决了数据存储的问题。

‍整形数据在内存中存储

整数中有三种二进制表示形式，分别是原码、反码、补码，正整数的原码 = 反码 = 补码，通常取最高位作为符号位。

原码：直接将正负整数按照二进制形式转换即可。

15原码: (0) 1111
-15原码: (1) 1111
23原码: (0) 10111
-28原码: (1) 11100
注意：()表示符号位,1表示负，0表示正。

补码：负整数的补码将原码的符号位不变，其它位依次取反。

15反码: (0) 1111
-15反码: (1) 0000
23反码: (0) 10111
-28反码: (1) 00011

反码：负整数的反码在补码的基础上+1

15补码: (0) 1111
-15补码: (1) 0001
23补码: (0) 11000
-28补码: (1) 00100

对于整形数据来说：数据存放的实际是存放补码。

当我们定义变量时，系统会根据变量的数据类型，给变量开辟空间。这也是为什么要引入数据类型这个概念。

1.举例：5是如何存储到内存中

5是一个整形常量，在C语言中写一个整形常量，不超过int类型所能表示的范围，以32位表示整形常量。

5的原码码 = 补码 = 反码

5原码：00000000 00000000 00000000 00000101

5存入short类型的变量：取后16位

00000000 00000000 00000000 00000101

5存入int类型的变量：取32位

00000000 00000000 00000000 00000101

2.举例：-10是如何存储到内存中的

-10原码：10000000 00000000 00000000 00001010

-10反码：11111111 11111111 11111111 11110101

-10补码：11111111 11111111 11111111 11110110

-10存入short类型：取后16位

11111111 11111111 11111111 11110110

-10存入int类型变量：取32位

11111111 11111111 11111111 11110110

如何取出数据？

取出数据首先要知道数据的地址，得到地址后，如何确定取出范围，由变量的数据类型来决定。

int main()
{
	/*
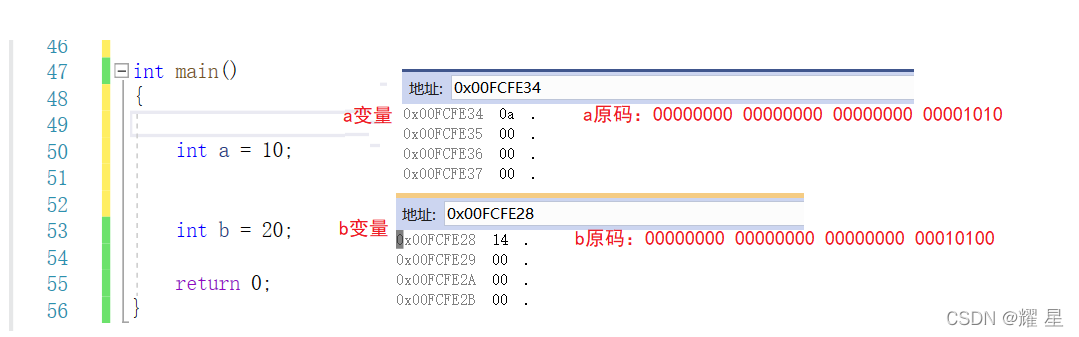
	a的原码、反码、补码：00000000 10011000 10010110 1000000
	*/
	int a = 10000000;
	/*
	b是short*类型，解引用访问时，只有访问两个字节的权限
	*b拿出的数据是补码： 10010110 10000000->原码：11101001 10000000
	*/
	short* b = &a;
	printf("%d", *b);//-27008
	return 0;
}

为什么要使用补码的形式存储？

在计算机中CPU有中，只有加法器。以补码形式存储，符号位参与运算，既可以计算减法也可以计算加法。

大端存储模式：指数据的低位保存在内存的高地址中，而数据的高位，保存在内存的低地址中。

小端存储模式：指数据的低位保存在内存的低地址中，而数据的高位，保存在内存的高地址中。

大小端主要由处理器决定，与编译器，操作系统这些没有直接的关系。

‍浮点型数据在内存存储

根据国际标准IEEE（电气和电子工程协会）754，任意一个二进制浮点数V可以表示成下面的形式：

(-1)S*M*2^E
(-1)S表示符号位，当S = 0，V为正数；S = -1，V为负数
M表示有效数值，大于等于1，小于2
2^E表示指数位

类似于科学计数法：1090 = 1.090*10^3

IEEE754规定单精度浮点型和双精度浮点型存储模型

IEEE 754对有效数字M和指数E，还有一些特别的规定。

1<=M<2，M可以写成1.xxxxxx的形式，xxxxxx表示小数部分。

IEEE754规定，在计算机内部保存M时，默认这个数的第一位总是1，因此可以舍去，只保存后面的xxxxxx部分。在读取时，再把第一位添上。节省一位有效数字.

对于指数E,情况比较多。

首先E为无符号整数，如果E为八位，取值范围时0~255，E为11位，取值范围为0~2047，但是再科学计数法中E可以出现负数，所以IEEE 754则规定，存入内存E的真实数必须加上一个中间数，对于八位的E，中间数为127，对于11位的E，中间数位1023。例如2^13的E是13，所以在保存E时，必须保存成13+127 = 140，即10001100。

指数E从内存中取出还可以分为3种情况

1.E不全为0或不全为1

这时浮点数就采用下面的规则表示，即指数E的计算值减去127（或1023），得到真实值，再将有效数字M前加上第一位的1。

比如：

0.5的二进制位0.1，由于规定整数部分1<=M<2，即第一位必须位1，则将小数点右移一位，则为1.0*2^(-1)，E的实际存储位-1+127，E的实际存储为01111110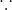，M = 1.0，小数部分为0，M的存储为23位00000000000000000000000。

则0.5的二进制表示形式位：

0 01111110 00000000 00000000 0000000

2.E全为0

这时，浮点数的指数E等于1-127（或者1-1023），即为真实值

有效数字M不再加上第一位的1，而是还原位0.xxxxxx的小数，这样可以表示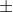0，以及接近于0的很小数字。

3.E全为1

如果有效数字M全位0，表示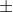无穷大。

举例：

10.0转化为二进制形式为1010.0，相当于：1.010*2^3，按照标准格式可得S = 0，M = 1.010，E = 3。

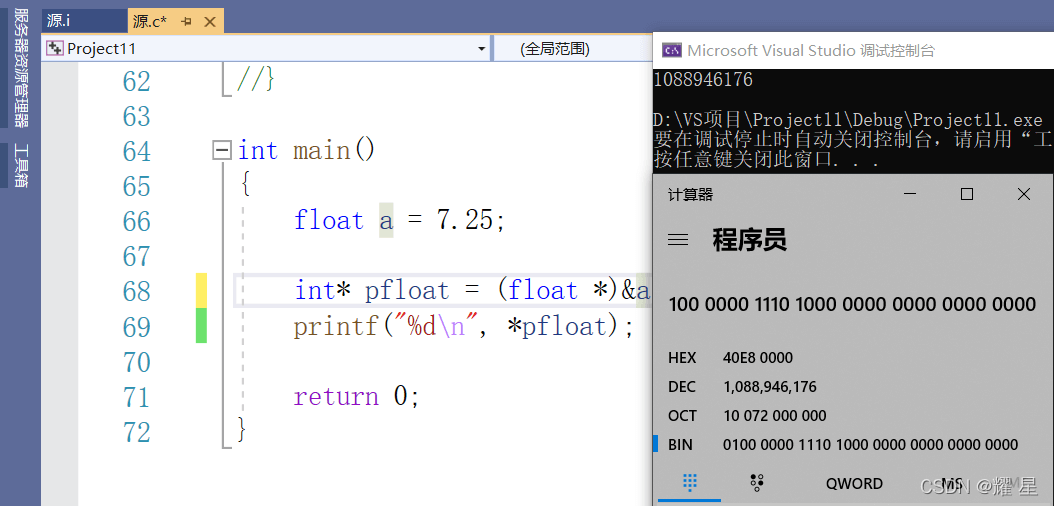
举例1：7.25是如何存储到内存中的呢？

首先将7.25转化为二进制111.01

写成标准形式：1.1101*2^2

S = 0，M = 1101，E = 2+127

0 10000001 11010000 00000000 0000000

验证：

有误的地方还请批评指正。

加载全部内容