C语言平衡二叉树

时间:2022-06-03 CodeWinter 人气:0

题目难度：简单

LeetCode链接：平衡二叉树

一、题目描述

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：一个二叉树每个节点的左右两个子树的高度差的绝对值不超过 1 。

二、解题思路

一棵二叉树是平衡二叉树，当且仅当其所有子树也都是平衡二叉树，因此我们使用递归的方式依次判断其所有子树是否为平衡二叉树，就知道这棵二叉树是不是平衡二叉树了。

自顶向下的递归（暴力解法）

自顶向下类似于前序遍历，先判断当前树是否平衡，再判断当前树的左右子树是否平衡。

核心思路

写两个函数：

子函数：计算当前任意一个节点(树) root 的高度 root 是空节点：Depth ( root ) = 0root 是非空节点：Depth ( root ) = max ( Depth ( root->left ) , Depth ( root->right ) ) + 1

主函数：依次递归遍历完 root 的所有子树，对于「当前遍历到的子树」，判断是否平衡，首先计算其左右子树的高度，然后判断高度差是否不超过 1

如果不超过，才能继续往下递归遍历「当前树的左右子树」，判断其是否平衡；
如果超过1，说明不满足平衡条件，则直接返回 false，不用往下递归了。

递归过程演示：自顶向下的递归类似于前序遍历

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
// 计算当前任意一个节点(树)的高度（子函数）
int TreeDepth(struct TreeNode* root)
{
    // 当前节点为空
    if(root == NULL)
    {
        return 0;
    }
    // 当前节点不为空，分别计算它的左右子树的高度
    int leftDepth = TreeDepth(root->left);
    int rightDepth = TreeDepth(root->right);
    // 当前节点(树)的高度
    return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
}
bool isBalanced(struct TreeNode* root){
    // 依次递归遍历完root的所有子树，分别判断当前子树是否为高度平衡二叉树
    // 当前树的根节点为空，说明其满足高度平衡的二叉树，返回true
    if(root == NULL)
    {
        return true;
    }
    // 当前树的根节点不为空，分别计算它左右子树的高度
    int leftDepth = TreeDepth(root->left);
    int rightDepth = TreeDepth(root->right);
    // 计算左右子树的高度差
    int ret = leftDepth > rightDepth ? leftDepth - rightDepth : rightDepth - leftDepth;
    // 高度差不超过1，才能继续往下递归遍历当前树的左右子树
    return ret <= 1 && isBalanced(root->left) && isBalanced(root->right);
}

复杂度分析：

时间复杂度：O(n2)，其中 n 是二叉树中的节点个数。

最坏情况下，二叉树是满二叉树，主函数 isBalanced(root) 需要遍历二叉树中的所有节点，时间复杂度是 O(n)。计算每个子树的最大高度函数 TreeDepth(root) 被重复调用。除了根节点，其余所有节点都会被遍历两次，复杂度为 O[2(n-1)]，所以时间复杂度为 n*2(n-1) ≈ n2。

空间复杂度：O(n)，其中 n 是二叉树中的节点个数。空间复杂度主要取决于递归调用的层数，递归调用的层数不会超过 n。

自底向上的递归（最优解法）

方法一自顶向下递归，类似前序遍历，先判断当前树是否平衡，再判断当前树的左右子树是否平衡，所以对于同一个节点，函数 TreeDepth 会被重复调用，会重复计算很多次子树的高度，导致时间复杂度较高。

如果使用自底向上的做法，则对于每个节点，函数 TreeDepth 只会被调用一次。因为到达左子树底部后，每次对应的左子树都是放在递归调度中的，每次只需要获取新的右子树长度便可。

自底向上递归类似于后序遍历，对于当前遍历到的节点，先递归地判断其左右子树是否平衡，再判断以当前节点为根的子树是否平衡。

如果当前树的左/右子树中只要有一个不平衡，则整个树就不平衡，返回-1（表示不平衡）
如果当前树是平衡的，则返回其高度，否则返回 -1（表示不平衡）。

写递归算法需要关注什么？

整个递归的终止条件：递归应该在什么时候结束？— 子树根节点为空的时候，空树也是平衡二叉树。
本级递归应该做什么？ — 判断当前树的左子树、右子树、以及当前树是否是平衡的。
返回值：应该返回给上一级的返回值是什么？— 当前树是平衡的，则返回其高度，不平衡则返回 -1。

递归算法流程：

每一级递归时，在我们眼中，当前树就是这样的，只有 root、left、right 三个节点。

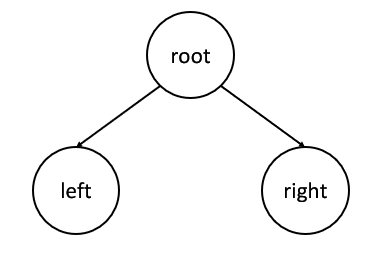
到叶子节点了，当前树根节点 root 为空，说明是平衡的，则返回高度 0；

当前树根节点 root 不为空，计算左右子树 left 和 right 的高度，并判断：

如果「左子树 left 高度为 -1」、或「右子树 right 高度为 -1」、或「左右子树高度差 > 1」，说明整个树不平衡，直接返回 -1（表示不平衡）。
如果不满足上面 3 种情况，说明当前树是平衡的，返回当前树的高度，即 max ( left, right ) + 1 。

补充：计算绝对值的函数：int abs( int n ); ，头文件 <stdlib.h> or <math.h>。

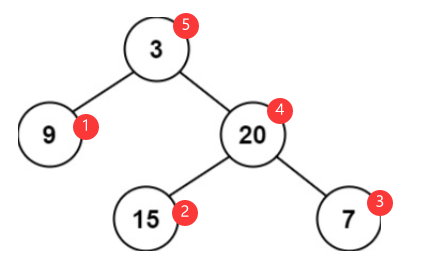
递归过程演示：自底向上递归类似于后序遍历

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
// 计算当前树的高度，并判断当前树是否是平衡二叉树
int _isBalanced(struct TreeNode* root)
{
    // 先分别判断当前树的左/右子树是否平衡
    // 如果当前树的左/右子树中只要有一个不平衡，则全树就不平衡，返回-1（表示不平衡）
    // 如果当前树的左右子树都平衡，则继续判断当前树是否平衡
    // 1. 到叶子节点了，当前树根节点为空，说明是平衡的，则返回高度0
    if(root == NULL)
    {
        return 0;
    }
    // 2. 当前树根节点不为空
    // 计算左右子树的高度
    int leftTreeDepth = _isBalanced(root->left);
    int rightTreeDepth = _isBalanced(root->right);
    // 不平衡的3种情况：左子树高度为-1，右子树高度为-1，左右子树高度差>1
    if(leftTreeDepth == -1 || rightTreeDepth == -1 || abs(leftTreeDepth - rightTreeDepth) > 1)
    {
        return -1;
    }
    // 如果不满足上面3种情况，说明当前树是平衡的，返回当前树的高度
    return leftTreeDepth > rightTreeDepth ? leftTreeDepth + 1 : rightTreeDepth + 1;
}
bool isBalanced(struct TreeNode* root){
    // 递归遍历过程中：
    // 只要有一个子树高度为-1，说明整个树是不平衡的，返回false
    // 所有子树高度都不等于-1，说明整个树是平衡的，返回true
    return _isBalanced(root) != -1;
}

复杂度分析：

1.时间复杂度：O(n)，其中 n 是二叉树中的节点个数。

最坏情况是二叉树为满二叉树时，需要遍历完满二叉树中的所有节点，自底向上方法，因此每个节点只会被遍历一次，所以时间复杂度是 O(n)。

2.空间复杂度：O(n)，其中 n 是二叉树中的节点个数。空间复杂度却决于递归调用的层数，有 n 个节点的二叉树为单边树时深度最大，为 n。

加载全部内容