python滑模控制
静候佳茵 人气:0上一篇文章介绍了Python使用OPENCV的目标跟踪算法实现自动视频标注效果,感兴趣的朋友点击查看,使用滑模变结构控制策略来解决汽车跟踪问题,今天通过本文介绍下python实现车辆跟随滑模控制的实例,内容如下所示:
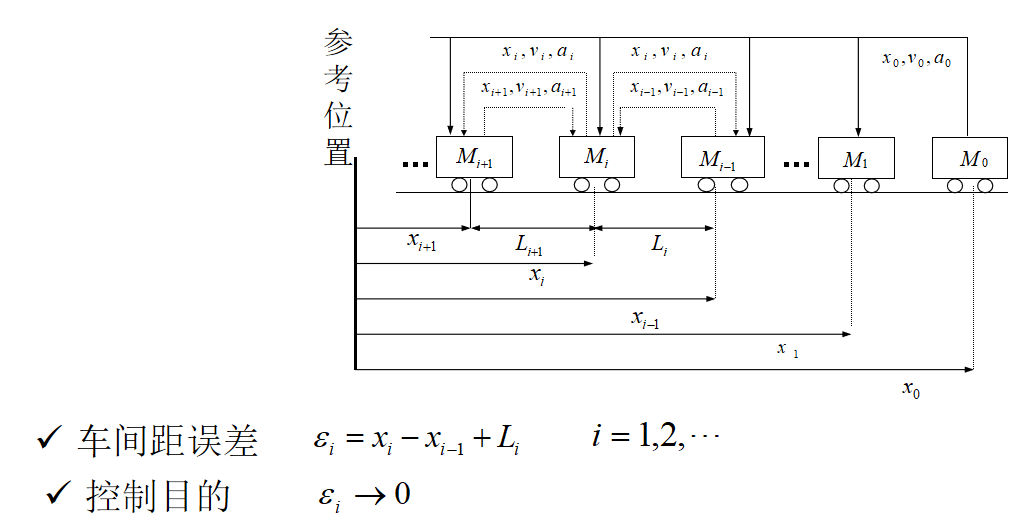
下面分别采用指数趋近律、等速趋近律、准滑模控制的方法完成车辆跟随问题的仿真
import matplotlib.pyplot as plt
'''
指数趋近律、等速趋近律、准滑模控制的车辆跟随问题仿真, 运行结果以图片形式保存在同目录下。
'''
# q1, q2分别是切换函数ei1, ei2前面的系数
q1, q2 = 2, 1
# lan是指数趋近律前面的系数
lan = 0.5
# 设定期望车间距均为12
l1, l2, l3, l4 = 12, 12, 12, 12
# 设定汽车质量均为1000
m1, m2, m3, m4 = 1000, 1000, 1000, 1000
# 设定动力学模型分子的速度平方项前的系数ci均为0.5(按照模型符号是负的)
c1, c2, c3, c4 = 0.5, 0.5, 0.5, 0.5
# 设定动力学模型分子的常数项系数Fi均为200(按照模型符号是负的)
f1, f2, f3, f4 = 200, 200, 200, 200
# 设定五辆车汽车的位移、速度、加速度
x0, x1, x2, x3, x4 = [100.], [90.], [79.5], [68.5], [57.]
v0, v1, v2, v3, v4 = [20.], [19.], [18.], [17.], [16.]
a1, a2, a3, a4 = [0.], [0.], [0.], [0.]
# 设定趋近律
def reaching_law(m:int , s:float, q2:int, mode='exponential'):
'''
mode: 指数趋近律exponential| 等速趋近律uniform| 准滑模控制quasi_sliding
'''
if mode == 'exponential':
return -m * lan * s / q2
if mode == 'uniform':
epslion = 0.3
if s > 0:
return -m * epslion / q2
if s == 0:
return 0
if s < 0:
return m * epslion / q2
if mode == 'quasi_sliding':
delta, epslion = 0.8, 2.
if s < -delta:
return m * epslion / q2
if s > delta:
return -m * epslion / q2
else:
return -m * epslion * s / (delta * q2)
# 设定第一辆车的加速度(分段函数), 要注意t的长度和a0的长度相等
def get_a0(t:list):
a0 = []
for i in t:
if i < 4:
a0.append(0)
continue
if i >= 4 and i < 7:
a0.append(-0.25*(i-4))
continue
if i >= 7 and i < 10:
a0.append(-0.75)
continue
if i >= 10 and i < 16:
a0.append(0.25*(i-10)-0.75)
continue
if i >= 16 and i < 19:
a0.append(0.75)
continue
if i >= 19 and i < 22:
a0.append(0.25*(19-i)+0.75)
continue
if i >= 22 and i <= 30: # 注意i=30, 所以是取两端, 故为301份
a0.append(0)
return a0
if __name__ == "__main__":
t = [float(i/10) for i in range(301)] # 将30秒划分成301份, [0, 0.1, 0.2, ..., 29.9, 30]
a0 = get_a0(t)
# 四辆车的车间距误差ei1列表
e11 = [x1[0] - x0[0] + l1]
e21 = [x2[0] - x1[0] + l2]
e31 = [x3[0] - x2[0] + l3]
e41 = [x4[0] - x3[0] + l4]
# 四辆车的车间距误差导数ei2的列表
e12 = [v1[0] - v0[0]]
e22 = [v2[0] - v1[0]]
e32 = [v3[0] - v2[0]]
e42 = [v4[0] - v3[0]]
# 四辆车切换函数的列表
s1 = [q1 * e11[0] + q2 * e12[0]]
s2 = [q1 * e21[0] + q2 * e22[0]]
s3 = [q1 * e31[0] + q2 * e32[0]]
s4 = [q1 * e41[0] + q2 * e42[0]]
# 四辆车控制律的列表
u1, u2, u3, u4 = [0], [0], [0], [0]
for i in range(1, 301):
# 最前车0的速度、加速度更新,可以看出更新时用了直线等效, 0.1指的是时间标度(列表t划分的, 也是之后绘图打印的x轴)
v0.append(v0[i-1] + 0.1 * (a0[i] + a0[i - 1]) * 0.5)
x0.append(x0[i-1] + 0.1 * (v0[i] + v0[i - 1]) * 0.5)
# 车1的车间距误差及导数更新
e11.append(x1[i-1] - x0[i-1]+l1)
e12.append(v1[i-1] - v0[i-1])
# 车1的切换函数更新
s1.append(q1 * e11[i] + q2 * e12[i])
# 等效控制
u1equ = c1 * (e12[i] + v0[i]) * (e12[i] + v0[i]) - m1 * q1 * e12[i] / q2 + m1 * a0[i] + f1
# 反馈控制(指数趋近律)
u1n = reaching_law(m1, s1[i], q2) # 默认采用指数趋近律, 下同
# u1n = reaching_law(m1, s1[i], q2, mode='uniform') # 采用等速趋近律
# u1n = reaching_law(m1, s1[i], q2, mode='quasi_sliding') # 采用准滑模控制
# 更新控制律
u1.append(u1equ + u1n)
# 利用控制律更新车1的加速度、速度、位移, 加速度是利用动力学模型得到的
a1.append((-c1 * v1[i-1] * v1[i-1] + u1[i] - f1) / m1)
v1.append(v1[i-1] + 0.1 * (a1[i] + a1[i - 1]) * 0.5)
x1.append(x1[i-1] + 0.1 * (v1[i] + v1[i - 1]) * 0.5)
# 车2、3、4过程同车1
e21.append(x2[i-1] - x1[i-1]+l2)
e22.append(v2[i-1] - v1[i-1])
s2.append(q1 * e21[i] + q2 * e22[i])
u2equ = c2 * (e22[i] + v1[i]) * (e22[i] + v1[i]) - m2 * q1 * e22[i] / q2 + m2 * a1[i] + f2
u2n = reaching_law(m2, s2[i], q2) # 默认采用指数趋近律
# u2n = reaching_law(m2, s2[i], q2, mode='uniform') # 采用等速趋近律
# u2n = reaching_law(m2, s2[i], q2, mode='quasi_sliding') # 采用准滑模控制
u2.append(u2equ + u2n)
a2.append((-c2 * v2[i-1] * v2[i-1] + u2[i] -f2) / m2)
v2.append(v2[i-1] + 0.1 * (a2[i] + a2[i - 1]) * 0.5)
x2.append(x2[i-1] + 0.1 * (v2[i] + v2[i - 1]) * 0.5)
e31.append(x3[i-1] - x2[i-1]+l3)
e32.append(v3[i-1] - v2[i-1])
s3.append(q1 * e31[i] + q2 * e32[i])
u3equ = c3 * (e32[i] + v2[i]) * (e32[i] + v2[i]) - m3 * q1 * e32[i] / q2 + m3 * a2[i] + f3
u3n = reaching_law(m3, s3[i], q2)
# u3n = reaching_law(m3, s3[i], q2, mode='uniform')
# u3n = reaching_law(m3, s3[i], q2, mode='quasi_sliding')
u3.append(u3equ + u3n)
a3.append((-c3 * v3[i-1] * v3[i-1] + u3[i] -f3) / m3)
v3.append(v3[i-1] + 0.1 * (a3[i] + a3[i - 1]) * 0.5)
x3.append(x3[i-1] + 0.1 * (v3[i] + v3[i - 1]) * 0.5)
e41.append(x4[i-1] - x3[i-1]+l4)
e42.append(v4[i-1] - v3[i-1])
s4.append(q1 * e41[i] + q2 * e42[i])
u4equ = c4 * (e42[i] + v3[i]) * (e42[i] + v3[i]) - m4 * q1 * e42[i] / q2 + m4 * a3[i] + f4
u4n = reaching_law(m4, s4[i], q2)
# u4n = reaching_law(m4, s4[i], q2, mode='uniform')
# u4n = reaching_law(m4, s4[i], q2, mode='quasi_sliding')
u4.append(u4equ + u4n)
a4.append((-c4 * v4[i-1] * v4[i-1] + u4[i] -f4) / m4)
v4.append(v4[i-1] + 0.1 * (a4[i] + a4[i - 1]) * 0.5)
x4.append(x4[i-1] + 0.1 * (v4[i] + v4[i - 1]) * 0.5)
# 开始绘图
# 绘制加速度曲线
plt.figure() # 设置画布
plt.plot(t, a0, label='car 0') # :是指绘制点划线
plt.plot(t, a1, label='car 1')
plt.plot(t, a2, label='car 2')
plt.plot(t, a3, label='car 3')
plt.plot(t, a4, label='car 4')
plt.xlabel("Time(s)",fontsize=13)
plt.ylabel("Acceleration(m/s^2)",fontsize=13)
plt.xlim(0, 30)
plt.legend()
plt.savefig('./acceleration.png') # 保存图像
# 绘制速度曲线
plt.clf() # 清空画布,不然会前后图像会重叠
plt.plot(t, v0, ':', label='car 0')
plt.plot(t, v1, ':', label='car 1')
plt.plot(t, v2, ':', label='car 2')
plt.plot(t, v3, ':', label='car 3')
plt.plot(t, v4, ':', label='car 4')
plt.xlabel("Time(s)",fontsize=13)
plt.ylabel("velocity(m/s)",fontsize=13)
plt.xlim(0, 30)
plt.legend()
plt.savefig('./velocity.png') # 保存图像
# 绘制位置曲线
plt.clf()
plt.plot(t, x0, ':', label='car 0')
plt.plot(t, x1, ':', label='car 1')
plt.plot(t, x2, ':', label='car 2')
plt.plot(t, x3, ':', label='car 3')
plt.plot(t, x4, ':', label='car 4')
plt.xlabel("Time(s)",fontsize=13)
plt.ylabel("position(m)",fontsize=13)
plt.xlim(0, 30)
plt.legend()
plt.savefig('./position.png')
# 绘制车间距误差ei1曲线
plt.clf()
plt.plot(t, e11, label='car 1')
plt.plot(t, e21, label='car 2')
plt.plot(t, e31, label='car 3')
plt.plot(t, e41, label='car 4')
plt.xlabel("Time(s)",fontsize=13)
plt.ylabel("space error(m)",fontsize=13)
plt.xlim(0, 30)
plt.legend()
plt.savefig('./space_error.png')
# 绘制车间距误差导数ei2曲线
plt.clf()
plt.plot(t, e12, ':', label='car 1')
plt.plot(t, e22, ':', label='car 2')
plt.plot(t, e32, ':', label='car 3')
plt.plot(t, e42, ':', label='car 4')
plt.xlabel("Time(s)",fontsize=13)
plt.ylabel("space_error_derivative(m)",fontsize=13)
plt.xlim(0, 30)
plt.legend()
plt.savefig('./space_error_derivative.png')
# 绘制切换函数曲线
plt.clf()
plt.plot(t, s1, label='car 1')
plt.plot(t, s2, label='car 2')
plt.plot(t, s3, label='car 3')
plt.plot(t, s4, label='car 4')
plt.xlabel("Time(s)",fontsize=13)
plt.ylabel("Switching Function",fontsize=13)
plt.xlim(0, 30)
plt.legend()
plt.savefig('./Switching_Function.png')
# 绘制控制输入U曲线
plt.clf()
plt.plot(t, u1, label='car 1')
plt.plot(t, u2, label='car 2')
plt.plot(t, u3, label='car 3')
plt.plot(t, u4, label='car 4')
plt.xlabel("Time(s)",fontsize=13)
plt.ylabel("Control Input",fontsize=13)
plt.xlim(0, 30)
plt.legend()
plt.savefig('./Control_Input.png')加载全部内容