python求解迷宫问题
不吃鱼的猫748 人气:0前言
在迷宫问题中,给定入口和出口,要求找到路径。本文将讨论三种求解方法,递归求解、回溯求解和队列求解。
在介绍具体算法之前,先考虑将迷宫数字化。这里将迷宫用一个二维的list存储(即list嵌套在list里),将不可到达的位置用1表示,可到达的位置用0表示,并将已经到过的位置用2表示。
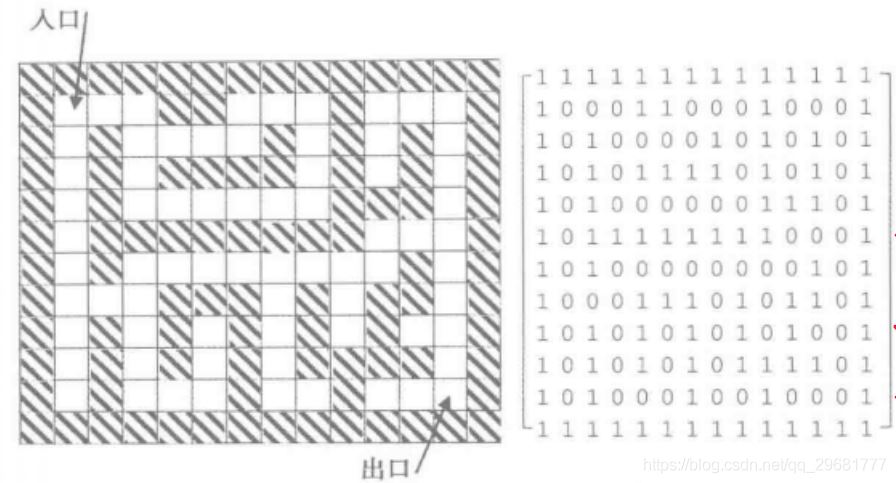
递归求解
递归求解的基本思路是:
- 每个时刻总有一个当前位置,开始时这个位置是迷宫人口。
- 如果当前位置就是出口,问题已解决。
- 否则,如果从当前位置己无路可走,当前的探查失败,回退一步。
- 取一个可行相邻位置用同样方式探查,如果从那里可以找到通往出口的路径,那么从当前位置到出口的路径也就找到了。
在整个计算开始时,把迷宫的人口(序对)作为检查的当前位置,算法过程就是:
- mark当前位置。
- 检查当前位置是否为出口,如果是则成功结束。
- 逐个检查当前位置的四邻是否可以通达出口(递归调用自身)。
- 如果对四邻的探索都失败,报告失败。
dirs=[(0,1),(1,0),(0,-1),(-1,0)] #当前位置四个方向的偏移量
path=[] #存找到的路径
def mark(maze,pos): #给迷宫maze的位置pos标"2"表示“倒过了”
maze[pos[0]][pos[1]]=2
def passable(maze,pos): #检查迷宫maze的位置pos是否可通行
return maze[pos[0]][pos[1]]==0
def find_path(maze,pos,end):
mark(maze,pos)
if pos==end:
print(pos,end=" ") #已到达出口,输出这个位置。成功结束
path.append(pos)
return True
for i in range(4): #否则按四个方向顺序检查
nextp=pos[0]+dirs[i][0],pos[1]+dirs[i][1]
#考虑下一个可能方向
if passable(maze,nextp): #不可行的相邻位置不管
if find_path(maze,nextp,end):#如果从nextp可达出口,输出这个位置,成功结束
print(pos,end=" ")
path.append(pos)
return True
return False
def see_path(maze,path): #使寻找到的路径可视化
for i,p in enumerate(path):
if i==0:
maze[p[0]][p[1]] ="E"
elif i==len(path)-1:
maze[p[0]][p[1]]="S"
else:
maze[p[0]][p[1]] =3
print("\n")
for r in maze:
for c in r:
if c==3:
print('\033[0;31m'+"*"+" "+'\033[0m',end="")
elif c=="S" or c=="E":
print('\033[0;34m'+c+" " + '\033[0m', end="")
elif c==2:
print('\033[0;32m'+"#"+" "+'\033[0m',end="")
elif c==1:
print('\033[0;;40m'+" "*2+'\033[0m',end="")
else:
print(" "*2,end="")
print()
if __name__ == '__main__':
maze=[[1,1,1,1,1,1,1,1,1,1,1,1,1,1],\
[1,0,0,0,1,1,0,0,0,1,0,0,0,1],\
[1,0,1,0,0,0,0,1,0,1,0,1,0,1],\
[1,0,1,0,1,1,1,1,0,1,0,1,0,1],\
[1,0,1,0,0,0,0,0,0,1,1,1,0,1],\
[1,0,1,1,1,1,1,1,1,1,0,0,0,1],\
[1,0,1,0,0,0,0,0,0,0,0,1,0,1],\
[1,0,0,0,1,1,1,0,1,0,1,1,0,1],\
[1,0,1,0,1,0,1,0,1,0,1,0,0,1],\
[1,0,1,0,1,0,1,0,1,1,1,1,0,1],\
[1,0,1,0,0,0,1,0,0,1,0,0,0,1],\
[1,1,1,1,1,1,1,1,1,1,1,1,1,1]]
start=(1,1)
end=(10,12)
find_path(maze,start,end)
see_path(maze,path)代码中see_path函数可以在控制台直观打印出找到的路径,打印结果如下:

S是入口位置 ,E是出口位置,*代表找到的路径,#代表探索过的路径。
回溯求解
在回溯解法中,主要是用栈来存储可以探索的位置。利用栈后进先出的特点,在一条分路上探索失败时,回到最近一次存储的可探索位置。这是一种深度优先搜索的方法。
def maze_solver(maze,start,end):
if start==end:
print(start)
return
st=SStack()
mark(maze,start)
st.push((start,0)) #入口和方向0的序对入栈
while not st.is_empty(): #走不通时回退
pos,nxt=st.pop() #取栈顶及其检查方向
for i in range(nxt,4): #依次检查未检查方向,算出下一位置
nextp = pos[0] + dirs[i][0], pos[1] + dirs[i][1]
if nextp==end:
print_path(end,pos,st) #到达出口,打印位置
return
if passable(maze,nextp): #遇到未探索的新位置
st.push((pos,i+1)) #原位置和下一方向入栈
mark(maze,nextp)
st.push((nextp,0)) #新位置入栈
break #退出内层循环,下次迭代将以新栈顶作为当前位置继续
print("找不到路径")队列求解
队列求解算法中,以队列存储可以探索的位置。利用队列先进先出的特点,实现在每个分支上同时进行搜索路径,直到找到出口。这是一种广度优先搜索的方法。
def maze_solver_queue(maze,start,end):
path.append(start)
if start==end:
print("找到路径")
return
qu=SQueue()
mark(maze,start)
qu.enqueue(start) #start位置入队
while not qu.is_empty(): #还有候选位置
pos=qu.dequeue() #取出下一位置
for i in range(4): #检查每个方向
nextp = pos[0] + dirs[i][0], pos[1] + dirs[i][1]
if passable(maze,nextp): #找到新的探索方向
if nextp==end: #是出口,成功
print("找到路径")
path.append(end)
return
mark(maze,nextp)
qu.enqueue(nextp) #新位置入队
path.append(nextp)
print("未找到路径")但队列求解方法,不能直接得出找到的具体路径,要得到找到的路径还需要其他存储结构(如链表)。
总结
加载全部内容