C语言二分查找

时间:2022-05-28 枫叶人气:0

前篇文章聊到了二分查找的基础以及细节的处理问题，主要介绍了查找和目标值相等的元素、查找第一个和目标值相等的元素、查找最后一个和目标值相等的元素三种情况。

这些情况都适用于有序数组中查找指定元素这个基本的场景，但实际应用中可能不会这么直接，甚至看了题目之后，都不会想到可以用二分查找算法来解决。

本文就来分析下二分查找在实际中的应用，通过分析几个应用二分查找的实例，总结下能使用二分查找算法的一些共同点，以后大家遇到相关的实际问题时，能有一个基本的分析方法，不至于一点儿头绪也没有。

基础的二分查

找先来回顾下基础的二分查找的基本框架，一般实际场景都是查找和 target 相等的最左侧的元素或者最右侧的元素，代码如下：

查找左侧边界

int binary_search_firstequal(vector<int> &vec, int target)
{
    int ilen = (int)vec.size();
    if(ilen <= 0) return -1;
    int left = 0;
    int right = ilen - 1;
    while (left <= right)
    {
        int mid = left + (right - left) / 2;
        //找到了目标,继续向左查找目标
        if (target == vec[mid]) right = mid - 1;
        else if(target < vec[mid]) right = mid -1;
        else left = mid + 1;        
    }
    if(right + 1 < ilen && vec[right + 1] == target) return right+1;
    return -1;
}

查找右侧边界

int binary_search_lastequal(vector<int> &vec, int target)
{
    int ilen = (int)vec.size();
    if(ilen <= 0) return -1;
    int left = 0;
    int right = ilen - 1;
    while (left <= right)
    {
        int mid = left + (right - left) / 2;
        //找到了目标，继续向右查找目标
        if (target == vec[mid]) left = mid + 1;
        else if(target < vec[mid]) right = mid -1;
        else left = mid + 1;        
    }
    if(left - 1 < ilen && vec[left - 1] == target) return left - 1;
    return -1;
}

二分查找问题分析

二分查找问题的关键是找到一个单调关系，单调递增或者单调递减。

我们把二分查找的代码简化下：

int target;             // 要查找的目标值
vector<int> vec;        // 数组
int left = 0;           // 数组起始索引
int right = ilen - 1;   // 数组结束索引
while (left <= right)   // 查找 target 位于数组中的索引
{
   int mid = left + (right - left) / 2;
   if (target == vec[mid]) return mid;
}

上面的二分查找的单调关系是什么呢 ?是数组的索引和索引处元素的值，索引越大，元素的值越大，用伪代码表示形式如下：

int func(vector<int>&vec,int index)
{
    return vec[index];
}
int search(vector<int>&vec,int target)
{
  while (left <= right)
  {
     int mid = left + (right - left) / 2;
     if (target == func(vec,mid))
     {
         ....
     }
     else if(target > func(vec,mid))
     {
         ...
     }
     else
     {
         ...
     }
  }
}

上述伪代码中，我们把单调关系用一个函数 func 来表示，传入参数是数组以及数组索引，函数返回数组指定索引处的元素。

在二分查找的 while 循环中 target 直接和 func 函数的返回值进行比较。

听起来有些抽象，我们直接从 leetcode 上选几道题来分析下。

实例1: 爱吃香蕉的珂珂

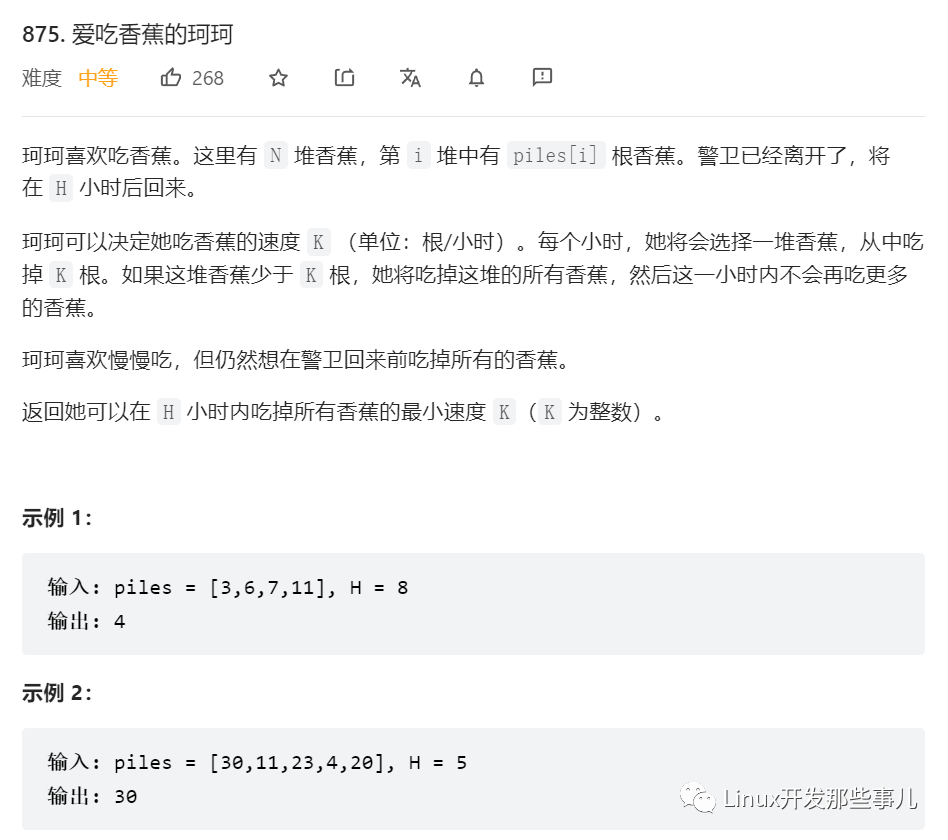
从题目的描述，跟有序数组完全不搭边，所以初看这道题，根本想不到用二分查找的方法去分析。

如果看完题目，没有任何思路的话，可以缕一缕题目涉及到的条件，看能否分析出一些有用的点。

题意分析
珂珂要吃香蕉，面前摆了 N 堆，一堆一堆地吃
珂珂 1 小时能吃 K 根，但如果一堆少于 K 根，那也得花一小时
如果 1 堆大于 K 根，那么超过 K 的部分也算 1 小时
问：只给 H 小时，珂珂要吃多慢(K 多小)，才能充分占用这 H 小时

一般题目的问题是什么，单调关系就跟什么有关，根据题意可知：珂珂吃香蕉的速度越小，耗时越多。反之，速度越大，耗时越少，这就是题目的单调关系。

我们要找的是速度, 因为题目限制了珂珂一个小时之内只能选择一堆香蕉吃，因此速度最大值就是这几堆香蕉中，数量最多的那一堆, 最小速度毫无疑问是 1 了，最大速度可以通过轮询数组获得。

int maxspeed = 1;
for(auto &elem : vec)
{
    if(elem > maxspeed) maxspeed = elem;
}+

又因为珂珂一个小时之内只能选择一堆香蕉吃，因此，每堆香蕉吃完的耗时 = 这堆香蕉的数量 / 珂珂一小时吃香蕉的数量。根据题意，这里的 / 在不能整除的时候，还需要花费 1 小时吃完剩下的，所以吃完一堆香蕉花费的时间，可以表示成。

hour = piles[i] / speed;
if(0 != piles[i] % speed) hour += 1;

香蕉的堆数以及每堆的数量是确定的，要在 H 小时内吃完，时间是输入参数，也是确定的了，现在唯一不确定的就是吃香蕉的速度，我们需要做的就是在最小速度到最大速度之间找出一个速度，使得刚好能在 H 小时内吃完香蕉。

前面说到吃香蕉的速度和吃完香蕉需要的时间之间是单调关系，我们先把单调关系的函数定义出来。

// 速度为 speed 时，吃完所有堆的食物需要多少小时
int eatingHour(vector<int>&piles,int speed)
{
    if(speed <= 0) return -1;
    int hour = 0;
    for(auto &iter : piles)
    {
        hour += iter / speed;
        if(0 != iter % speed) hour += 1;
    }
    return hour;
}

题目要求吃完香蕉的最小速度，也就是速度要足够小，小到刚好在 H 小时内吃完所有的香蕉，所以是求速度的左侧边界。

好了，分析完之后，写出代码:

int minEatingSpeed(vector<int> &piles, int h)
{
    //1小时最多能吃多少根香蕉
    int maxcount = 1;
    for (auto &iter : piles)
    {
        if (maxcount < iter) maxcount = iter; 
    }
    //时间的校验
    if (h < 1 || h < (int)piles.size() )  return -1;
    int l_speed = 1;
    int r_speed = maxcount;
    while (l_speed <= r_speed)
    {
        int m = l_speed + (r_speed - l_speed) / 2;
        // eatingHour 函数代码见上文
        int hours = eatingHour(piles, m);
        if (hours == h)
        {
            // 求速度的左侧边界
            r_speed = m - 1;
        }
        else if (hours < h)
        {
            // hours 比 h 小，表示速度过大，边界需要往左边移动
            r_speed = m - 1;
        }
        else
        {
            // hours 比 h 大，表示速度国小，边界需要往右边移动
            l_speed = m + 1;
        }
    }
    return l_speed;
}

上述代码中，我们列出了 while 循环中的 if 的所有分支，是为了帮助理解的，大家可自行进行合并。

实例2：运送包裹

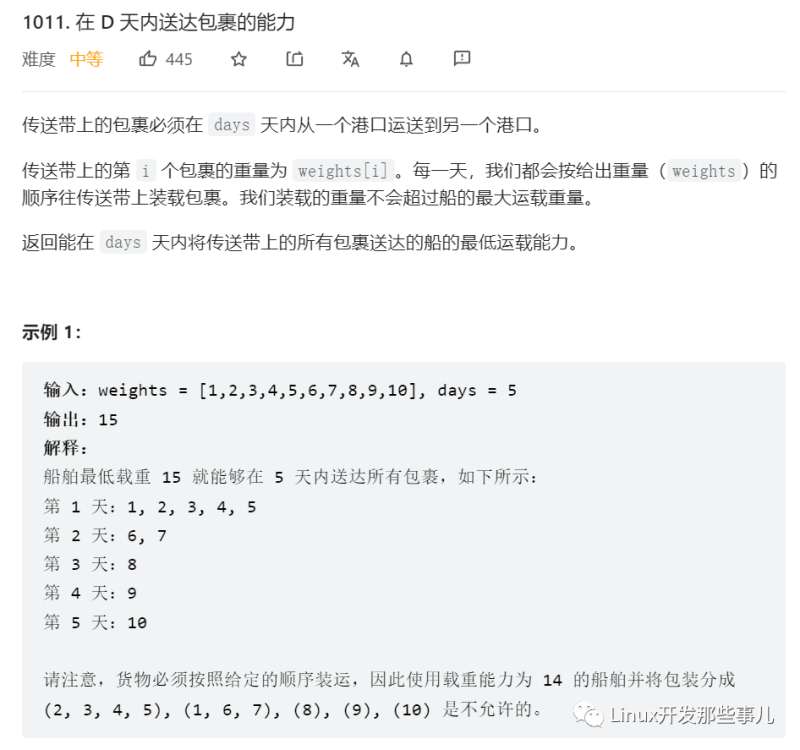
题目要求船的运载能力, 船的运载能力和运输需要的天数成反比，运载能力越大，需要的天数越少，运载能力越小，需要的天数越多，也即存在单调关系，下面定义出单调关系的函数。

//船的载重为 capcity 时,运载 weights 货物需要多少天
int shipDays(const vector<int> &weights, int capacity)
{
    //船载重校验
    if(capacity <= 0) return -1;
    int isize = (int)weights.size();
    int temp = 0;
    int days = 0;
    for(int i = 0; i < isize; ++i)
    {
        if(temp + weights[i] <= capacity)
        {
            temp += weights[i];
            continue;
        }
        ++days;
        temp = weights[i];
    }
    //还有剩余的，需要额外在运送一趟
    if(temp > 0)  ++days;
    return days;
}

题目中隐含的几个信息：

船的最小载重需要大于等于传送带上最重包裹的重量，因为每次至少要装载一个包裹
船的最大载重等于传送带上所有包裹的总重量，也即所有的包裹可以一次全部装上船
船每天只能运送一趟包裹

确定了船的运载范围后，相当于确定了二分查找的区间，另外，题目求的是船的最小运载能力，相当于求运载能力的左侧边界。

分析到这里，就可以写出基本的查找框架了，这里直接给出代码了。

int shipWithinDays(vector<int> &weights, int days)
{
    int isize = (int)weights.size();
    if (isize <= 0) return 0;
    //最小载重,需要等于货物的最大重量
    int mincapacity = 0;
    //最大载重，全部货物重量的总和
    int maxcapacity = 0;
    for (auto &iter : weights)
    {
        maxcapacity += iter;
        if (iter > mincapacity)
        {
            mincapacity = iter;
        }
    }
    int l = mincapacity;
    int r = maxcapacity;
    while (l < r)
    {
        int m = l + (r - l) / 2;
        int d = shipDays(weights, m);
        if (d == days)
        {
            r = m - 1;
        }
        else if (d < days)
        {
            // d 比 days 小，表示船载重太大，载重边界需要往左移
            r = m - 1;
        }
        else
        {
            // d 比 days 大，表示船载重太小，载重边界需要往右移
            l = m + 1;
        }
    }
    return l;
}

小结总结来说，如果发现题目中存在单调关系，就可以尝试使用二分查找的思路来解决，分析单调关系，写出单调函数，搞清楚二分查找的范围，确定查找的代码框架，再进行边界细化，就能够写出最终代码。

加载全部内容