Java 求和
Scintillator. / 人气:0今天遇到了这样一个题

题目说了不能用算数运算符,那么我们就只能从 逻辑运算符 和 移位运算符 入手了。
我们知道 ^ (异或)操作是对两个数进行无进位求和,如果两个数相加本来就不产生进位,那么该和就是两数之和。 这就是解题的关键所在。一般来说,两数相加是会产生进位的,而要得到正确的和,应该是在 “无进位之和” 的基础上加上进位,那我们首先应该得到进位。我们知道,当两个数对应位置都为1的情况下,才会有进位的产生,即对应位置 A&B==1的条件下,就可以得到每一位的进位,但是进位是将这个1加到对应的更高一位,所以我们将得到的进位整体进行左移一位,再和之前得到的 “无进位之和” 相加,就可以得到两数之和。
我们发现这里就可以无限套娃了,要得到 “无进位之和” 和 “产生的进位” 之和,那么将这两个数再分别看做新的两个数,对其求和。也是重复之前的操作,直到两数不能产生进位,就可以直接通过 ^ 运算得到结果。
假设我们求 23 + 16 的值
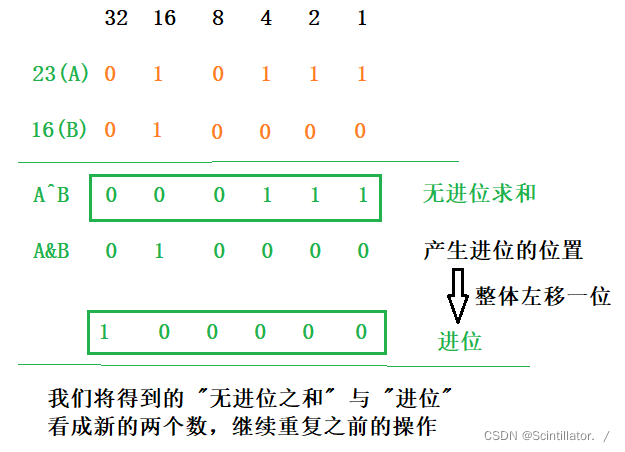
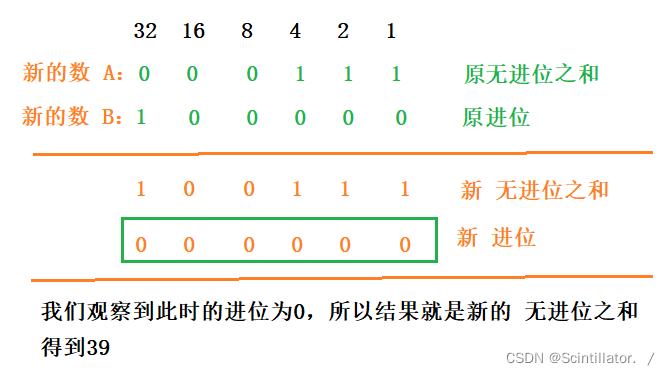
根据上述思路,我们很容易就可以写出代码
public static int addAB(int A, int B) {
// 当两数的产生的进位为 0,就退出循环,返回其无进位和,就是结果
while ((A & B) != 0) {
int A_B = A ^ B;// 无进位求和
int AB = (A & B) << 1;// 得到进位
// 接下来就是求 得到的进位 + 无进位之和,重复前面的操作,直到不产生进位
A = A_B;
B = AB;
}
// 最后返回新的无进位之和
return (A ^ B);
}
那么为了验证它的正确性,我们这里使用对数器,将该函数与 ’ + ’ 运算符比较。
public static void main(String[] args) {
int count = 1_0000_0000;// 比较次数 100000000次
Random random = new Random();// 生成随机数字
boolean flag = true;// 相等则为 true
for (int i = 0; i < count; i++) {
int num1 = random.nextInt(Integer.MAX_VALUE/2);// 随机正数1
int num1_2 = random.nextInt(Integer.MAX_VALUE/2);// 随机正数2
// 随机正数1 + 随机正数2
if ((num1+num1_2) != addAB(num1,num1_2)){
// 有一次不相等的,则退出循环
flag = false;
break;
}
int num2 = -random.nextInt(Integer.MAX_VALUE/2);// 随机负数1
int num2_2 = -random.nextInt(Integer.MAX_VALUE/2);// 随机负数2
// 随机负数1 + 随机负数2
if ((num2+num2_2) != addAB(num2,num2_2)){
// 有一次不相等的,则退出循环
flag = false;
break;
}
int num3 = random.nextInt(Integer.MAX_VALUE);// 随机正数
int num4 = -random.nextInt(Integer.MAX_VALUE);// 随机负数
// 随机正数 + 随机负数
if ((num3+num4) != addAB(num3,num4)){
// 有一次不相等的,则退出循环
flag = false;
break;
}
}
System.out.println(flag);
}
运行结果:
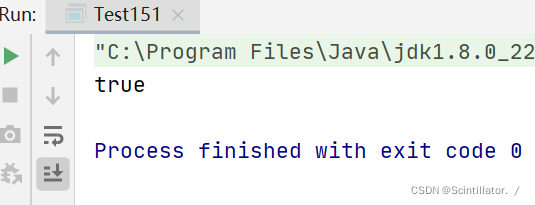
最后输出结果为 true ,说明我们计算随机产生的 正数+正数、负数+负数、正数+负数 分别100000000次,没有一次出错,说明该函数可靠。
加载全部内容