go归并排序算法

今天继续基础排序算法的图解和Go 代码实现，这次分享一个时间复杂度为*** 诶，时间复杂度多少先保密，文末会有分析。这次分享的排序算法是—归并排序(Merge Sort)。

归并排序的思想

与快速排序一样，归并排序采用的也是分治的策略，把原本的问题先分解成一些小问题进行求解，再把这些小问题各自的答案修整到一起得到原本问题的答案，从而达到分而治之的目的。

归并排序算法会把要排序的序列分成长度相当的两个子序列，当分无可分每个子序列中只有一个数据的时候，就对子序列进行归并。

归并指的是把两个排序好的子序列合并成一个有序序列。该操作会一直重复执行，直到所有子序列归并为一个整体为止。

归并排序的过程下面我们依然用图例过一遍归并排序对一个序列进行排序的过程。

图例出自—《我的第一本算法书》

首先，假设有下面这样一个待排序的序列：

待排序的一串数字

将序列以对半分割的形式分成两段。

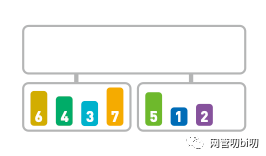
把序列二分成两段

再继续对子序列进行对半分割，分解下去。

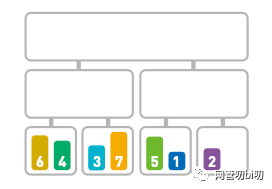
再继续往下分

直到分无可分，每个子序列中只有一个数据。

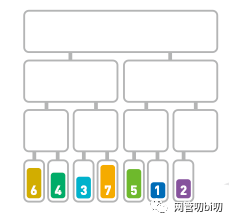
分解到每个子序列只有一个数据

接下来对分割后的数据进行合并，合并时需要将数字按从小到大的顺序排列。

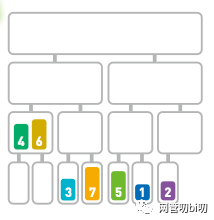
合并序列时按大小排序

把 6 和 4 合并，合并时按照数字大小排序，合并后的顺序为【4，6】，接下来把 3 和 7 合并，合并后的顺序为【3，7】。

[继续按照大小顺序合并后面的序列]。

下面，我们看看怎么合并【4，6】和【3，7】这两个序列。合并这种含有多个数字的子序列时，要先比较首位数字，再移动较小的数字。

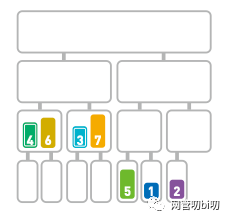
合并多元素的序列时，从首位开始比较，小的先移动

这里要比较两个子序列的首位数字是4 和 3。由于 4 > 3，所以合并序列时先移动 3。

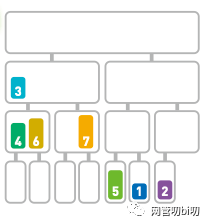
4 > 3，所以合并序列时先移动 3

接下来，再按照比较两个序列首位，小的先合并，大的留下来继续比较的规则合并两个序列。

4 小于 7，所以先移动 4 到合并的序列。

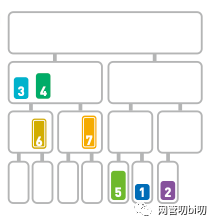
由于4<7，所以移动4

两个子序列剩下的元素中，6 小于 7，所以先移动 6。

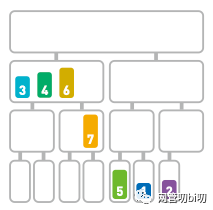
6 < 7 所以先移动 6

最后移动剩下的 7。

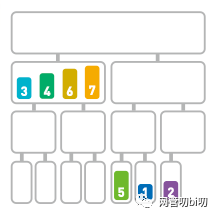
子序列最后剩下了7，合并到序列中去

递归执行上面的操作，直到所有的数字都合并到一个整体的序列上为止。

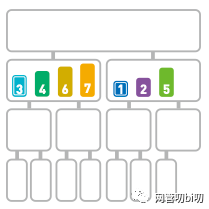
小序列合并成两个大的序列

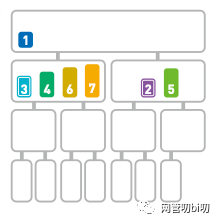
再继续往完整的序列上合并

最后得到一个完整的排序完成的序列 。

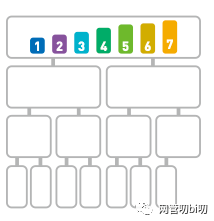
排序完成的序列

归并排序的 Go 代码实现

下面上一个用归并排序的Go代码实现，代码很简单，实现步骤就都放在了代码的注释里，就不再多说啦，先收藏文章(也要记得点赞)，等有时间了自己在电脑上运行一下试试吧。

package main
import "fmt"
// 自顶向下归并排序，排序范围在 [begin,end) 的数组
func MergeSort(array []int, begin int, end int) {
    // 元素数量大于1时才进入递归
    if end - begin > 1 {
        // 将数组一分为二，分为 array[begin,mid) 和 array[mid,high)
        mid := begin + (end-begin+1)/2
        // 先将左边排序好
        MergeSort(array, begin, mid)
        // 再将右边排序好
        MergeSort(array, mid, end)
        // 两个有序数组进行合并
        merge(array, begin, mid, end)
    }
}
// 归并操作
func merge(array []int, begin int, mid int, end int) {
    // 申请额外的空间来合并两个有序数组，这两个数组是 array[begin,mid),array[mid,end)
    leftSize := mid - begin         // 左边数组的长度
    rightSize := end - mid          // 右边数组的长度
    newSize := leftSize + rightSize // 辅助数组的长度
    result := make([]int, 0, newSize)
    l, r := 0, 0
    for l < leftSize && r < rightSize {
        lValue := array[begin+l] // 左边数组的元素
        rValue := array[mid+r]   // 右边数组的元素
        // 小的元素先放进辅助数组里
        if lValue < rValue {
            result = append(result, lValue)
            l++
        } else {
            result = append(result, rValue)
            r++
        }
    // 将剩下的元素追加到辅助数组后面
    result = append(result, array[begin+l:mid]...)
    result = append(result, array[mid+r:end]...)
    // 将辅助数组的元素复制回原数组，这样该辅助空间就可以被释放掉
    for i := 0; i < newSize; i++ {
        array[begin+i] = result[i]
    return

归并排序的时间复杂度

老规矩，看完算法思想和实现步骤后，我们再来分析一下归并排序算法的时间复杂度。

归并排序中，分割序列所花费的时间不算在运行时间内 (可以当作序列本来就是分 割好的)。在合并两个已排好序的子序列时，只需依次比较处在序列首位数据的大小，然后移动较小的数据，因此只需花费和两个子序列的长度相应的运行时间。也就是说，完成一行归并所需的运行时间取决于这一行的数据量。

看一下这个图便能得知，无论哪一行都是 n 个数据，所以每行的运行时间都为 O(n)。

归并排序每一行的数据都是 n 个

而将长度为 n 的序列对半分割直到只有一个数据为止时，可以分成 行，因此，总共有 log2n 行。也就是说，总的运行时间为 ，这与前面讲到的快速排序相同。