C语言 单向环形链表
三分苦 人气:0目录
1、例题引入
链接直达:
题目:
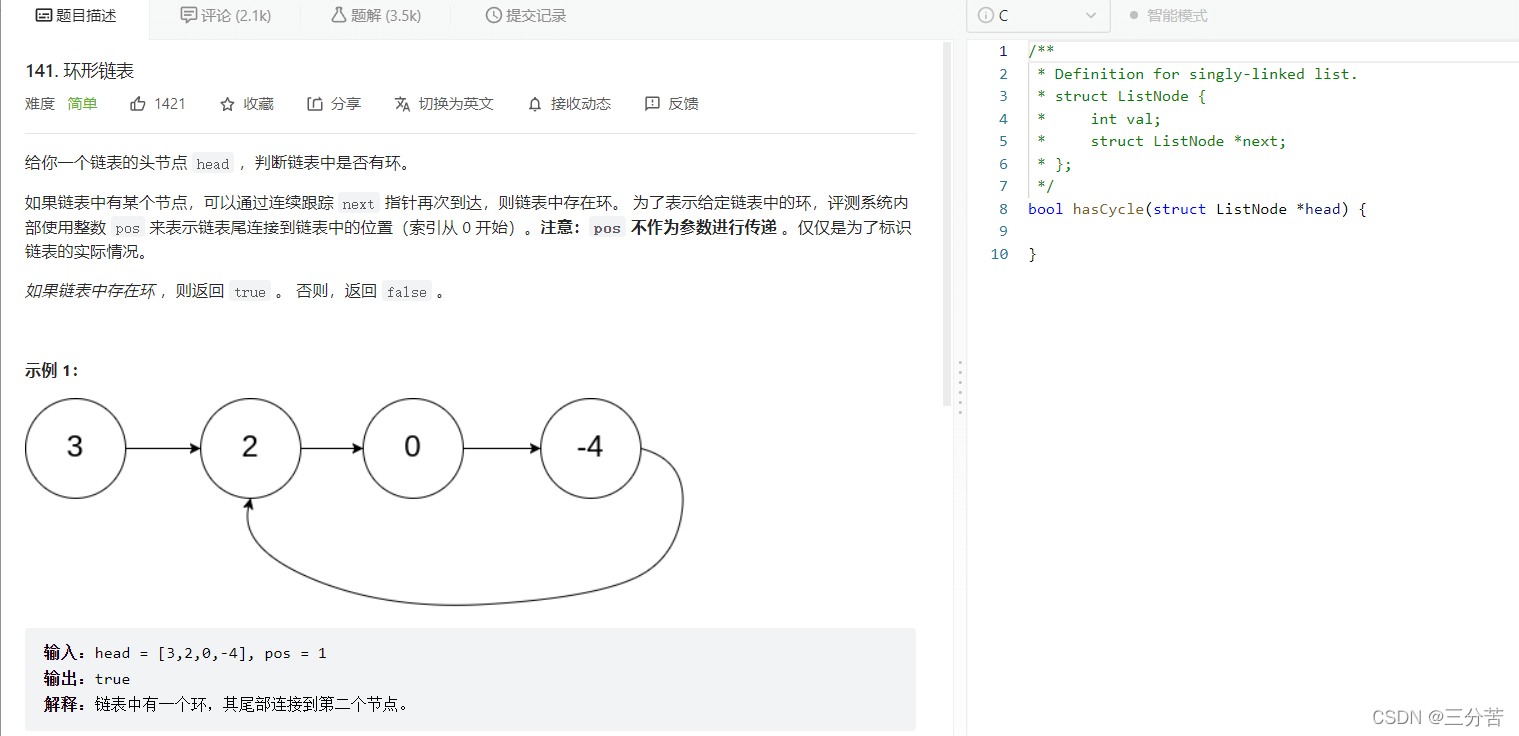
2、何为带环链表
正常的单链表每个节点顺次链接,最后一个节点指向NULL,如下:

而带环链表的最后一个节点不再指向NULL了,指向的是前面任意一个节点,以此形成带环链表,并一直循环下去。如下:

3、题解思路
我们可以将上述图画的抽象一点,在没有进入环之前我们用直线表示,进入环之后用圈来表示,以此示意循环。此题需要用到我们之前讲解的求中间节点和求倒数第k个节点的快慢指针的思想。定义两个指针slow和fast均指向一开始的位置。 让slow一次走一步,fast一次走两步。
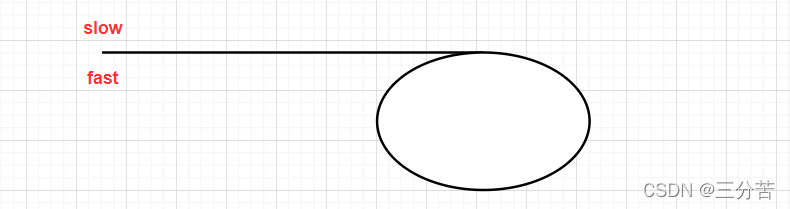
当slow走到直线一半的位置时,此时的fast刚好就在环的入口点。

假设slow刚好走到环的入口点时,fast走到如下位置,此时fast开始追赶模式

fast开始追赶slow,假设fast在如下的位置开始追上slow
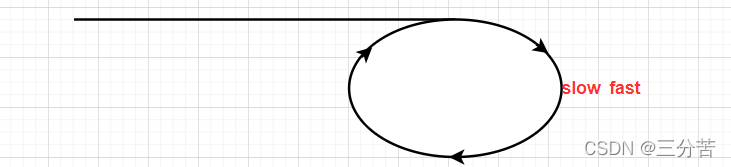
代码如下:
bool hasCycle(struct ListNode *head) {
struct ListNode*slow=head;
struct ListNode*fast=head;
while(fast&&fast->next)
{
slow=slow->next;
fast=fast->next->next;
if(slow==fast)
{
return true;
}
}
return false;
}单纯从解体的角度看,此题并不复杂,仅需用到快慢指针的思想即可解决,单是由此题可以引出多个值得我们探讨的问题,以此来加深我们对环形链表的认知,如下三大拓展问题:
4、拓展问题
- (1)slow一次走1步,fast一次走2步,一定能追上吗?
答案:一定能。
证明:
当slow走到中间的时候,fast一定进环了,此时fast开始追击。我们假设slow进环以后,slow和fast的距离是N,此时slow走1步,fast走2步,它们俩的距离缩短1变为N-1。以此类推,每次追击,距离缩小1,当距离缩小为0时就追上了。综上,一定能追上。

- (2)slow一次走1步,fast一次走3步,能追上吗?fast一次走4步呢?n步呢?
答案:不一定
证明:
我们先来讨论slow一次走1步,fast一次走3步的情况。假设slow走了1步,fast走3步时刚好进环,而当slow刚好进环的时候,fast可能已经走了1圈,具体情况得看环的大小,此时slow和fast之间的距离为N。并假设环的长度是C。
slow一次走1步,fast一次走3步,距离变为N-2。由此可见,fast和slow每走一次,距离缩短2。此时就不难发现了,需要分类讨论,当N是偶数时,刚好可以追上,当N是奇数时,追到最后距离为-1,此时就要再追了,意味着slow和fast之间的距离变成C-1。
继续追击,根据前面的分析,如果C-1是偶数,那么可以追上。如果C-1是奇数,那么就永远追不上了,将会无线循环追下去,可就是追不上。他们的差距N是由进环前的长度和环的长度决定的,而这两个又都是随机的,所以N的值不确定,可奇可偶,又像刚刚那样讨论下去,出现奇数将一去不复返。

同理fast一次走4步也是这样的讨论,同样都是不一定,不过这个时候是每走一次,距离缩短3。当N是3的倍数就可以追上,当不是3的倍数就要继续讨论了,有兴趣的童鞋可以继续钻研下去,思想和fast一次走3步一样,这里不过多赘述。
- (3)链表环的入口点在哪呢?
当我们搞清楚slow和fast分别走的距离时,入口点自然就明了了。
法一:

slow一次走1步,fast一次走2步,那么fast走的距离是slow的2倍
在具体讲解之前,首先要搞清楚,不存在说慢指针slow在里头走了一圈,快指针fast还没有追到slow,因为fast每次走2步,slow每次走1步,它俩间的距离每次都缩小1,所以只会越来越近,直到追到。最多最多也就快1圈,但从来也不会刚好满1圈。所以下面很容易推出slow和fast分别走了多少。
假设:
【链表头 - - - 入口点】:L
【入口点 - - - 相遇点】:X
【环的长度】:C
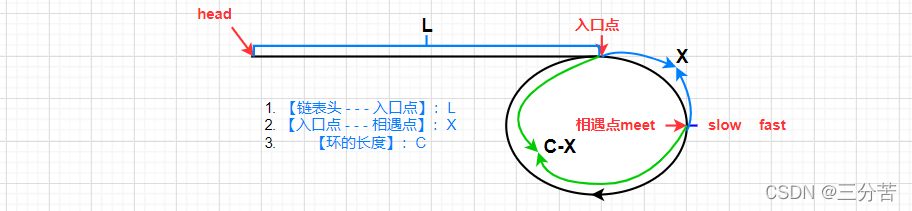
slow走的距离:L + X
fast走的距离:L + N*C + X
解释:
因为先前已经提到slow不会都走了一圈还没被追到,所以很容易推出slow的距离就是L+X
而快指针一次走2步,很可能会因为环过小导致在slow指针进入入口点前,fast指针已经走了好几圈。简而言之3句话:
- L很小,C很大,slow进环前,fast可能在环里面,一圈都没走完
- L很大,C很小,slow进环前,fast在里面走了很多圈了
- 但是slow进环以后,在一圈之内,fast一定追到slow,它们的距离最多C-1
根据一开始说的,fast走的距离是slow走的距离的2倍,可列出如下式子:
2*(L+X) = L + N*C + X
化简后:L+X = N*C 或 L = N*C - X 或 L = (N-1)*C + (C-X) 或 L + X = N*C
用此公式即可证明:一个指针从meet走,一个指针从head走,他们会在入口点相遇!
因为式子(N-1)*C表明从相遇点走了N-1圈后又回到了相遇点,此时再走C-X的距离就回到了入口点,由上得知,此公式确实让它们回到了入口点。
用一道切实的题目来具体解出入口点的位置:
链接直达:
题目:
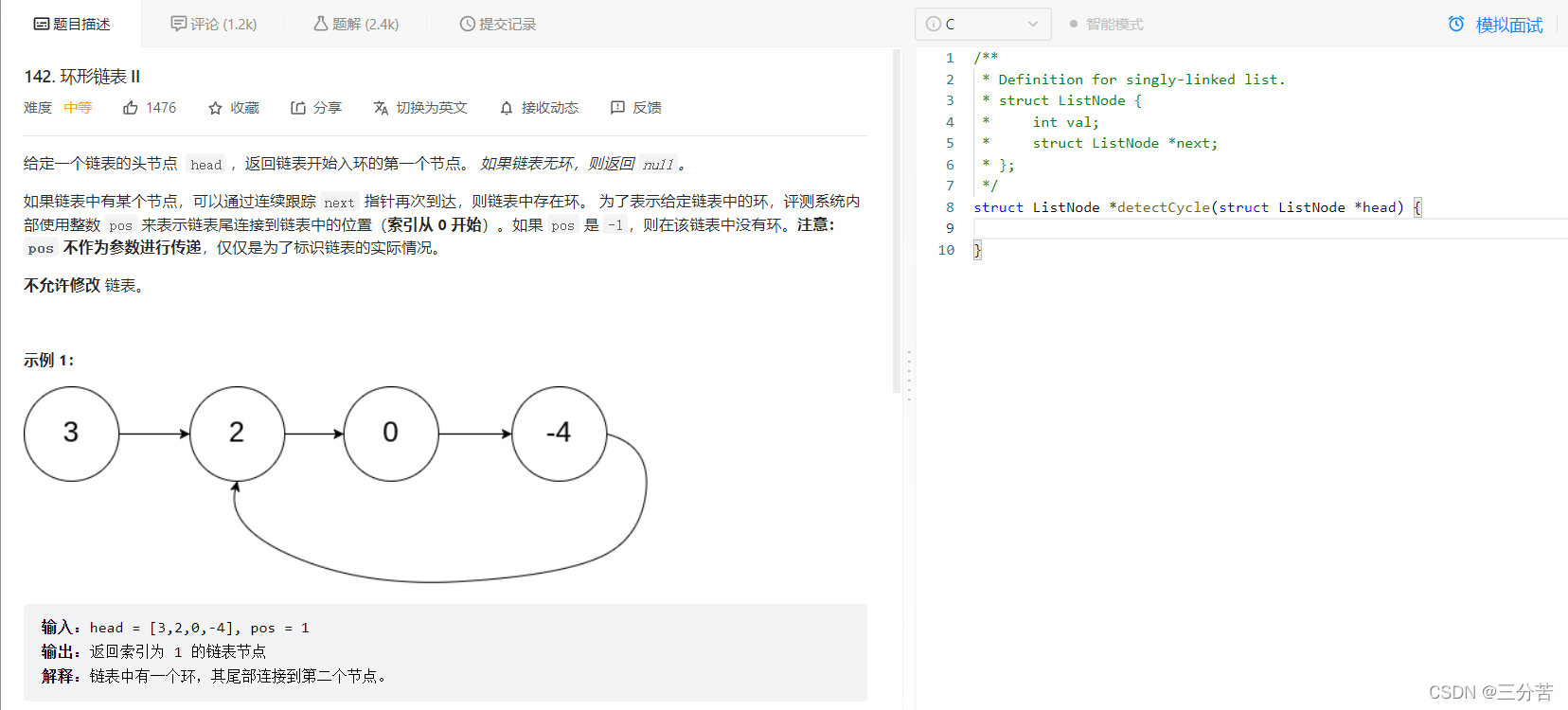
代码如下:
struct ListNode* detectCycle(struct ListNode* head) {
struct ListNode* slow = head;
struct ListNode* fast = head;
while (fast && fast->next)
{
//判断是否是带环链表
slow = slow->next;
fast = fast->next->next;
if (slow == fast)
{
struct ListNode* meet = slow;
while (meet != head)
{
//求出相遇点
meet = meet->next;
head = head->next;
}
return meet;
}
}
return NULL;
}求相遇点还有另外一种方法:
找到相遇点meet后,让meet做尾,让下一个点做新链表的头

此法显的尤为巧妙,刚好转换成了两个链表求交点的问题。因为此时headA链表的尾部是meet,而headB链表的尾部也是meet,此时就意味着俩链表必会相交,而相交的地方就是入口点,两链表相交正是博主上篇博文中所详细讲解的,这里就不过多强调了。
加载全部内容