图论数据结构霍夫曼树及其编码
威斯布鲁克.猩猩 人气:0霍夫曼树
一、基本介绍

二、霍夫曼树几个重要概念和举例说明
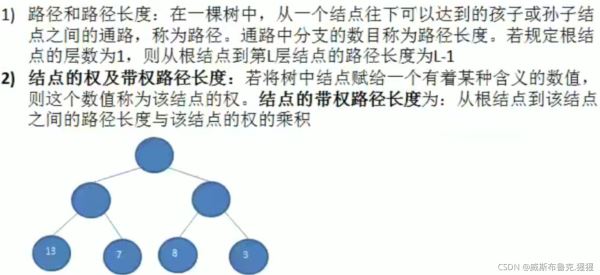

构成霍夫曼树的步骤

举例:以arr = {1 3 6 7 8 13 29}
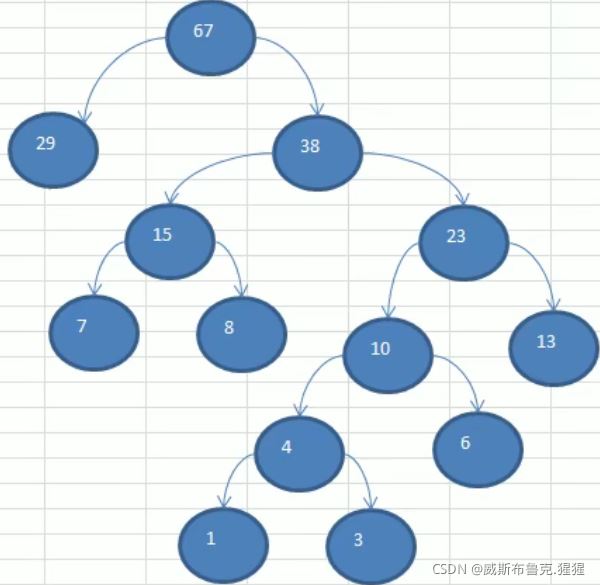
public class HuffmanTree {
public static void main(String[] args) {
int[] arr = { 13, 7, 8, 3, 29, 6, 1 };
Node root = createHuffmanTree(arr);
preOrder(root);
}
// 编写一个前序遍历的方法
public static void preOrder(Node root) {
if (root != null) {
root.preOrder();
} else {
System.out.println("树是空树,无法遍历~~");
}
}
// 创建赫夫曼树的方法
/**
* @param arr 需要创建成霍夫曼树的数组
* @return 创建好后的霍夫曼树的root节点
*/
public static Node createHuffmanTree(int[] arr) {
// 第一步为了操作方便
// 1.遍历 arr 数组
// 2.将 arr 的每个元素构成一个Node
// 3.将Node 放入到ArrayList中
List<Node> nodes = new ArrayList<Node>();
for (int value : arr) {
nodes.add(new Node(value));
}
while (nodes.size() > 1) {
// 排序从小到大
Collections.sort(nodes);
System.out.println("nodes = " + nodes);
// 取出根节点权值最小的两颗二叉树
//注意:如果是从大到小排列的:就应该取倒数第一个和倒数第二个
// (1) 取出权值最小的节点(二叉树)
Node leftNode = nodes.get(0);
// (2) 取出权值第二小的节点(二叉树)
Node rightNode = nodes.get(1);
// (3) 构建一颗新的二叉树
Node parent = new Node(leftNode.value + rightNode.value);
parent.left = leftNode;
parent.right = rightNode;
// (4) 从ArrayList删除处理过的二叉树
nodes.remove(leftNode);
nodes.remove(rightNode);
// (5) 将parent加入到nodes
nodes.add(parent);
}
// 返回赫夫曼树的root节点
return nodes.get(0);
}
}
//创建节点类
//为了让Node对象支持排序Collections集合排序
//让Node实现Comparable接口
class Node implements Comparable<Node> {
int value;// 节点权值
Node left;// 指向左子节点
Node right;// 指向右子节点
public Node(int value) {
this.value = value;
}
// 写一个前序遍历
public void preOrder() {
System.out.println(this);
if (this.left != null) {
this.left.preOrder();
}
if (this.right != null) {
this.right.preOrder();
}
}
@Override
public String toString() {
return "Node [value=" + value + "]";
}
@Override
public int compareTo(Node o) {
// 表示从小到大排列
return this.value - o.value;
}
}
霍夫曼编码
一、基本介绍

二、原理剖析





6)说明:
原来长度是359,压缩了(359 - 133) / 359 = 62.9%
此编码满足前缀编码,即字符的编码都不能是其他字符编码的前缀。不会造成匹配的多义性;
霍夫曼编码是无损的压缩处理方案
注意:




霍夫曼编码压缩文件注意事项
1)如果文件本身就是经过压缩处理的,那么使用赫夫曼编码在压缩效率不会有明显变化,比如视频,ppt等等文件
2)赫夫曼编码是按字节来处理的,因此可以处理所有的文件(二进制文件、文本文件)
3)如果一个文件中的内容,重复的数据不多,压缩效果也不会很明显。
加载全部内容