python梯度下降
这里是阿丁 人气:0简单批量梯度下降代码
其中涉及到公式
alpha表示超参数,由外部设定。过大则会出现震荡现象,过小则会出现学习速度变慢情况,因此alpha应该不断的调整改进。


注意1/m前正负号的改变
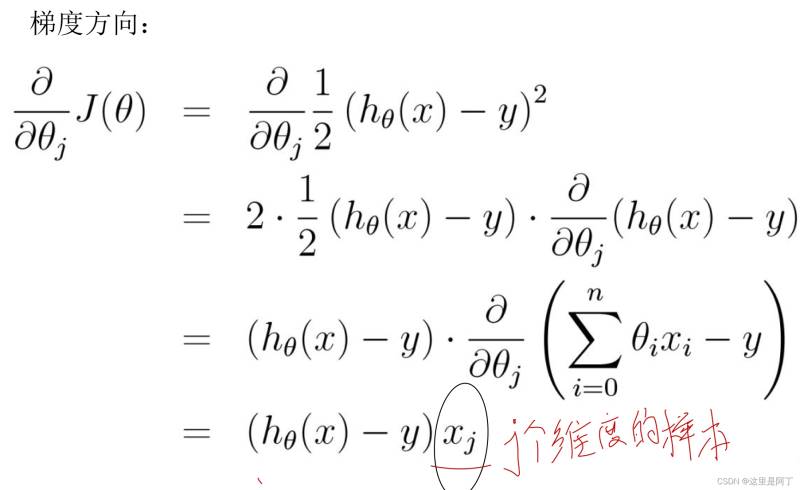
Xj的意义为j个维度的样本。
下面为代码部分
import numpy as np
#该处数据和linear_model中数据相同
x = np.array([4,8,5,10,12])
y = np.array([20,50,30,70,60])
#一元线性回归 即 h_theta(x)= y= theta0 +theta1*x
#初始化系数,最开始要先初始化theta0 和theta1
theta0,theta1 = 0,0
#最开始梯度下降法中也有alpha 为超参数,提前初始化为0.01
alpha = 0.01
#样本的个数 ,在梯度下降公式中有x
m = len(x)
#设置停止条件,即梯度下降到满足实验要求时即可停止。
# 方案1:设置迭代次数,如迭代5000次后停止。
#(此处为2)方案2:设置epsilon,计算mse(均方误差,线性回归指标之一)的误差,如果mse的误差《= epsilon,即停止
#在更改epsilon的次数后,越小,迭代次数会越多,结果更加准确。
epsilon = 0.00000001
#设置误差
error0,error1 = 0,0
#计算迭代次数
cnt = 0
def h_theta_x(x):
return theta0+theta1*x
#接下来开始各种迭代
#"""用while 迭代"""
while True:
cnt+=1
diff=[0,0]
#该处为梯度,设置了两个梯度后再进行迭代,梯度每次都会清零后再进行迭代
for i in range(m):
diff[0]+=(y[i]-h_theta_x(x[i]))*1
diff[1]+=(y[i]-h_theta_x(x[i]))*x[i]
theta0 = theta0 + alpha * diff[0] / m
theta1 = theta1 + alpha * diff[1] / m
#输出theta值
# ”%s“表示输出的是输出字符串。格式化
print("theta0:%s,theta1:%s"%(theta0,theta1))
#计算mse
for i in range(m):
error1 +=(y[i]-h_theta_x(x[i]))**2
error1/=m
if(abs(error1-error0)<=epsilon):
break
else:
error0 = error1
print("迭代次数:%s"%cnt)
#线性回归结果:5.714285714285713 1.4285714285714448 87.14285714285714
#批量梯度下降结果:theta0:1.4236238440026219,theta1:5.71483960227916 迭代次数:3988
#在更改epsilon的次数后,越小,迭代次数会越多,结果更加准确。
在线性模型的代码(代码可参见另一条文章)中,得到运算结果a,b的值,与梯度下降后得到的结果theta0和theta1相近。增加实验次数(如修改epsilon的次数)可以得到更为相近的结果。
运行完毕后发现其实该处理方式并不理想
因为梯度下降开始后,theta数量会增加,即变量也会增加。每次增加都需要重新编写其中的循环和函数。
因此可以将他们编写成向量的形式
import numpy as np
#X_b = np.array([[1,4],[1,8],[1,5],[1,10],[1,12]])
#y = np.array([20,50,30,70,60])
#改写成向量形式
#运用random随机生成100个样本
np.random.seed(1)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.rand(100, 1)
X_b = np.c_[np.ones((100, 1)), X]
#print(X_b)
#此处的learning_rate 就是alpha
learning_rate = 0.01
#设置最大迭代次数,避免学习时间过长
n_iterations = 10000
#样本格数
m = 100
#初始化thata, w0...wn,初始化两个2*1 的随机数
theta = np.random.randn(2, 1)
#不会设置阈值,直接设置超参数,迭代次数,迭代次数到了,我们就认为收敛了。先看结果,如果结果不好就去调参
for _ in range(n_iterations):
#接着求梯度gradient,这儿的梯度是n个梯度。即x* (h_theta - y)
#会得到一次迭代的n个theta值
gradients = 1/m * X_b.T.dot(X_b.dot(theta)-y)
#应用公式调整theta的值,theta_t + 1 = theta_t - grad * learning_rate , 是一个向量
theta = theta - learning_rate * gradients
print(theta)
加载全部内容