C语言时间复杂度

一、时间复杂度

1.什么是时间复杂度？

空间效率，时间效率（较为关注）

时间复杂度：算法中的操作执行次数，为算法的时间复杂度。（不是具体时间，而是执行次数）

2.如何计算？

时间复杂度

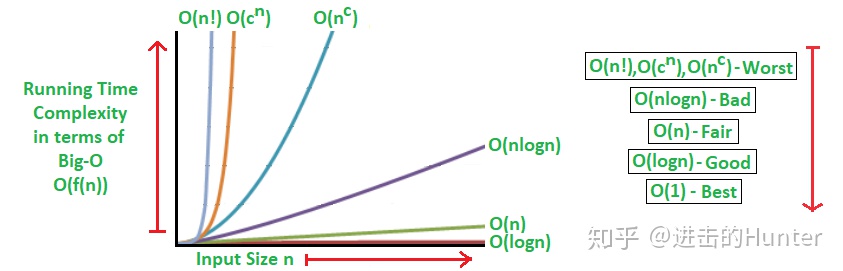
（1）是一个估算，看表达式中影响大的那一项，如N*N+2N+10中，N*N对整个式子影响最大，故其时间复杂度为N*N，用大O的渐近表示法O（N*N）。

（2）去掉时间表达式中的常数项乘积，例如，得到一个准确的时间表达式为2N+10，则估算得到的时间复杂度为O（N）

（3）对于多个未知数时，例如时间表达式为N+M，假设M，N差不多大，则O（M）或O（N）；假设M远大于N，则O（M）。

（4）用常数1去替代所有确定的常数，如准确的时间表达式为100，O（1）.

（5）未知数和常数，滤去常数。

（6）另外有些算法分为最好，最坏，平均这三种情况。当算法存在这三种情况时，选最坏的时间复杂度，例如假设字符串长度为N，“sdsfrsgtr...”,遍历字符串，求S的时间复杂度，最好O（1），最坏O（N），平均O（N/2）。

A.  在冒泡排序中，

     第一趟冒泡：N

     第二趟冒泡：N-1

     第三趟冒泡：N-2

     第N趟冒泡：1

     为等差数列，准确次数为：        N*(N+1)/2

故冒泡排序时间复杂度为O（N*N）

B.  在二分查找/折半查找中：

假设二分了X次，有1*2*2....*2=N，2^X=N, X=(log2) N

算法的复杂度计算中，喜欢省略成logN，因为不好写底数，但是写成lg N,是错的。

C.  在某些阶乘的运算中求时间复杂度：

long long Factorial(size_t N)
{
   return N<2 ? N:Factorial(N-1)*N;
}

如Factorial(10),则返回factorial（9）*10,在返回到factorial（9）*8.....以此类推返回到

factorial（1）*2返回到1.（实际是10！）递归了N次，故时间复杂度为O（N）。（特别注意：结返回结果是N！，但是操作的次数是递归了N次，所以时间复杂度为O（N））

3.常见的时间复杂度：

 二、空间复杂度

1.什么是空间复杂度？

空间复杂度是算法运行过程中临时占用存储空间大小的量度，不在意其具体占了多少比特的大小，而是计算变量的个数。

2.如何计算？

对照时间复杂度的计算方法。注意：时间是累积的，空间是不累计的，空间可以销毁。

例题1：消失的数字

思路1：排序 0 1 2 3 4 5 6 7 9 一次比较，若下一个数与上一个数只差为1，则掠过，若下一个数比上一个数>1，则找到，但时间复杂度不符合。

思路2：把0到N加到一起，结果ret1,再把数组中的数加到一起ret2，ret1-ret2就是要找的数。

思路3：异或：相同为0，相异为1。将数组中的数与0-N数互相异或，最后剩下的那个数字就是缺的那个数。

int missingNumber(int* nums, int numsSize){
    int x=0;
    //先和数组的数进行异或
    for(int i=0;i<numsSize;++i)
    {
        x^=nums[i];
    }
    //在和0-N的数进行异或
    for(int j=0;j<numsSize+1;++j)
    {
        x^=j;
    }
return x;
}

要注意0-N数异或时，注意j<numsSize+1，它比原数组中元素个数多1。

 例题2：旋转数组

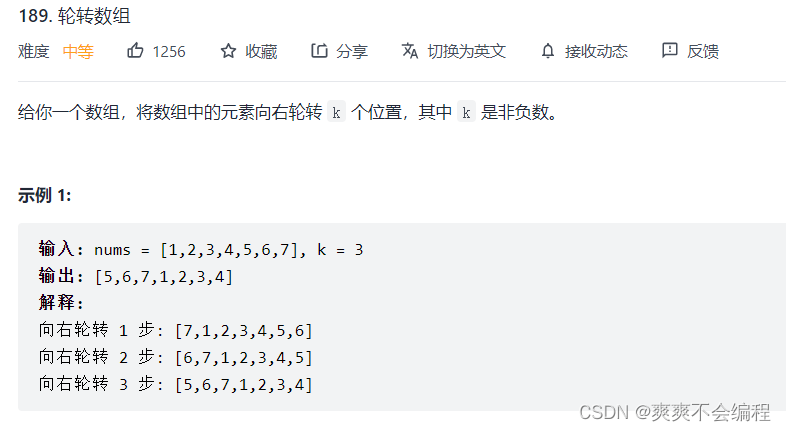
思路1：保存最后一个数，将其挪到前面来。k次

void rotate(int* nums, int numsSize, int k){
    for(int i=0;i<k;++i)
    {
    int tmp=nums[numsSize -1];
    for(int end=numsSize -2;end >=0;--end)
    {
        nums[end+1]=nums[end];
    }
    nums[0]=tmp;
    }
}

但此时时间复杂度为O（N*K），跑不过~

思路2：以空间换时间，尝试着多消耗一点空间，一次换成。将后K个保存，移到前面来，直接得到。时间复杂度为O（N），空间复杂度为O（N）

思路3：后K个逆置，前K个逆置，整体逆置（这个实在是太牛了！！）

 c代码为：

//逆置
void Reverse(int *nums ,int left,int right){
    while(left<right)
    {
        int tmp=nums[left];
        nums[left]=nums[right];
        nums[right]=tmp;
        ++left;
        --right;
    }
}
void rotate(int* nums, int numsSize, int k)
{
    //控制好下标,后N-K个
    Reverse(nums,numsSize-k,numsSize-1);
    Reverse(nums,0,numsSize-k-1);
    Reverse(nums,0,numsSize-1);
 
}

 注意结果可能出错：

 此时需要注意K是否大于N，当K>N时需要取模：k%=numsSize

添加：if（K>numsSize）{ K%numsSize;}

//逆置
void Reverse(int *nums ,int left,int right){
    while(left<right)
    {
        int tmp=nums[left];
        nums[left]=nums[right];
        nums[right]=tmp;
        ++left;
        --right;
    }
}
void rotate(int* nums, int numsSize, int k)
{
    if(k>numsSize)
    {
        k%=numsSize;
    }
    //控制好下标,后N-K个
    Reverse(nums,numsSize-k,numsSize-1);
    Reverse(nums,0,numsSize-k-1);
    Reverse(nums,0,numsSize-1);
 
}

在力扣上运行得到：

总结