C语言二叉树

时间:2022-05-23 不吃香菜的香菜头子人气:0

在本算法中先利用先序遍历创建了树，利用了递归的算法使得算法简单，操作容易，本来无printf("%c的左/右子树：", ch);的语句，但由于计算机需要输入空格字符来判断左右子树，为了减少人为输入的失误，特地加入这条语句，以此保证准确率。

#include<stdio.h>
#include<stdlib.h>
#define OK 1
#define ERROR 0
#define OVERFLOW 3
 
typedef int Status;  
typedef int Boolean; 
typedef char TElemType;
 
typedef struct BiTNode{
	TElemType	   data;
	struct BiTNode *lchild, *rchild;
}BiTNode, *BiTree;
 
//创建二叉树函数
 
Status CreateBiTree(BiTree &T){
	TElemType ch;
	scanf("%c", &ch);
	getchar();
	if(ch == ' '){	T = NULL;}
	else {
		if( !(T=(BiTree)malloc(sizeof(BiTNode))))(exit(OVERFLOW));
		T->data = ch;				
		printf("%c的左子树：", ch);
		CreateBiTree(T->lchild);		
		printf("%c的右子树：", ch);
		CreateBiTree(T->rchild);	}
	return OK;
}
 
//先序遍历函数
Status PreOrderTraverse(BiTree T, Status (* Visit)(TElemType e)){
	if(T){
		if(Visit(T->data)){
			if(PreOrderTraverse(T->lchild, Visit)){
				if(PreOrderTraverse(T->rchild, Visit)){
					return OK;
               }	
            }	
         }
		return ERROR;
    }
	else {return OK;}
}
 
//中序遍历函数
Status InOrderTraverse(BiTree T, Status (* Visit)(TElemType e)){
	if(T){
		if(PreOrderTraverse(T->lchild, Visit) ){
			if(Visit(T->data)){
				if(PreOrderTraverse(T->rchild, Visit) ){
					return OK;
           }
	   }	
   }
		return ERROR;
        }
	else {
		return OK;
        }
	}
 
//后序遍历函数
Status PosOrderTraverse(BiTree T, Status (* Visit)(TElemType e)){
	if(T){
		if(PreOrderTraverse(T->lchild, Visit) ){
			if(PreOrderTraverse(T->rchild, Visit) ){
				if(Visit(T->data)){return OK;
}
	}	
}
		return ERROR;}
	else {return OK;
}
}
 
 
//输出二叉树函数
Status PrintElement(TElemType e){	
	printf("%c",e);
	return OK;
}
 
//主函数
int main(){
	BiTree T;
	printf("输入根结点：");
	CreateBiTree(T);
	printf("先序遍历：\n");
	PreOrderTraverse(T, PrintElement);
	printf("\n");
	printf("中序遍历：\n");
	InOrderTraverse(T, PrintElement);
	printf("\n");
	printf("后序遍历：\n");
	PosOrderTraverse(T, PrintElement);
	return 0;
}

遍历操作有四种，其不同在于对根结点的访问顺序不同。在先序遍历中，首先访问根结点，然后递归地做左子树的先序遍历，然后是右子树的递归先序遍历。在中序遍历中，递归地对左子树进行中序遍历，访问根结点，最后递归中序遍历右子树。在后序遍历中，递归地对左子树和右子树进行后序遍历，然后访问根结点。先序，中序，后序遍历就是对于根节点的访问顺序。

但无论哪种遍历方式，递归的方法是最简便，最直接，最简单的算法。

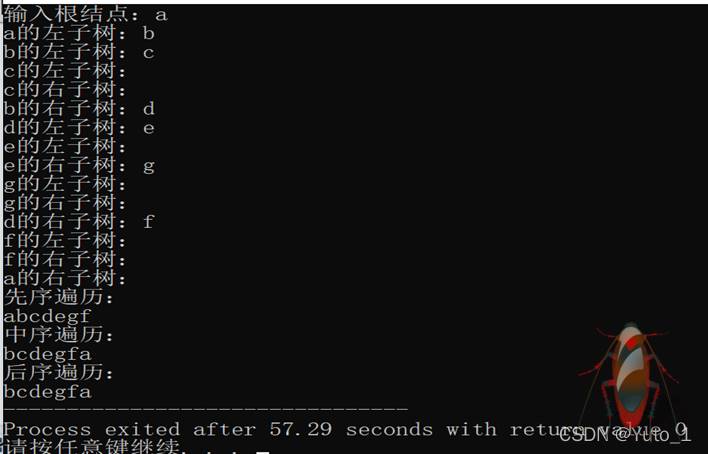
运行截图：

加载全部内容