Java链表数据结构

时间:2022-05-23 胡安民人气:0

什么是链表？

链表是一种物理存储单元上非连续、非顺序的存储结构，数据元素的逻辑顺序是通过链表中的指针连接次序实现的。
每一个链表都包含多个节点，节点又包含两个部分，一个是数据域（储存节点含有的信息），一个是引用域（储存下一个节点或者上一个节点的地址）。

链表的理解示意图:

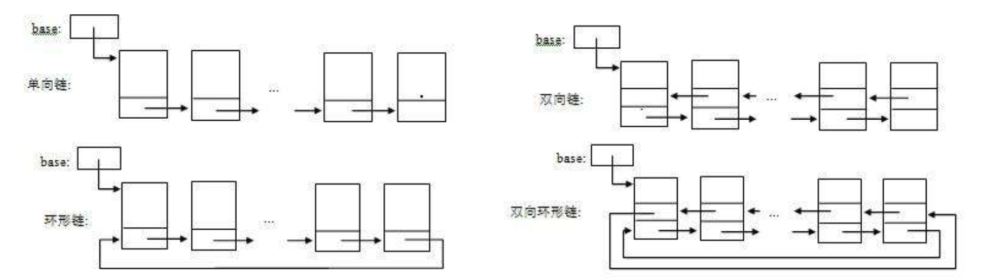
在这里插入图片描述

链表的特点是什么？

获取数据麻烦，需要遍历查找，比数组慢
方便插入、删除

简单的链表的实现原理

创建一个节点类，其中节点类包含两个部分，第一个是数据域（你到时候要往节点里面储存的信息），第二个是引用域（相当于指针，单向链表有一个指针，指向下一个节点；双向链表有两个指针，分别指向下一个和上一个节点）

创建一个链表类，其中链表类包含三个属性：头结点、尾节点和大小，方法包含添加、删除、插入等等方法。通用节点抽象类

package com.lineardatastructure.linked;
/**
 * @author huanmin
 * @param <T>
 */
/**
 * 自定义链表接口定义
 **/
public abstract class LinkedAbs<T> implements Iterable<T> {
    //列表长度
    public int size = 0;
    //当前节点
    public Node head;
    //尾节点
    public Node end;
    //节点
    protected class Node {
        Node previous = null;//上一个结点
        Node next = null;//下一个结点
        T data;//结点数据
        public Node(T data, Node next) {
            this.data = data;
            this.next = next;
        }
        public Node(Node next, Node previous) {
            this.next = next;
            this.previous = previous;
        }
        public Node(T data, Node next, Node previous) {
            this.next = next;
            this.previous = previous;
        }
        public Node(T data) {
            this.data = data;
        }
    }
    /**
     * 判断链表是否有环：
     * 有环返回环的入口节点,没有返回null
     * 设置快指针和慢指针，慢指针每次走一步，快指针每次走两步
     * 当快指针与慢指针相等时，就说明该链表有环,并且这个节点就是环的入口
     */
    public Node isRinged(){
        if(head == null){
            return null;
        }
          Node slow = head;
        Node fast = head;
        while(fast.next != null && fast.next.next != null){
            slow = slow.next;
            fast = fast.next.next;
            if(fast == slow){
                return fast;
            }
        }
        return null;
    }
    // 获取链表头元素
    public T getFrom() {
        return head.data;
    }
    //获取链表结尾元素
    public T getEnd() {
        return end.data;
    }
    //获取链表中元素个数
    public int getSize() {
        return size;
    }
    /**
     * 判断链表中是否为空
     *
     * @return
     */
    public boolean isEmpty() {
        return size == 0;
    }
    /**
     * 销毁链表
     */
    public void stackDestroy() {
        head = null;
        size = 0;
        end=null;
    }
    //寻找单链表的中间结点：
    public  abstract T findMiddle();
    /**
     * 元素反转
     */
    public abstract void reserveLink();
    /**
     * 获取指定元素
     *
     * @param index
     */
    public abstract T get(int index);
    /**
     * 向链表中添加元素
     *
     * @param e
     */
    public abstract void addFirst(T e);
    public abstract void addlast(T e);
    public abstract void add(T e);
    /**
     * 从链表中删除元素
     */
    public abstract boolean remove(T obj);
    public abstract boolean remove(int index);
    public abstract boolean removeFirst();
    public abstract boolean removeLast();
}

实现单向链表

在这里插入图片描述

package com.lineardatastructure.linked;
import java.util.Iterator;
/**
 * @author huanmin
 * @param <T>
 */
// 单向链表
public class OneWayLinked<T> extends LinkedAbs<T> {
    @Override
    public void reserveLink() {
        Node curNode = head;//头结点
        Node preNode = null;//前一个结点
        while(curNode != null){
            Node nextNode = curNode.next;//保留下一个结点
            curNode.next = preNode;//指针反转
            preNode = curNode;//前结点后移
            curNode = nextNode;//当前结点后移
        }
        head = preNode;
    }
    /**
     * 寻找单链表的中间结点：
     * 方法一、先求出链表的长度，再遍历1/2链表长度，寻找出链表的中间结点
     * 方法二、：
     * 用两个指针遍历链表，一个快指针、一个慢指针，
     * 快指针每次向前移动2个结点，慢指针一次向前移动一个结点，
     * 当快指针移动到链表的末尾，慢指针所在的位置即为中间结点所在的位置
     */
    @Override
    public T findMiddle() {
        Node slowPoint = head;
        Node quickPoint = head;
        //quickPoint.next == null是链表结点个数为奇数时，快指针已经走到最后了
        //quickPoint.next.next == null是链表结点数为偶数时，快指针已经走到倒数第二个结点了
        //链表结点个数为奇数时,返回的是中间结点；链表结点个数为偶数时，返回的是中间两个结点中的前一个
        while (quickPoint.next != null && quickPoint.next.next != null) {
            slowPoint = slowPoint.next;
            quickPoint = quickPoint.next.next;
        }
        return slowPoint.data;
    }
    /**
     * 查询指定下标数据
     * @param index
     * @return
     */
    @Override
    public T get(int index) {
        if(size<0 || index>size){//待查询结点不存在
            return null;
        }
        if(index == 0){//查询头结点
            return head.data;
        }
        Node curNode =head;
        int i = 0;
        while (curNode != null) {
            if(i==index){//寻找到待查询结点
                return  curNode.data;
            }
            //当先结点和前结点同时向后移
            curNode = curNode.next;
            i++;
        }
        return null;
    }
    @Override
    public void addFirst(T e) {
    }
    @Override
    public void addlast(T e) {
    }
    /**
     * 链表添加结点:
     * 找到链表的末尾结点，把新添加的数据作为末尾结点的后续结点
     *
     * @param data
     */
    @Override
    public void add(T data) {
        Node newNode = new Node(data);
        if (head == null) {
            head = newNode;
            end=head;//添加尾节点
            size++;
            return;
        }
        Node temp = end;
        temp.next = newNode;
        end=newNode;//修改尾节点
        size++;
    }
    /**
     * 链表删除结点:
     * 把要删除结点的前结点指向要删除结点的后结点，即直接跳过待删除结点
     * @param obj
     * @return
     */
    @Override
    public boolean remove(T obj) {
        if (head.data.equals(obj)) {//删除头结点
            head = head.next;
            size=0;
            return true;
        }
        Node preNode = head;
        Node curNode = preNode.next;
        while (curNode != null) {
            if (curNode.data.equals(obj)) {//寻找到待删除结点
                preNode.next = curNode.next;//待删除结点的前结点指向待删除结点的后结点
                size--;
                return true;
            }
            //当先结点和前结点同时向后移
            preNode = preNode.next;
            curNode = curNode.next;
        }
        return  false;
    }
    @Override
    public boolean remove(int index) {
        if(size<0 || index>size){//待删除结点不存在
            return false;
        }
        if(index == 0){//删除头结点
            head = head.next;
            return true;
        }
        Node preNode = head;
        Node curNode =head.next;
        int i =1; //从第2个值开始
        while(preNode.next != null){
            if(i==index){//寻找到待删除结点
                preNode.next= curNode.next;//待删除结点的前结点指向待删除结点的后结点
                return true;
            }
            //当先结点和前结点同时向后移
            preNode=curNode;
            curNode = curNode.next;
            i++;
        }
        return false;
    }
    @Override
    public boolean removeFirst() {
        return false;
    }
    @Override
    public boolean removeLast() {
        return false;
    }
    @Override
    public Iterator<T> iterator() {
        return new Iterator<T>() {
            Node cursor = head;
            T data;
            @Override
            public boolean hasNext() {
                if (cursor != null) {
                    data = cursor.data;
                    cursor = cursor.next;
                    return true;
                }
                return false;
            }
            @Override
            public T next() {
                return data;
            }
            @Override
            public void remove() {
                OneWayLinked.this.remove(data);
            }
        };
    }
}

单向环形链表

它和单链表的区别在于结尾点的指针域不是指向null，而是指向头结点，形成首尾相连的环。这种首尾相连的单链表称为单向循环链表。循环链表可以从任意一个结点出发，访问到链表中的全部结点。

在这里插入图片描述

单向循环链表的查找、删除和修改操作与单链表一致(这里不在赘述，可参考前面的内容)，插入操作和单链表有所不同，单向循环链表需要维持环状结构。判断单链表为空的条件是head.next == null，而判断单向循环链表为空的条件为head.next == head。

package com.lineardatastructure.linked;
import java.util.Iterator;
/**
 * @param <T>
 * @author huanmin
 */
// 单向循环链表
public class OneLoopWayLinked<T> extends LinkedAbs<T> {
    @Override
    public void reserveLink() {
        Object[] ts = new Object[size];
        int i = size - 1;
        for (T t : this) {
            ts[i] = t;
            i--;
        }
        Node node = head;
        node.data = (T) ts[0];
        for (int i1 = 1; i1 < ts.length; i1++) {
            Node node1 = new Node((T) ts[i1]);
            node.next = node1;
            node = node1;
            end= node1;
        }
        //调整位置
        end.next=head;
    }
    /**
     * 寻找单链表的中间结点：
     * 方法一、先求出链表的长度，再遍历1/2链表长度，寻找出链表的中间结点
     * 方法二、：
     * 用两个指针遍历链表，一个快指针、一个慢指针，
     * 快指针每次向前移动2个结点，慢指针一次向前移动一个结点，
     * 当快指针移动到链表的末尾，慢指针所在的位置即为中间结点所在的位置
     */
    @Override
    public T findMiddle() {
        Node slowPoint = head;
        Node quickPoint = head;
        //quickPoint.next == null是链表结点个数为奇数时，快指针已经走到最后了
        //quickPoint.next.next == null是链表结点数为偶数时，快指针已经走到倒数第二个结点了
        //链表结点个数为奇数时,返回的是中间结点；链表结点个数为偶数时，返回的是中间两个结点中的前一个
        while (quickPoint.next != head && quickPoint.next.next != head) {
            slowPoint = slowPoint.next;
            quickPoint = quickPoint.next.next;
        }
        return slowPoint.data;
    }
    /**
     * 查询指定下标数据
     *
     * @param index
     * @return
     */
    @Override
    public T get(int index) {
        if (size < 0 || index > size) {//待查询结点不存在
            return null;
        }
        if (index == 0) {//查询头结点
            return head.data;
        }
        Node curNode = head.next;
        int i = 1;
        while (curNode != head) {
            if (i == index) {//寻找到待查询结点
                return curNode.data;
            }
            //当先结点和前结点同时向后移
            curNode = curNode.next;
            i++;
        }
        return null;
    }
    @Override
    public void addFirst(T e) {
    }
    @Override
    public void addlast(T e) {
    }
    /**
     * 链表添加结点:
     * 找到链表的末尾结点，把新添加的数据作为末尾结点的后续结点
     *
     * @param data
     */
    @Override
    public void add(T data) {
        Node newNode = new Node(data);
        if (head == null) {
            head = newNode;
            head.next = head; //环型
            end = head;//添加尾节点
            size++;
            return;
        }
        Node temp = end;
        //一直遍历到最后
        temp.next = newNode;
        newNode.next = head;//环型
        end = newNode;//修改尾节点
        size++;
    }
    /**
     * 链表删除结点:
     * 把要删除结点的前结点指向要删除结点的后结点，即直接跳过待删除结点
     *
     * @param obj
     * @return
     */
    @Override
    public boolean remove(T obj) {
        if (head.data.equals(obj)) {//删除头结点
            head = head.next;
            end.next=head;//调整环
            size--;
            return true;
        }
        Node preNode = head;
        Node curNode = preNode.next;
        while (curNode != head) {
            if (curNode.data.equals(obj)) {//寻找到待删除结点
                preNode.next = curNode.next;//待删除结点的前结点指向待删除结点的后结点
                size--;
                return true;
            }
            //当先结点和前结点同时向后移
            preNode = preNode.next;
            curNode = curNode.next;
        }
        return false;
    }
    @Override
    public boolean remove(int index) {
        if (size < 0 || index > size) {//待删除结点不存在
            return false;
        }
        if (index == 0) {//删除头结点
            head = head.next;
            end.next=head;//调整环
            size--;
            return true;
        }
        Node preNode = head;
        Node curNode = head.next;
        int i = 1; //从第2个值开始
        while (preNode.next != head) {
            if (i == index) {//寻找到待删除结点
                preNode.next = curNode.next;//待删除结点的前结点指向待删除结点的后结点
                return true;
            }
            //当先结点和前结点同时向后移
            preNode = curNode;
            curNode = curNode.next;
            i++;
        }
        size--;
        return false;
    }
    @Override
    public boolean removeFirst() {
        return false;
    }
    @Override
    public boolean removeLast() {
        return false;
    }
    @Override
    public Iterator<T> iterator() {
        return new Iterator<T>() {
            Node cursor = head;
            T data;
            @Override
            public boolean hasNext() {
                if (cursor != null&&cursor.next != head) {
                    data = cursor.data;
                    cursor = cursor.next;
                    return true;
                }
                if (cursor != null) {
                    data = cursor.data;
                    cursor = null;
                    return true;
                }
                return false;
            }
            @Override
            public T next() {
                return data;
            }
            @Override
            public void remove() {
                OneLoopWayLinked.this.remove(data);
            }
        };
    }
}

实现双向链表

在这里插入图片描述

package com.lineardatastructure.linked;
import java.util.Iterator;
/**
 * @author huanmin
 * @param <T>
 */
public class BothwayLinked<T> extends LinkedAbs<T> {
    /**
     *  查询指定下标数据
     * @param index
     * @return
     */
    @Override
    public T get(int index) {
        if (size < 0 || index > size) {//待查询结点不存在
            return null;
        }
        if (index == 0) {//查询头结点
            return head.data;
        }
        Node curNode = head;
        int i = 0;
        while (curNode != null) {
            if (i == index) {//寻找到待查询结点
                return curNode.data;
            }
            //当先结点和前结点同时向后移
            curNode = curNode.next;
            i++;
        }
        return null;
    }
    @Override
    public void addFirst(T e) {
        Node next = head;
        Node previous = new Node(e);
        previous.next = next;
        next.previous = previous;
        head=previous;
        size++;
    }
    @Override
    public void addlast(T e) {
        Node newNode = new Node(e);
        if (head == null) {
            head = newNode;
            size++;
            end=head;//添加尾节点
            return;
        }
        Node temp = end;
        temp.next = newNode;
        newNode.previous = temp;
        end=newNode;//修改尾节点
        size++;
    }
    @Override
    public void add(T e) {
        addlast(e);
    }
    @Override
    public boolean remove(T obj) {
        if (removeHead()) {
            return true;
        }
        Node curNode = head;
        while (curNode != null) {
            //寻找到待删除结点
            if (curNode.data.equals(obj)) {
                //将删除的节点后节点,覆盖删除的节点,然后将父节点指向被删除元素的父节点
                Node previous = curNode.previous;
                Node next = curNode.next;
                if (next == null) {
                    //删除的是最后节点,那么就把他上一个节点的下一个节点删除
                    previous.next=null;
                } else if (previous==null) {
                    //删除的是头节点的话,那么就不管父节点了
                    head=head.next;
                    head.previous=null;
                } else {
                    next.previous = previous;
                    previous.next = next;
                }
                size--;
                return true;
            }
            //当先结点向后移
            curNode = curNode.next;
        }
        return false;
    }
    @Override
    public boolean remove(int index) {
        if (index<0 ||index >= size) {//待删除结点不存在
            return false;
        }
        if (removeHead()) {
            return true;
        }
        Node curNode = head;
        int i = 0;
        while (curNode != null) {
            if (i == index) {//寻找到待删除结点
                //将删除的节点后节点,覆盖删除的节点,然后将父节点指向被删除元素的父节点
                Node previous = curNode.previous;
                Node next = curNode.next;
                if (next == null) {
                    //删除的是最后节点,那么就把他上一个节点的下一个节点删除
                    previous.next=null;
                } else if (previous==null) {
                    //删除的是头节点的话,那么就不管父节点了
                    head=head.next;
                    head.previous=null;
                } else {
                    next.previous = previous;
                    previous.next = next;
                }
                size--;
                return true;
            }
            //当先结点向后移
            curNode = curNode.next;
            i++;
        }
        return false;
    }
    @Override
    public boolean removeFirst() {
        if (removeHead()) {
            return true;
        }
        Node node = head.next;
        node.previous = null;
        head = node;
        size--;
        return false;
    }
    @Override
    public boolean removeLast() {
        if (removeHead()) {
            return true;
        }
        //删除尾节点
        end.previous.next=null;
        size--;
        return true;
    }
    //如果只有一个元素那么就将头删除
    public boolean removeHead() {
        if (head.next==null) {
            head=null;
            return true ;
        }
        return  false;
    }
    @Override
    public void reserveLink() {
        Object[] ts = new Object[size];
        int i = size - 1;
        for (T t : this) {
            ts[i] = t;
            i--;
        }
        Node node = head;
        node.data = (T) ts[0];
        for (int i1 = 1; i1 < ts.length; i1++) {
            Node node1 = new Node((T) ts[i1]);
            node.next = node1;
            node1.previous = node;
            node = node1;
        }
    }
    /**
     * 寻找单链表的中间结点：
     * 方法一、先求出链表的长度，再遍历1/2链表长度，寻找出链表的中间结点
     * 方法二、：
     * 用两个指针遍历链表，一个快指针、一个慢指针，
     * 快指针每次向前移动2个结点，慢指针一次向前移动一个结点，
     * 当快指针移动到链表的末尾，慢指针所在的位置即为中间结点所在的位置
     */
    @Override
    public T findMiddle() {
        Node slowPoint = head;
        Node quickPoint = head;
        //quickPoint.next == null是链表结点个数为奇数时，快指针已经走到最后了
        //quickPoint.next.next == null是链表结点数为偶数时，快指针已经走到倒数第二个结点了
        //链表结点个数为奇数时,返回的是中间结点；链表结点个数为偶数时，返回的是中间两个结点中的前一个
        while (quickPoint.next != null && quickPoint.next.next != null) {
            slowPoint = slowPoint.next;
            quickPoint = quickPoint.next.next;
        }
        return slowPoint.data;
    }
    @Override
    public Iterator<T> iterator() {
        return new Iterator<T>() {
            Node cursor = head;
            T data;
            @Override
            public boolean hasNext() {
                if (cursor != null) {
                    data = cursor.data;
                    cursor = cursor.next;
                    return true;
                }
                return false;
            }
            @Override
            public T next() {
                return data;
            }
            @Override
            public void remove() {
                BothwayLinked.this.remove(data);
            }
        };
    }
}

双向循环链表

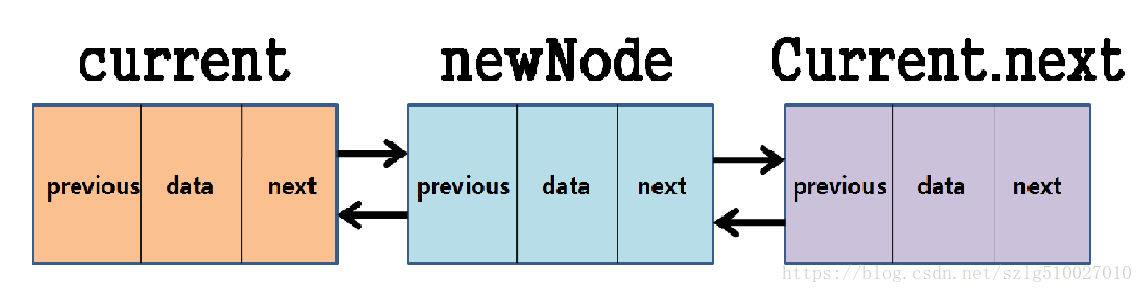
相比单链表，双向循环链表是一个更加复杂的结构。因为双向循环链表的节点不仅包含指向下一个节点的指针(next)，还包含指向前一个节点的指针(prev)。
在双向循环链表中，可见的不只有头指针head，还有尾节点end。这是和单链表的区别。
双向循环链表的头指针head的前一个节点指向end，尾节点end的后一个节点指向head。

在这里插入图片描述

注意: 双向循环链表,实现反查询特别容易只需要反过来遍历一遍就行

package com.lineardatastructure.linked;
import org.w3c.dom.Node;
import java.util.Iterator;
/**
 * @param <T>
 * @author huanmin
 */
public class BothwayLoopLinked<T> extends LinkedAbs<T> {
    @Override
    public void reserveLink() {
        Object[] ts = new Object[size];
        int i = size - 1;
        for (T t : this) {
            ts[i] = t;
            i--;
        }
        Node node = head;
        node.data = (T) ts[0];
        for (int i1 = 1; i1 < ts.length; i1++) {
            Node node1 = new Node((T) ts[i1]);
            node.next = node1;
            node1.previous = node;
            node = node1;
            end= node1;
        }
        //调整位置
        head.previous=end;
        end.next=head;
    }
    /**
     * 寻找单链表的中间结点：
     * 方法一、先求出链表的长度，再遍历1/2链表长度，寻找出链表的中间结点
     * 方法二、：
     * 用两个指针遍历链表，一个快指针、一个慢指针，
     * 快指针每次向前移动2个结点，慢指针一次向前移动一个结点，
     * 当快指针移动到链表的末尾，慢指针所在的位置即为中间结点所在的位置
     */
    @Override
    public T findMiddle() {
        Node slowPoint = head;
        Node quickPoint = head;
        //quickPoint.next == null是链表结点个数为奇数时，快指针已经走到最后了
        //quickPoint.next.next == null是链表结点数为偶数时，快指针已经走到倒数第二个结点了
        //链表结点个数为奇数时,返回的是中间结点；链表结点个数为偶数时，返回的是中间两个结点中的前一个
        while (quickPoint.next != head && quickPoint.next.next != head) {
            slowPoint = slowPoint.next;
            quickPoint = quickPoint.next.next;
        }
        return slowPoint.data;
    }
    /**
     *  查询指定下标数据
     * @param index
     * @return
     */
    @Override
    public T get(int index) {
        if (size < 0 || index > size) {//待查询结点不存在
            return null;
        }
        if (index == 0) {//查询头结点
            return head.data;
        }
        Node curNode = head.next;
        int i = 1;
        while ( curNode!= head) {
            if (i == index) {//寻找到待查询结点
                return curNode.data;
            }
            //当先结点和前结点同时向后移
            curNode = curNode.next;
            i++;
        }
        return null;
    }
    @Override
    public void addFirst(T e) {
        Node next = head;
        Node previous = new Node(e);
        previous.previous = head.previous;
        previous.next = next;
        next.previous = previous;
        head = previous;
        end.next=previous;//修改尾节点的指向
        size++;
    }
    @Override
    public void addlast(T e) {
        Node newNode = new Node(e);
        if (head == null) {
            head = newNode;
            head.previous=head;//环型
            head.next=head; //环型
            end=head;//添加尾节点
            size++;
            return;
        }
        Node temp = end;
        temp.next = newNode;
        newNode.previous = temp;
        newNode.next = head;//给为节点添加头节点(环型)
        end=newNode;//修改尾节点
        size++;
    }
    @Override
    public void add(T e) {
        addlast(e);
    }
    @Override
    public boolean remove(T obj) {
        if (removeHead()) {
            return true;
        }
        //头部删除需要特殊处理
        if (obj == head.data) {
            Node previous = head.previous;
            head = head.next;
            head.previous = previous;
            end.next=head;
            size--;
            return true;
        }
        Node curNode = head.next;
        while (curNode != head) {
            //寻找到待删除结点
            if (curNode.data.equals(obj)) {
                //将删除的节点后节点,覆盖删除的节点,然后将父节点指向被删除元素的父节点
                Node previous = curNode.previous;
                Node next = curNode.next;
                if (next == null) {
                    //删除的是最后节点,那么就把他上一个节点的下一个节点删除
                    previous.next = null;
                } else {
                    next.previous = previous;
                    previous.next = next;
                }
                size--;
                return true;
            }
            //当先结点向后移
            curNode = curNode.next;
        }
        return false;
    }
    @Override
    public boolean remove(int index) {
        if (removeHead()) {
            return true;
        }
        if (size < 0 || index >= size) {//待删除结点不存在
            return false;
        }
        //头部删除需要特殊处理
        if (index==0) {
            Node previous = head.previous;
            head = head.next;
            head.previous = previous;
            size--;
            return true;
        }
        Node curNode = head.next;
        int i = 1;
        while (curNode != null) {
            if (i == index) {//寻找到待删除结点
                //将删除的节点后节点,覆盖删除的节点,然后将父节点指向被删除元素的父节点
                Node previous = curNode.previous;
                Node next = curNode.next;
                if (next == null) {
                    //删除的是最后节点,那么就把他上一个节点的下一个节点给替换成头节点
                    previous.next = head;
                } else {
                    next.previous = previous;
                    previous.next = next;
                }
                size--;
                return true;
            }
            //当先结点向后移
            curNode = curNode.next;
            i++;
        }
        return false;
    }
    @Override
    public boolean removeFirst() {
        head = head.next;
        head.previous = end; //环绕
        end.next=head; //环绕
        size--;
        return false;
    }
    @Override
    public boolean removeLast() {
        //将删除结尾节点
        end.previous.next=head;
        size--;
        return true;
    }
    //如果只有一个元素那么就将头删除
    public boolean removeHead() {
        if (head.next==null) {
            head=null;
            return true ;
        }
        return  false;
    }
    @Override
    public Iterator<T> iterator() {
        return new Iterator<T>() {
            Node cursor = head;
            T data;
            @Override
            public boolean hasNext() {
                if (cursor != null&&cursor.next != head) {
                    data = cursor.data;
                    cursor = cursor.next;
                    return true;
                }
                if (cursor != null) {
                    data = cursor.data;
                    cursor = null;
                    return true;
                }
                return false;
            }
            @Override
            public T next() {
                return data;
            }
            @Override
            public void remove() {
                BothwayLoopLinked.this.remove(data);
            }
        };
    }
}

加载全部内容