C语言汉诺塔公式

汉诺塔公式

汉诺塔问题在数学层面的公式：

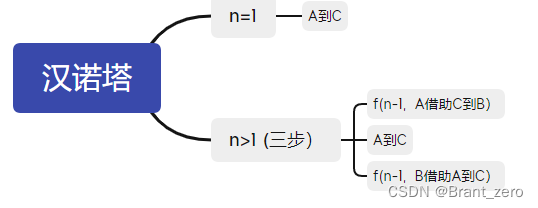
不用说，你看到这个公式一定一脸懵逼，我现在来讲解这个公式的作用。

先来回想一下大象放冰箱要几步，三步吧，打开冰箱，放进去，关上门就行了，我们先不要去思考一些细碎的步骤，将一个复杂的问题先简单化，再慢慢去分析。

那汉诺塔问题也是同样的简单三步：（假设有n个盘子）

一、把最大的盘子留在A柱，然后将其他的盘子全放在B柱。

二、把最大的盘子放到C柱。

三、然后将B柱上的所有盘子放到C柱。

这就是汉诺塔的流程，汉诺塔的精髓就是上面三句话。

n层汉诺塔有（2^n-1）次移动，来将盘子全部从A盘到C盘.

C语言递归公式

相应我们可以写出对应的C语言递归公式：（n就是盘子的个数，xyz就是柱子的名字）

相信你肯定有很多疑问，我们现在先来举几个例子再解释问题吧。

 一个盘子就不说了，因为最大的盘子就是他，所以他直接就去C盘了。

两层汉诺塔

共三步：把最大盘上面的全部放到B，然后最大盘去C，再把剩余的盘全部放到C就行了。

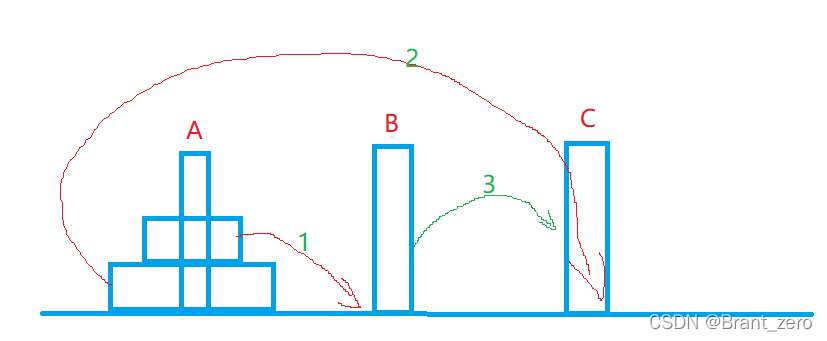
这是两个盘，共移动三次就移动完了，那三个盘呢？

三层汉诺塔

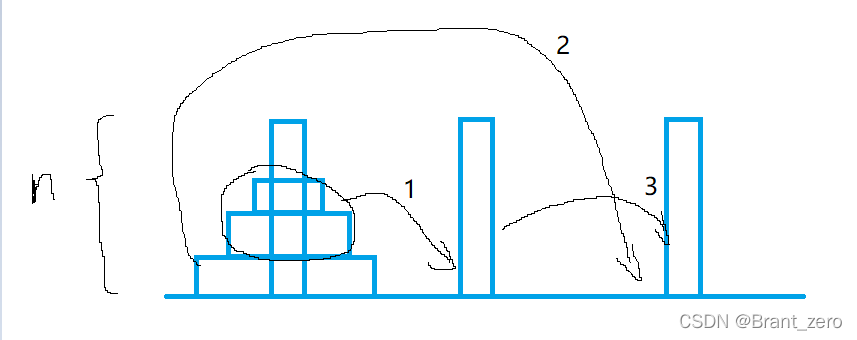
 把全部过程堪称一个整体，最大盘上面的所有盘全部看成一个整体，我们也只用执行三个步骤，我们要利用把大事化小的观点，不要一上来就思考具体是怎么移动的，这样看不清问题的本质。

我们再来具体分析三步具体要怎么移动.

第一步中，我们要移动三次，分别是A->C、是A->B、C->B这就是一大次完整的移动，在这一步中，我们套用了上一次的汉诺塔公式进行使用，这就是汉诺塔的难点，接下来我给大家看个图，希望大家能理解，（n是层数，X,Y,Z则是函数参数)

 汉诺塔的内部其实就像一个金字塔一样，其实每一次调用自己，就是按照上面所说精髓的公式调用自己，让自己的参数发生了变化。我希望大家能够自己去照着画一下流程，

第二步：将A到C，这就是将上图的第二步那写上第四次移动：A->C。

第三步，将B柱上的全部盘子借助A放到C

第七步完成后就会发现没有要执行的语句了，汉诺塔函数就结束返回到main函数了，自此求解汉诺塔函数的步骤就完成了。

好的，这样，我们移动三层汉诺塔的过程的就完成了，三次汉诺塔完成就算是解决了这个问题，因为即使盘子再多也就是一样的公式套用而已，明白两层和三层汉诺塔的运行原理就可以了，再多层的塔也是相同的流程。不难发现，递归就是让数学公式在C语言中体现了出来，让问题变的十分”简单“。

剩下就是了程序的主函数部分了，这个问题的主函数就很简单，主函数只用传来盘子的数量和三个柱子的名字就行了；代码如下

#include <stdio.h>
void change (char x,char y)     //打印盘子移动轨迹的函数
{
    printf("%c->%c\n", x, y);
}
void f(n, x, y, z)              //汉诺塔函数
{
    if (n == 1)
    {
        change(x, z);
    }
    else
    {
        f(n - 1, x, z, y);      //公式一：将A柱最大盘外的盘子借助C柱移到B柱
            change(x, z);       //公式二：将A上最大盘移动到C柱
        f(n - 1, y, x, z);      //公式三：将B柱上的盘借助A全部放到C柱
    }
}
int main()
{
    int m;
    scanf("%d", &m);
    f(m, 'A', 'B', 'C');
}

总结