C语言二叉树的后序遍历

时间:2022-05-23 guo5411 人气:0

首先我们从两个方面讲解二叉树的后序遍历(递归+迭代)

一.二叉树的后序遍历.(递归)

思想:

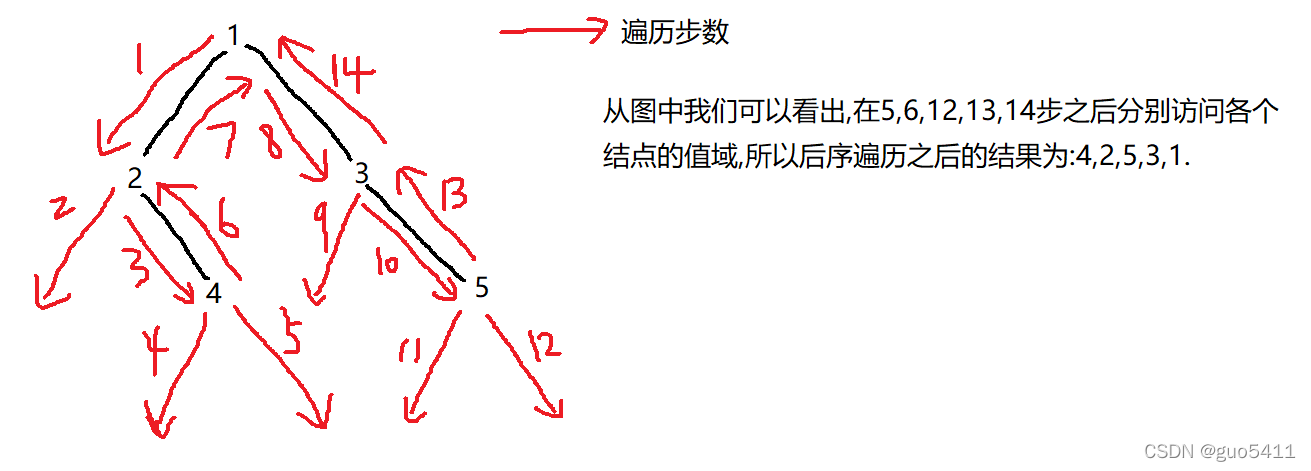
首先我们从二叉树的根节点开始先遍历其左孩子,①接着同样继续遍历其左孩子的左孩子,直到某个左孩子节点的左孩子为NULL时,②开始遍历其右孩子,如果其为NULL则访问该节点的值域,并返回其双亲节点重复第二步的操作,如果其不为NULL则以该节点为根节点重复第一步的操作.直到访问完所有节点时结束递归.

代码:

void BTreePostOrder(struct TreeNode* root,int* arry,int* Size){//后序遍历
    if(NULL==root){//递归出口
        return;
    }
    BTreePostOrder(root->left,arry,Size);//遍历左孩子
    BTreePostOrder(root->right,arry,Size);//遍历右孩子
    arry[(*Size)++]=root->val;//访问该节点
}

运行过程:(如图)

二.二叉树的后序遍历(迭代)

我们应该知道二叉树的前中后序遍历使用递归非常的简单,但是如果用迭代的话就比较有难度了,因此我思考了很久有没有一种迭代类型的算法与递归的框架相似(递归的三种算法框架非常相似只要会一个其他的便很好写出来),我们是否可以写出一种迭代算法:只用改变访问结点的次序便可以在迭代的方式下实现二叉树的前中后序遍历,因此我们使用数据结构中栈来模仿递归的形式实现了二叉树的前序遍历(在进栈时访问结点值域),中序遍历(在出栈时访问结点的值域),这种方法可以在同一种框架中实现迭代层面二叉树的前序遍历和中序遍历,但是到了后序遍历就没办法了,之后经过思考前序遍历与后序遍历的关系从而实现了同一种框架中实现前中后序遍历的迭代算法.

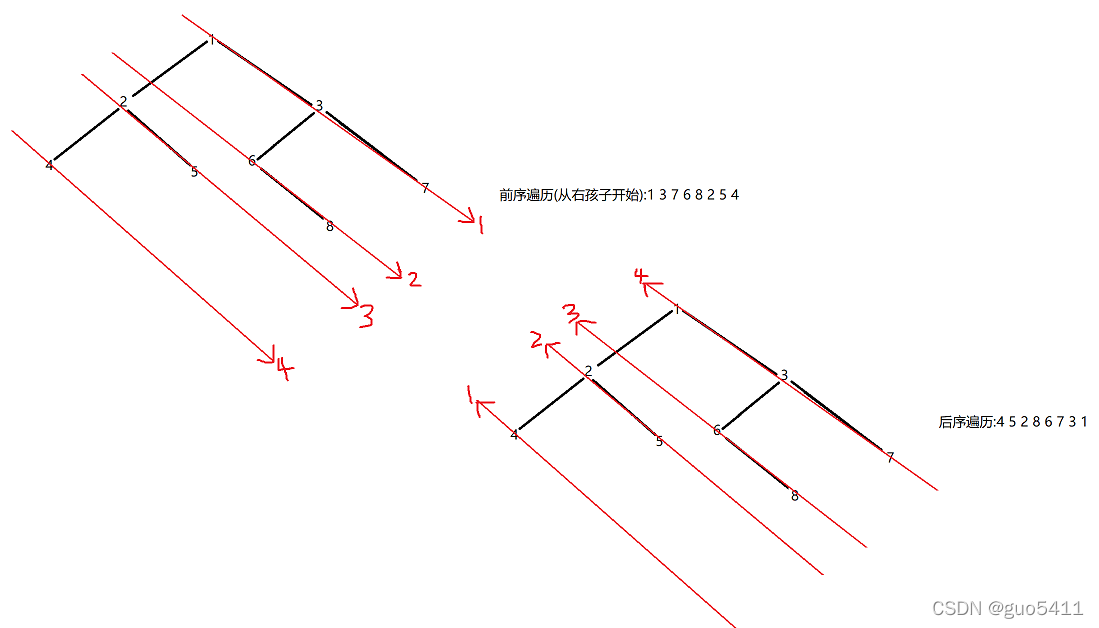
1.相信很多人在刚学习二叉树时都遇到过这种问题,选择题给定一颗二叉树,让我们给出二叉树的前中后序遍历的节点顺序.(每个人都有自己的计算方法),下面说一下我的计算方法.

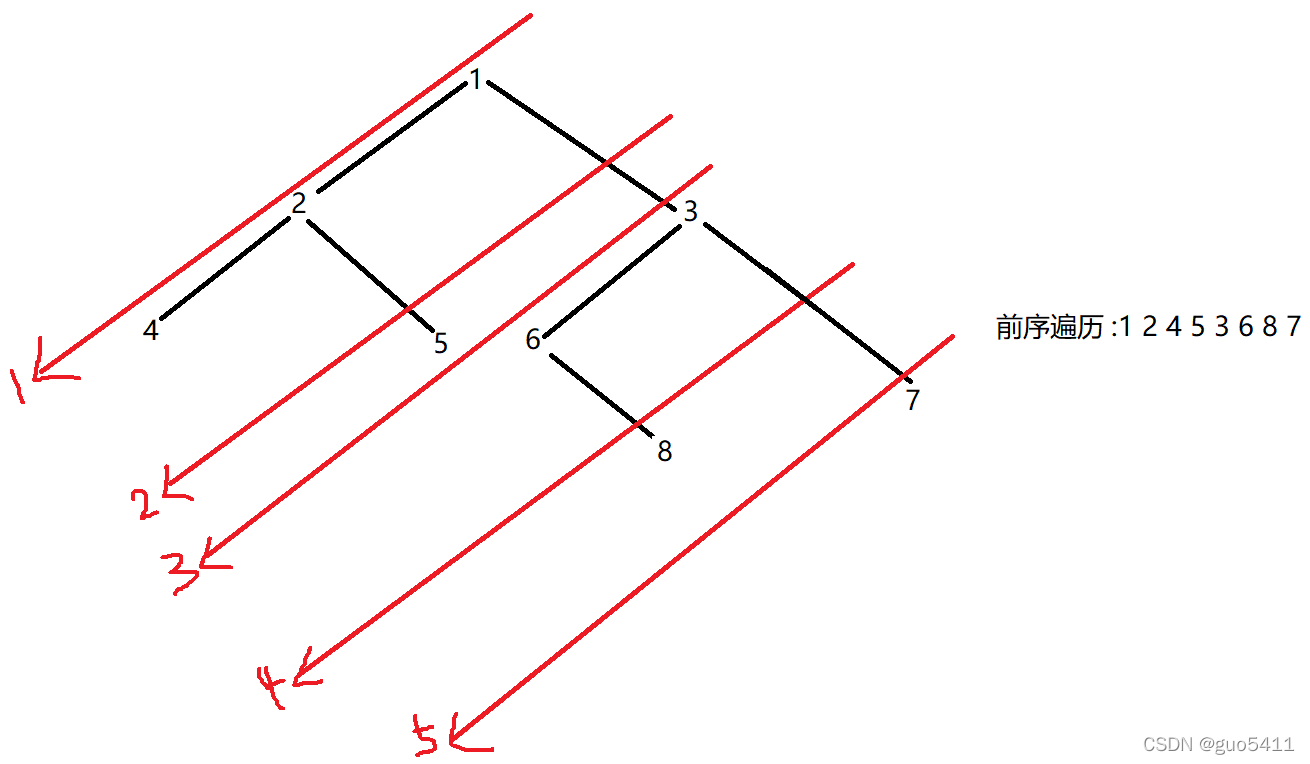
前序:我们按图中红色箭头的顺序和其指向依次读取箭头上的结点便可得到其前序遍历.

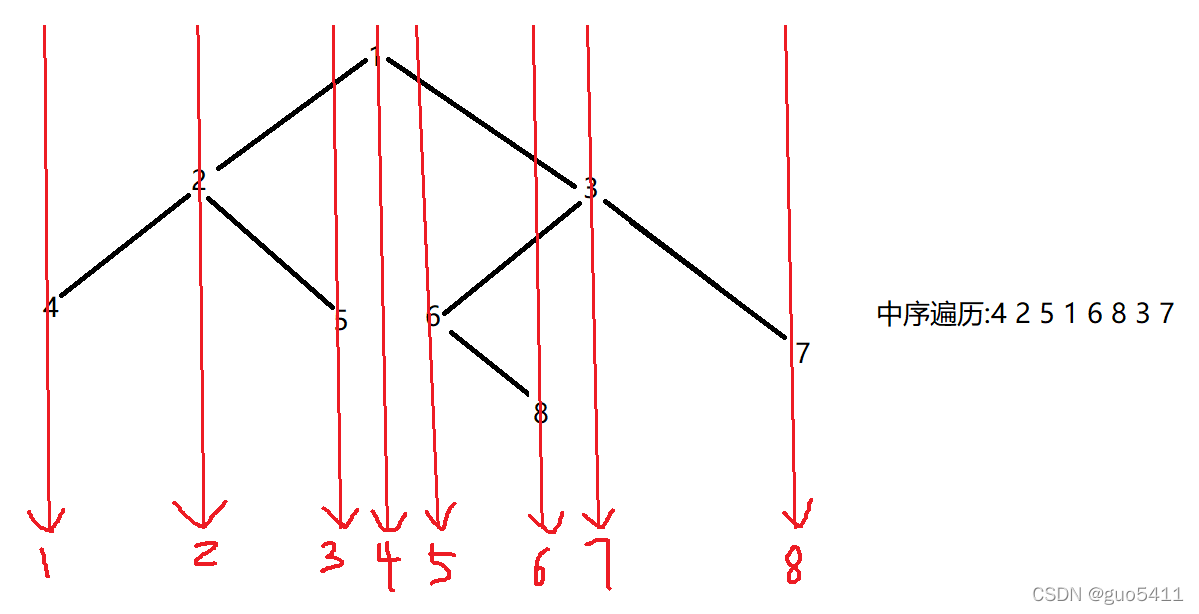
中序:我们按图中红色箭头的顺序和其指向依次读取箭头上的结点便可得到其中序遍历.

后序:我们按图中红色箭头的顺序和其指向依次读取箭头上的结点便可得到其后序遍历.

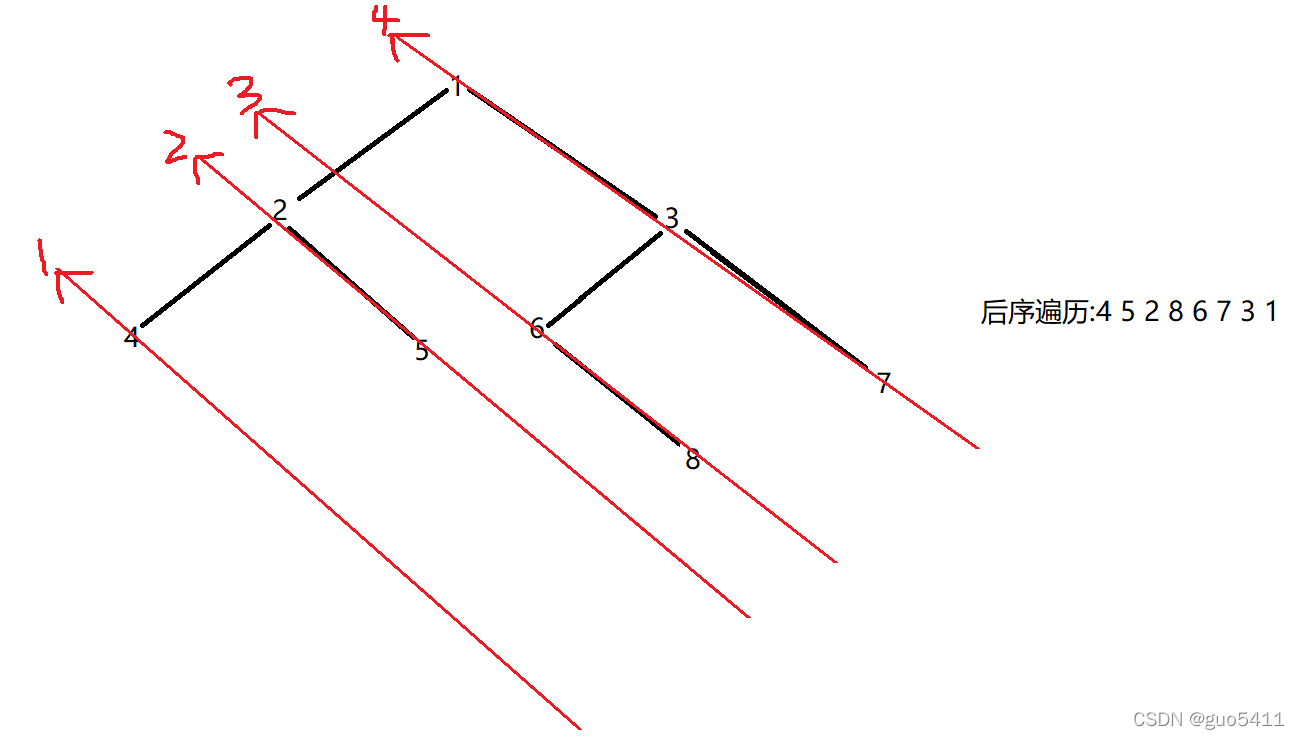
经过上图我们可以看出二叉树的后序遍历刚好与从右孩子开始的前序遍历所得到的的值完全相反.因此我们可以使用前序遍历的代码从右孩子开始进行前序遍历,最后将得到的值反向打印即可.

代码:

typedef struct TreeNode BTNode;
 
typedef struct Stack{//栈的结构体
    BTNode* array[100];
    int size;
}Stack;
 
void StackPush(Stack* a,BTNode* root){//入栈
    a->array[(a->size)++]=root;
}
 
void StackPop(Stack* a){//出栈
    (a->size)--;
}
 
void Reverse(int* a,int Long){//反向打印
    int left_1=0;
    int right_1=Long-1;
    while(left_1 < right_1){
        int temp=a[left_1];
        a[left_1]=a[right_1];
        a[right_1]=temp;
        left_1++;
        right_1--;
    }
}
 
int* postorderTraversal(struct TreeNode* root, int* returnSize){//从右孩子开始的前序遍历
    int* b=(int*)malloc(sizeof(int)*100);
    if(NULL==b){
        printf("申请节点失败!\n");
        return NULL;
    }
    Stack a;
    a.size=0;
    BTNode* root_temp;
    int i=0;
    StackPush(&a,root);
    while(NULL != a.array[a.size-1]){
        b[i++]=a.array[a.size-1]->val;
        StackPush(&a,a.array[a.size-1]->right);
        while(NULL == a.array[a.size-1]){
            StackPop(&a);
            if(0 == a.size){
                Reverse(b,i);           
                (*returnSize)=i;
                return b;
            }
            root_temp=a.array[a.size-1];
            StackPop(&a); 
            StackPush(&a,root_temp->left);
        }
    }
    Reverse(b,i);
    (*returnSize)=i;
    return b;
}

从右孩子开始的前序遍历:正常的前序遍历是先访问节点,然后遍历其左孩子,再遍历其右孩子.而该前序遍历是先访问节点,然后遍历其右孩子,再遍历其左孩子.

代码:

void BTreeInOrder(struct TreeNode* root,int* arry,int* Size){//前序遍历
    if(NULL==root){//递归出口
        return;
    }
    arry[(*Size)++]=root->val;//访问该节点
    BTreeInOrder(root->right,arry,Size);//遍历右孩子
    BTreeInOrder(root->left,arry,Size);//遍历左孩子
}

具体比较如图:

总结

加载全部内容