C语言函数递归
Catzzz666 人气:0什么是递归?
递归(recursion):程序调用自身的一种编程技巧。
如何理解函数递归:
1.从调用自身层面:函数递归就是函数自己调用自己。
2.从编程技巧层面:一种方法(把一个大型复杂的程序转换为一个类似的小型简单的程序),这种方法的主要思想就是把大事化小。
递归的两个必要条件
1.存在限制条件,当满足这个限制条件时,递归便不再继续。
2.每次递归调用之后越来越接近这个限制条件。
递归实例
实例1(按照顺序打印一个数的整形值)
参考代码(可以先去尝试是否可以解决问题)

画图讲解

注意:在每次打印后都有一个空格。
程序运行结果

完整代码
#include <stdio.h>
void print(int n)
{
if(n>9)
{
print(n/10);
}
printf("%d ", n%10);
}
int main()
{
int num = 1234;
print(num);
return 0;
}实例2 (使用函数在不创建变量的情况下求字符串长度)
参考代码
画图讲解
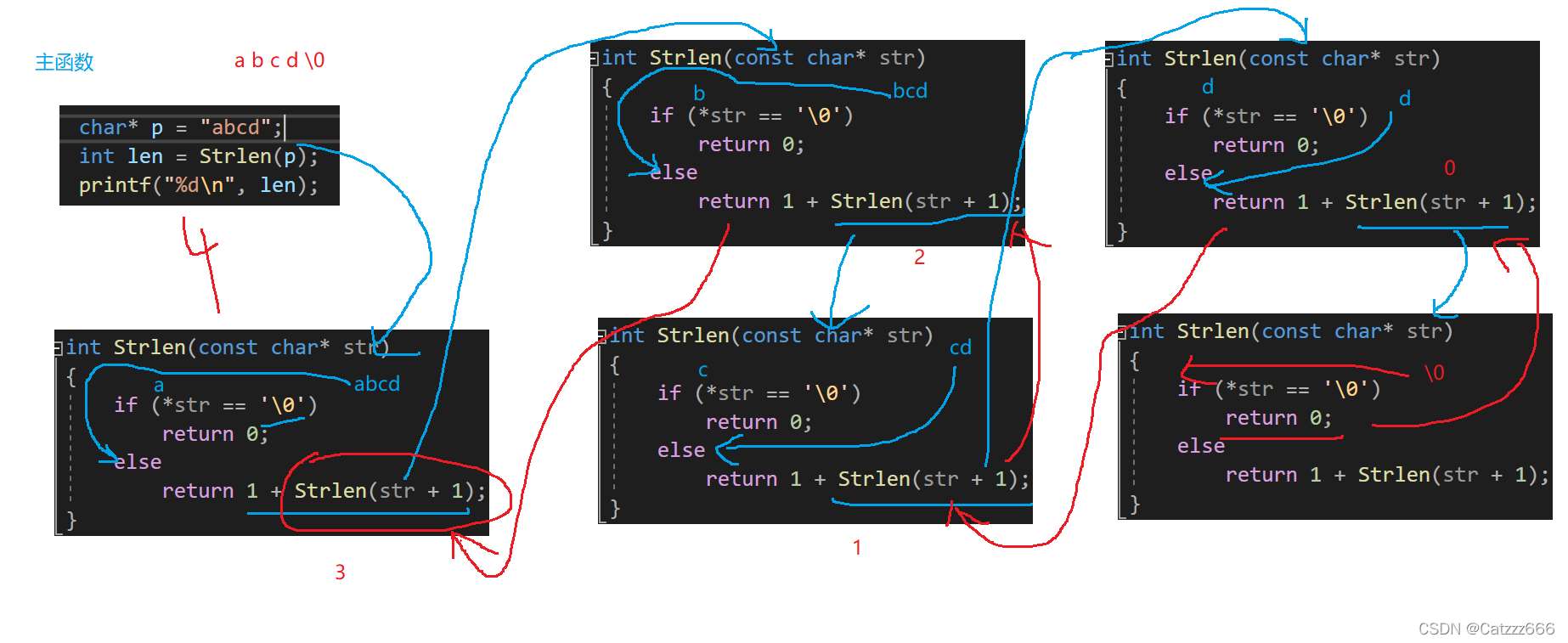
程序运行结果
完整代码
#include <stdio.h>int Strlen(const char* str){if (*str == '\0')return 0;elsereturn 1 + Strlen(str + 1);}int main(){char* p = "abcd";int len = Strlen(p);printf("%d\n", len);return 0;}递归与迭代
迭代是重复反馈过程的活动,其目的通常是为了逼近所需目标或结果。 每一次对过程的重复称为一次“迭代”,而每一次迭代得到的结果会作为下一次迭代的初始值。 目前对于c语言来说,迭代可以简单认为是循环结构。
对于递归与迭代,我们同样通过两个实例来理解:
实例1 (求n的阶乘)
方法一(使用递归)
参考代码
通过数学方法讲解
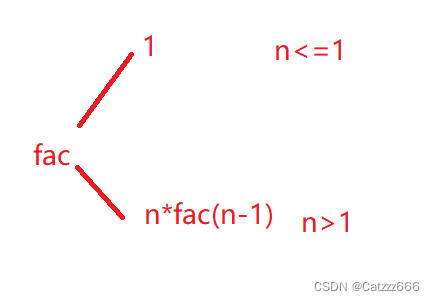
完整代码
#include <stdio.h>
int fac(int n)
{
if (n == 1)
return 1;
else
return n * fac(n - 1);
}
int main()
{
int n = 0;
scanf("%d", &n);
int ret = fac(n);
printf("%d\n", ret);
return 0;
}方法二(使用迭代)
完整代码
#include <stdio.h>
int main()
{
int n = 0;
scanf("%d", &n);
int i = 0;
int ret = 1;
for (i = 1; i <= n; i++)
{
ret *= i;
}
printf("%d\n", ret);
return 0;
}运行结果
实例2 (求解斐波那契数列)
斐波那契数列:指的是这样一个数列:1、1、2、3、5、8、13、21、34、……在数学上,斐波纳契数列以如下被以递归的方法定义:F(1)=1,F(2)=1, F(n)=F(n-1)+F(n-2)(n>=2,n∈N*)
方法一 (递归求解)
参考代码
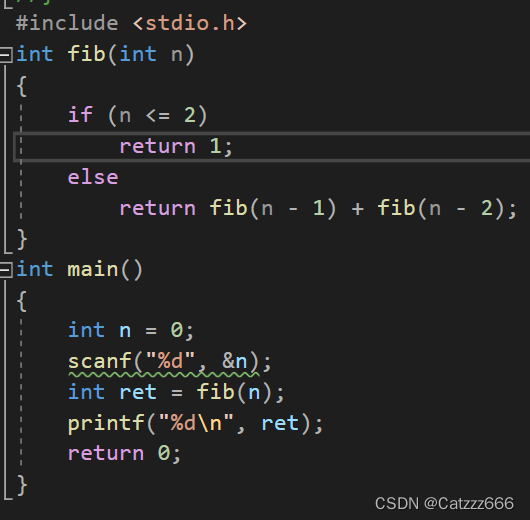
通过数学方法求解
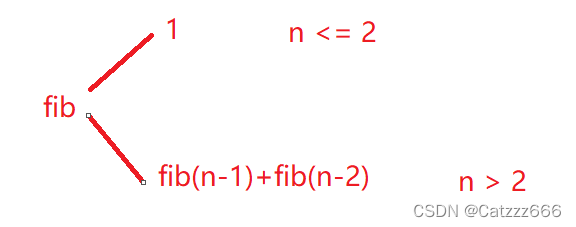
运行结果

完整代码
#include <stdio.h>
int fib(int n)
{
if (n <= 2)
return 1;
else
return fib(n - 1) + fib(n - 2);
}
int main()
{
int n = 0;
scanf("%d", &n);
int ret = fib(n);
printf("%d\n", ret);
return 0;
}注意:当求得的数字较大时,使用递归的方法计算机所要计算的量是相当大的,因为每次计算一个第n项时都需要计算第n-1项和第n-2项 ,这里我们通过求解第40项来观察fib(3)的计算次数来观察。
运行结果
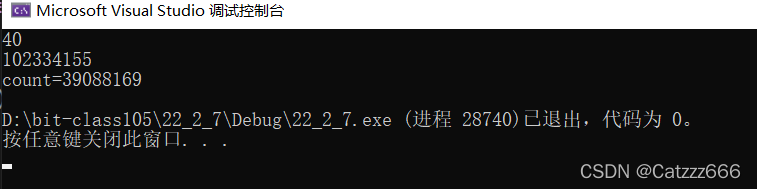
计算第40项时已经计算第3项已经有三千多万次,那么如果计算第一百项,一千项...时程序就会崩溃...这是我们就要考虑使用迭代的方法进行求解。
方法二(迭代求解)
参考代码 (主函数不变)

画图讲解

完整代码
#include <stdio.h>
int fib(int n)
{
int a = 1;
int b = 1;
int c = 1;
while (n > 2)
{
c = a + b;
a = b;
b = c;
n--;
}
return c;
}
int main()
{
int n = 0;
scanf("%d", &n);
int ret = fib(n);
printf("%d\n", ret);
return 0;
}运行结果
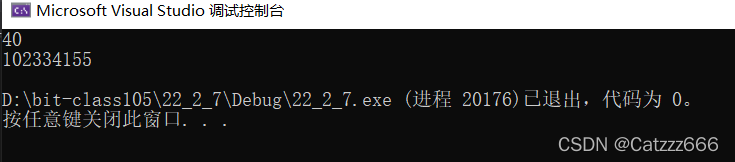
这里我们可以看出递归和迭代的运行结果是一样的,但是迭代的运行速度要更快。
这时候我们会想:
为什么有时候用递归简便,而有时候用迭代简便呢?
注意:
1.许多问题是以递归的形式进行求解的,这只是因为它比非递归的形式更加清晰。
2.但是这些问题的迭代实现往往比递归实现效率更高,虽然可读性差些。
3.当一个问题相当复杂时,此时递归实现的简洁性便可以弥补它所带来的运行开销。
总结
本篇文章就到这里了,希望能够给你带来帮助,也希望您能够多多关注的更多内容!
加载全部内容