Java 栈和基础队列
Word码鸭 人气:0栈和队列:都是线性表,都是基于List基础上的实现
线性表:数组,链表,字符串,栈,队列
元素按照一条“直线”排列,线性表这个结构中,一次添加单个元素
栈(stack)
一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶,另一端称为栈底。栈中的数据元素遵守后进先出LIFO(Last In First Out)的原则。
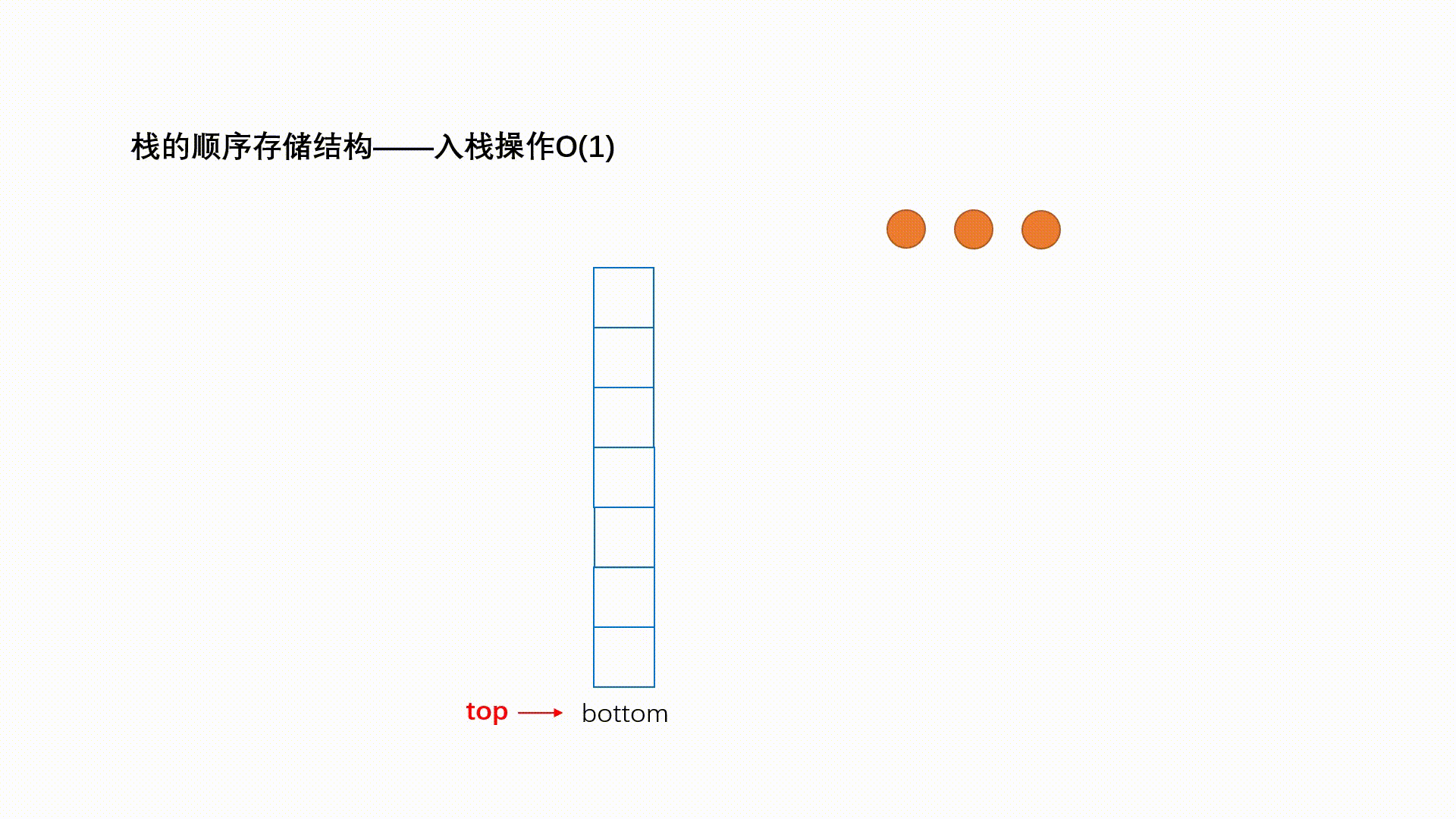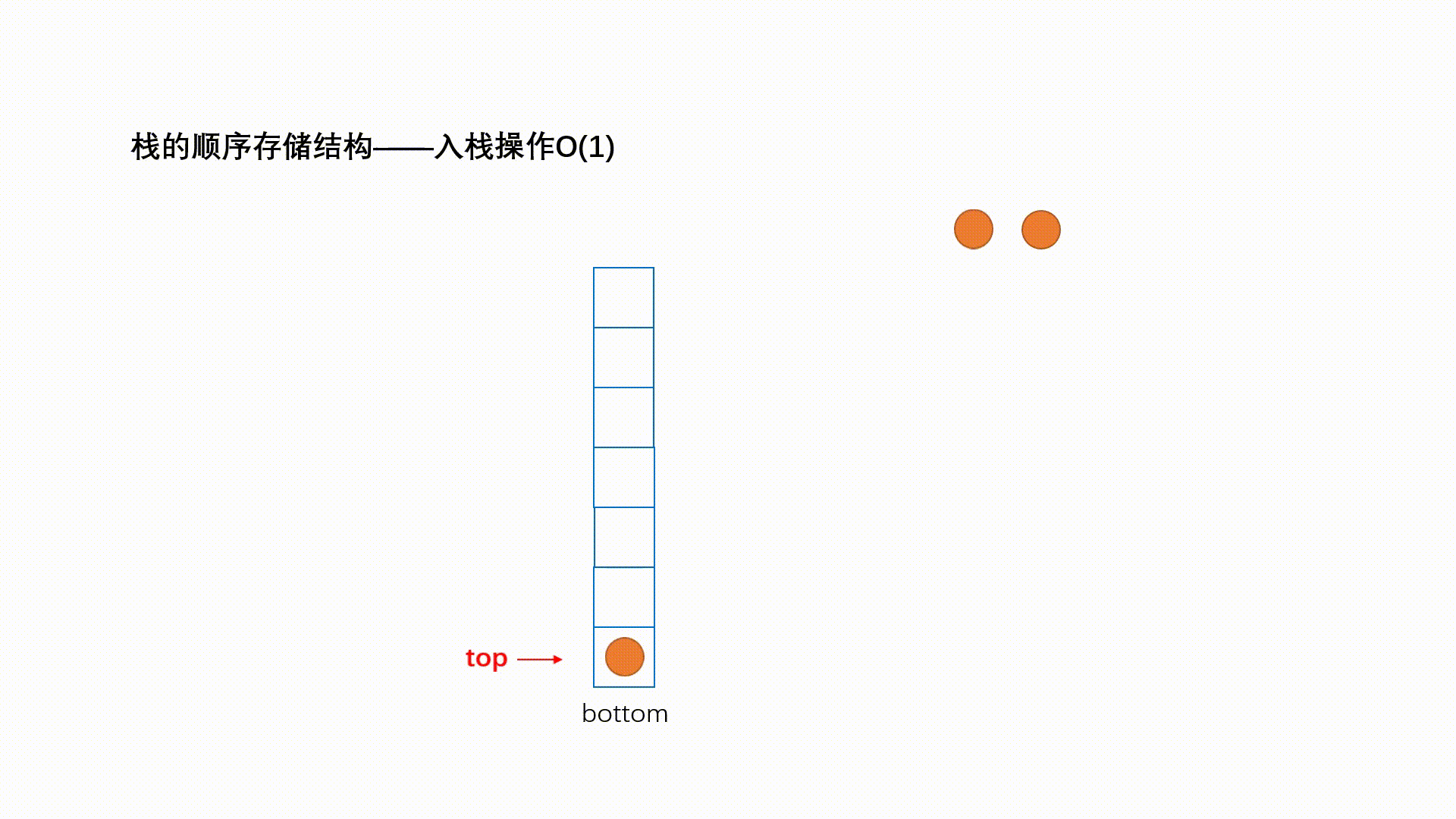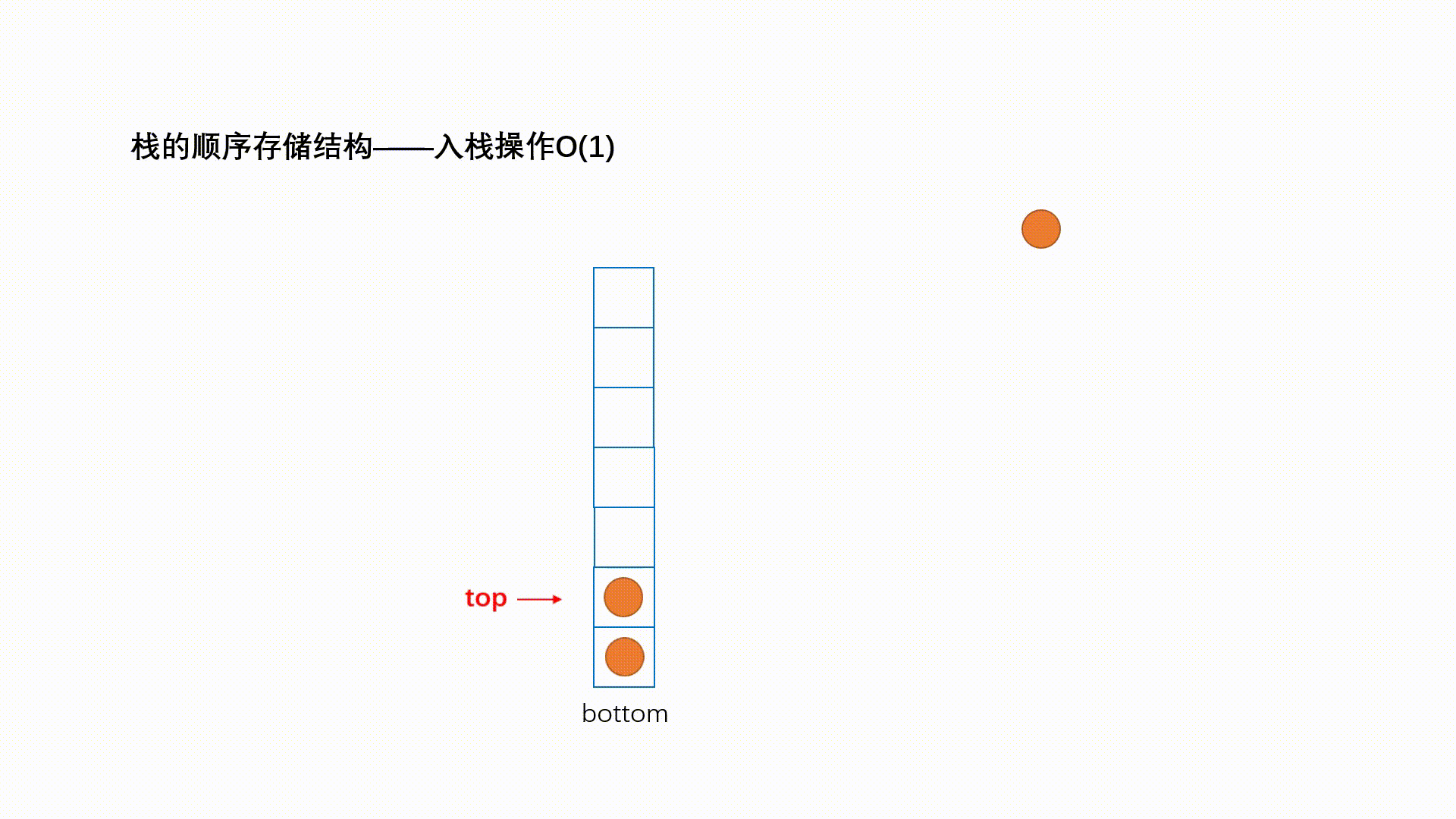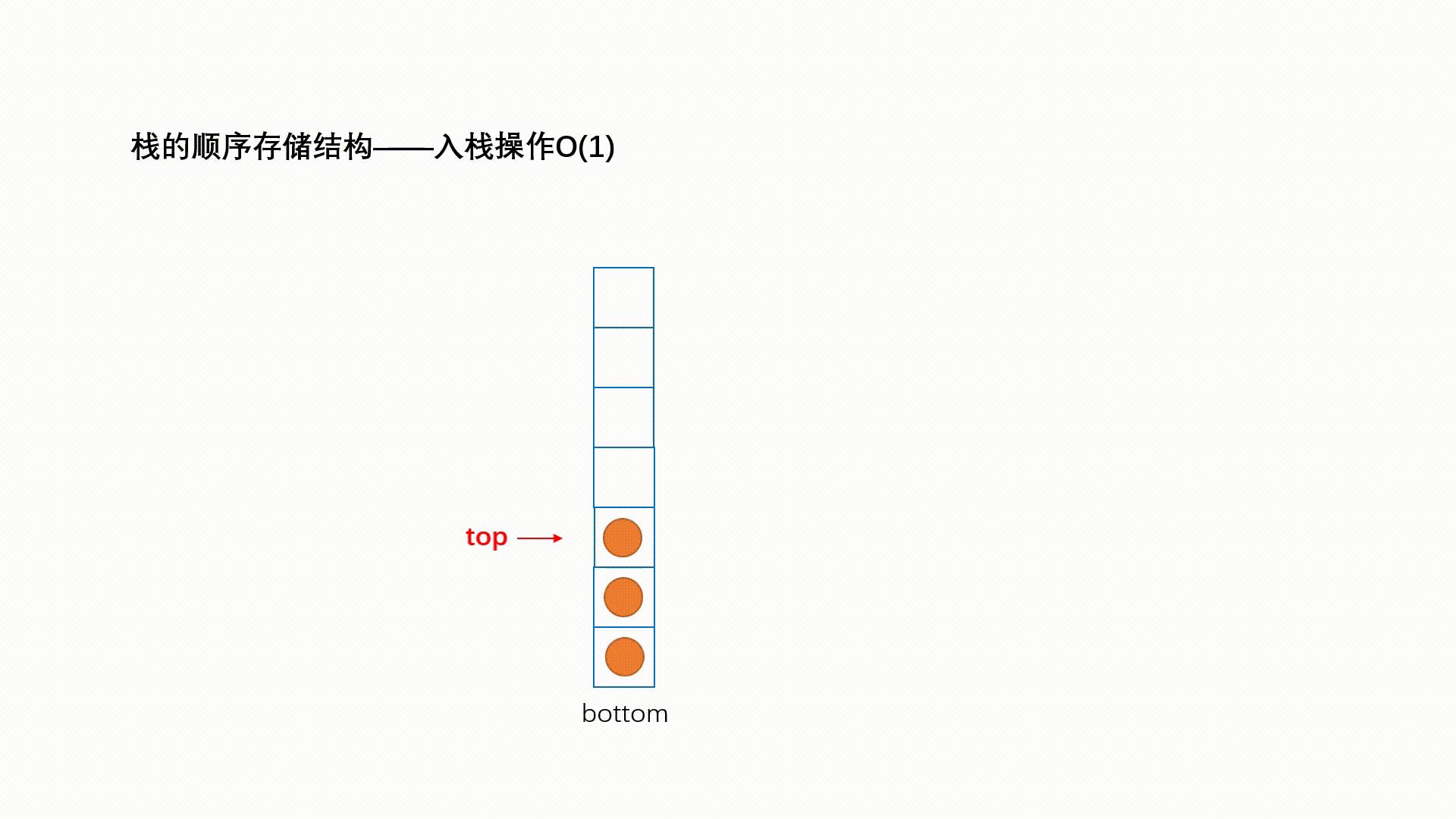
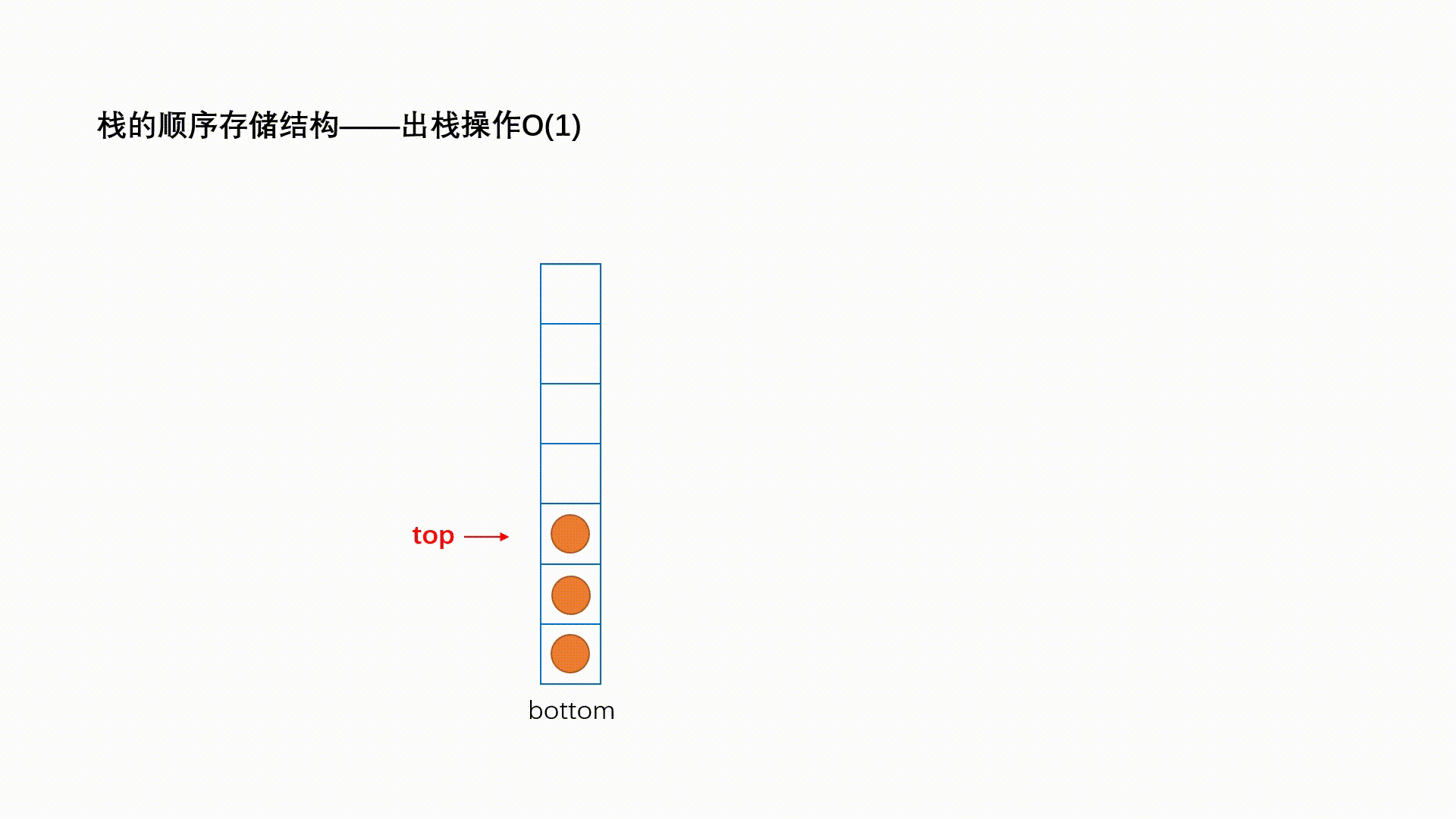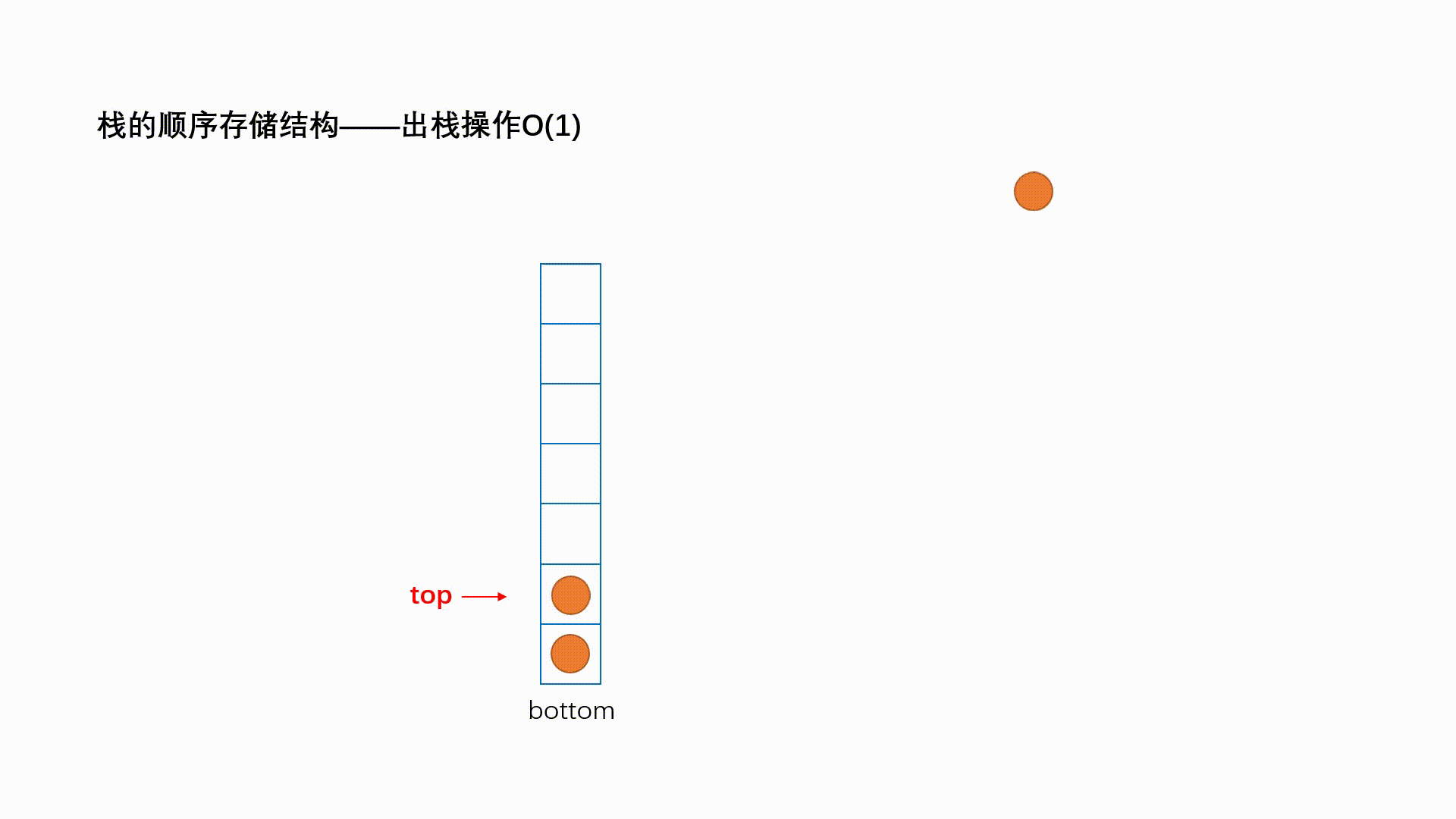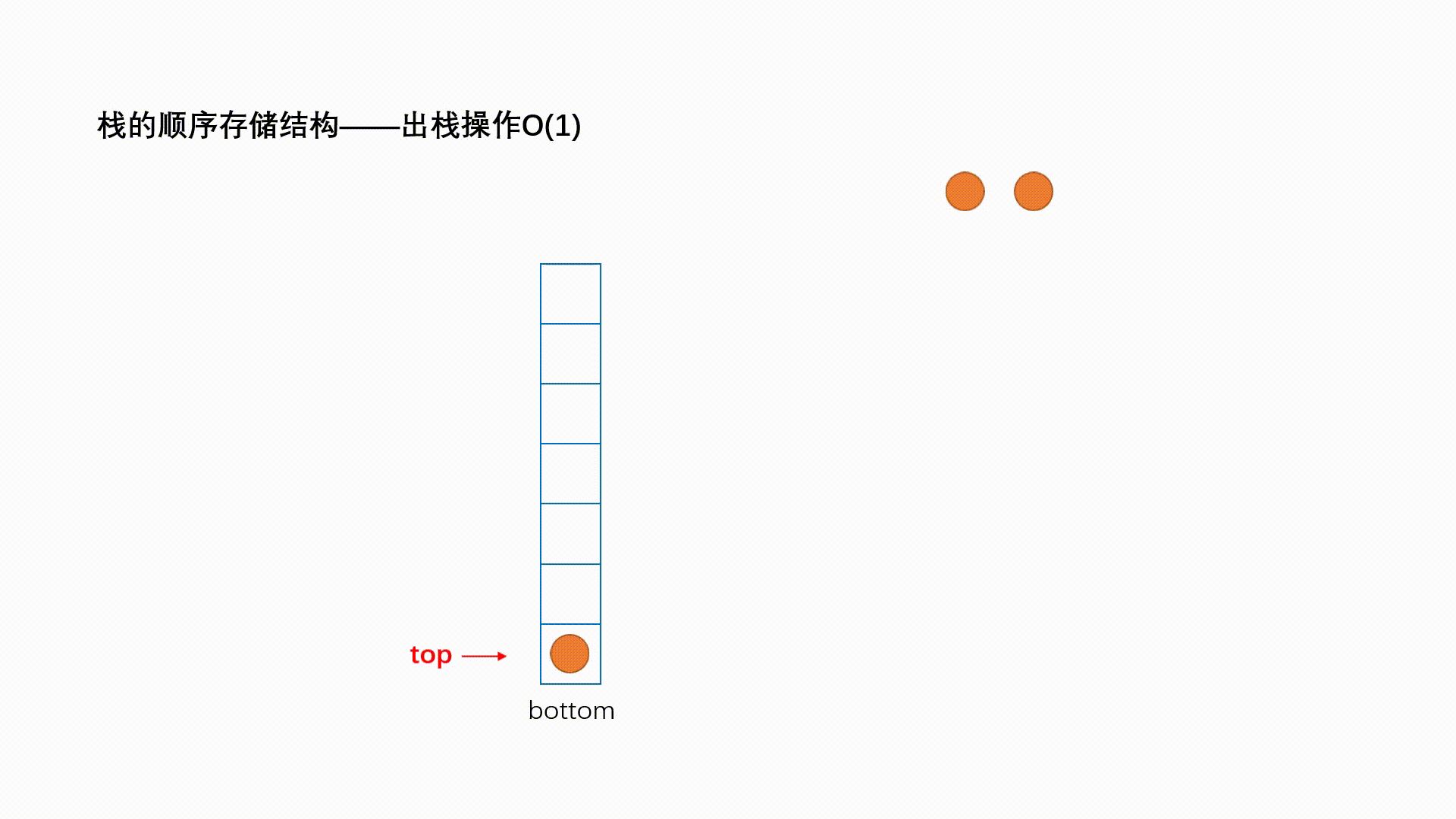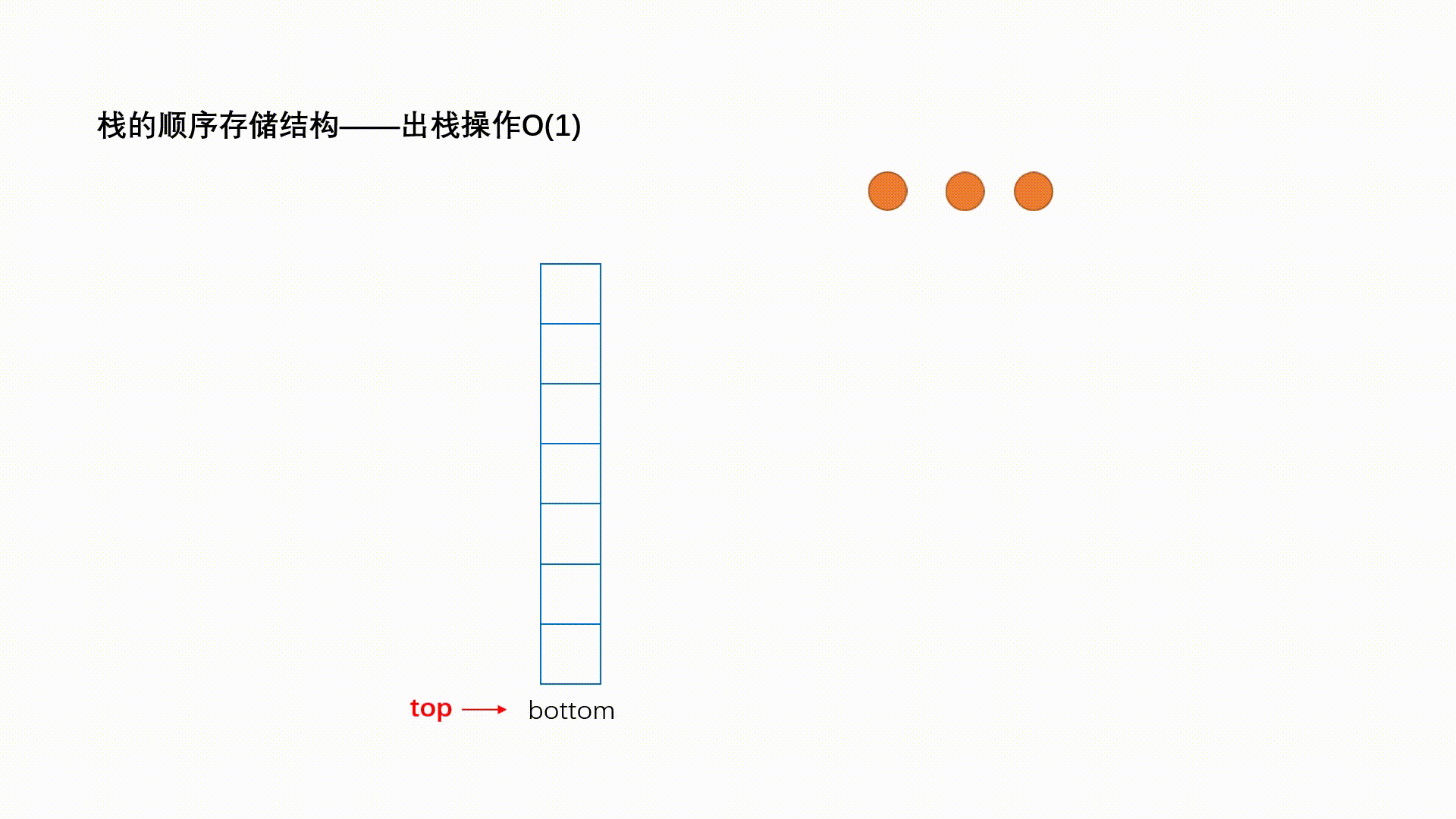
栈支持的三个核心操作:
- 入栈push
- 出栈pop
- 返回栈顶元素peek
栈的常见实际应用:
- 无处不在的撤销操作undo,一般任意的编辑器都使用 ctrl + z 操作,其实本质就是每次操作一次 ctrl + z 就是一次栈的pop
- 浏览器的前进后退,浏览器维护了一个栈结构A->B->C,此时页面停留在C,想要回到页面B,点击后退键头就相当于将C出栈,此时的栈顶就是B
- 在开发程序中的“调用栈”操作系统栈底层就是栈的实现

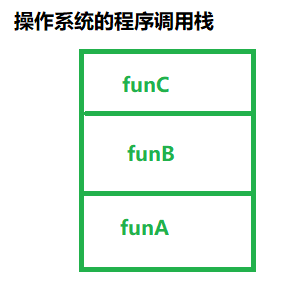
栈的实现
栈是一种线性表,所以实现它即可使用数组,也可以使用链表
- 基于数组实现的栈—顺序栈(栈顶实际就是数组尾部,在数组尾部添加和删除)
- 基于链表实现的栈—链式栈(链表的头插和尾插)
在数组尾部进行删除和插入的时间复杂度为O(1),所以用数组实现栈是我们的首选
实现代码:
//基于数组实现的栈
public class MyStack<E> {
private int size;//数组长度
//实际存储数据的动态数组
private List<E> data = new ArrayList<>();
//入栈,默认尾插
public void push(E val){
data.add(val);
size ++;
}
//弹出栈顶元素,返回栈顶的值
public E pop(){
if(isEmpty()){
//栈为空
throw new NoSuchElementException("stack is empty!cannot pop!");
}
//删元素
E val = data.remove(size-1);
size--;
return val;
//上面三句等同于return data.remove(size-1);
}
//返回栈顶元素,但不出栈
public E peek(){
if(isEmpty()){
throw new NoSuchElementException("stack is empty!cannot peek");
}
return data.get(size-1);
}
// 判断当前栈是否为空
public boolean isEmpty() {
return size == 0;
}
public String toString() {
StringBuilder sb = new StringBuilder();
sb.append("[");
for (int i = 0; i < size; i++) {
sb.append(data.get(i));
if (i != size - 1) {
// 此时还没到栈顶,还没到数组末尾
sb.append(", ");
}
}
sb.append("] top");
return sb.toString();
}
}
//--------------------------
//测试类·
public class StackTest {
public static void main(String[] args) {
MyStack<Integer> myStack = new MyStack<>();
myStack.push(1);
myStack.push(3);
myStack.push(5);
System.out.println(myStack);
System.out.println(myStack.pop());//删除栈顶
System.out.println(myStack.peek());//输出栈顶,此时栈顶为3
System.out.println(myStack.isEmpty());
}
}
//输出结果:
[1, 3, 5] top
5
3
false
队列
只允许在一端进行插入数据操作,在另一端进行删除数据操作的特殊线性表,队列遵循先进先出FIFO(First In First Out)的原则 :进行插入操作的一端称为队尾(Tail/Rear) 出队列:进行删除操作的一端称为队头
其实队列的定义很简单,就相当于我们现实生活的排队购物,先排队的人先结账,也就先离开
队列的子类比栈要复杂一些,它有:
- 基础队列—FIFO
- 基于优先级的队列—按照优先级大小出队
- 循环队列—基于数组实现的
- 双端队列
无论是哪种队列,都必须支持三个核心操作:
- 入队—offer
- 出队—poll
- 返回队首元素—peek
基础队列的实现
- 基于数组实现的队列—顺序队列
- 基于链表实现的队列—链式队列
由于队列是从队尾插入,队首出队,而在数组头部删除的时间复杂度为O(n),此时我们用链表会更好一些。而且无论实现哪种队列都需要覆写三个基本操作,因此我们将队列设计为接口
实现代码:
public interface Queue<E> {
// 入队
void offer(E val);
// 出队
E poll();
// 返回队首元素
E peek();
// 判断队列是否为空
boolean isEmpty();
}
//基于链表实现的基础队列
public class MyQueue<E> implements Queue<E> {
// 链表的每个节点
// ------------------------------
//内部类
private class Node {
E val;
Node next;
public Node(E val) {
this.val = val;
}
}
// ------------------------------
// 当前队列中的元素个数
private int size;
// 队首
private Node head;
// 队尾
private Node tail;
@Override
public void offer(E val) {
Node node = new Node(val);
if (head == null) {
// 此时链表为空
head = tail = node;
}else {
tail.next = node;
tail = node;
}
size ++;
}
@Override
public E poll() {
if (isEmpty()) {
throw new NoSuchElementException("queue is empty!cannot poll!");
}
E val = head.val;
Node node = head;
head = head.next;
// 将原来头节点脱钩
node.next = null;
size --;
return val;
}
@Override
public E peek() {
if (isEmpty()) {
throw new NoSuchElementException("queue is empty!cannot peek!");
}
return head.val;
}
@Override
public boolean isEmpty() {
return size == 0;
}
@Override
public String toString() {
StringBuilder sb = new StringBuilder();
sb.append("front [");
// 链表的遍历
for (Node x = head;x != null;x = x.next) {
sb.append(x.val);
if (x.next != null) {
// 还没走到链表尾部
sb.append(", ");
}
}
sb.append("]");
return sb.toString();
}
}
//测试类
public class QueueTest {
public static void main(String[] args) {
Queue<Integer> queue = new MyQueue<>();
queue.offer(1);
queue.offer(3);
queue.offer(5);
System.out.println(queue);
}
}作为初学者,我们不能小瞧任何简单的数据结构与算法,基础的数据结构往往作为高阶数据结构的一部分来应用,万丈高楼平地起,平时要多加练习,我们一起加油!
加载全部内容