Python实现堆排序 Python实现堆排序案例详解

Python实现堆排序

一、堆排序简介

堆排序(Heap Sort)是利用堆这种数据结构所设计的一种排序算法。

堆的结构是一棵完全二叉树的结构，并且满足堆积的性质：每个节点(叶节点除外)的值都大于等于(或都小于等于)它的子节点。

关于二叉树和完全二叉树的介绍可以参考：https:

堆排序先按从上到下、从左到右的顺序将待排序列表中的元素构造成一棵完全二叉树，然后对完全二叉树进行调整，使其满足堆积的性质：每个节点(叶节点除外)的值都大于等于(或都小于等于)它的子节点。构建出堆后，将堆顶与堆尾进行交换，然后将堆尾从堆中取出来，取出来的数据就是最大(或最小)的数据。重复构建堆并将堆顶和堆尾进行交换，取出堆尾的数据，直到堆中的数据全部被取出，列表排序完成。

堆结构分为大顶堆和小顶堆：

1. 大顶堆：每个节点(叶节点除外)的值都大于等于其子节点的值，根节点的值是所有节点中最大的，所以叫大顶堆，在堆排序算法中用于升序排列。

2. 小顶堆：每个节点(叶节点除外)的值都小于等于其子节点的值，根节点的值是所有节点中最小的，所以叫小顶堆，在堆排序算法中用于降序排列。

二、堆排序原理

堆排序的原理如下：

1. 将待排序列表中的数据按从上到下、从左到右的顺序构造成一棵完全二叉树。

2. 将完全二叉树中每个节点(叶节点除外)的值与其子节点(子节点有一个或两个)中较大的值进行比较，如果节点的值小于子节点的值，则交换他们的位置(大顶堆，小顶堆反之)。

3. 将节点与子节点进行交换后，要继续比较子节点与孙节点的值，直到不需要交换或子节点是叶节点时停止。比较完所有的非叶节点后，即可构建出堆结构。

4. 将数据构造成堆结构后，将堆顶与堆尾交换，然后将堆尾从堆中取出来，添加到已排序序列中，完成一轮堆排序，堆中的数据个数减1。

5. 重复步骤2,3,4，直到堆中的数据全部被取出，列表排序完成。

以列表 [10, 17, 50, 7, 30, 24, 27, 45, 15, 5, 36, 21] 进行升序排列为例。列表的初始状态如下图。

要进行升序排序，则构造堆结构时，使用大顶堆。

1. 将待排序列表中的数据按从上到下、从左到右的顺序构造成一棵完全二叉树。

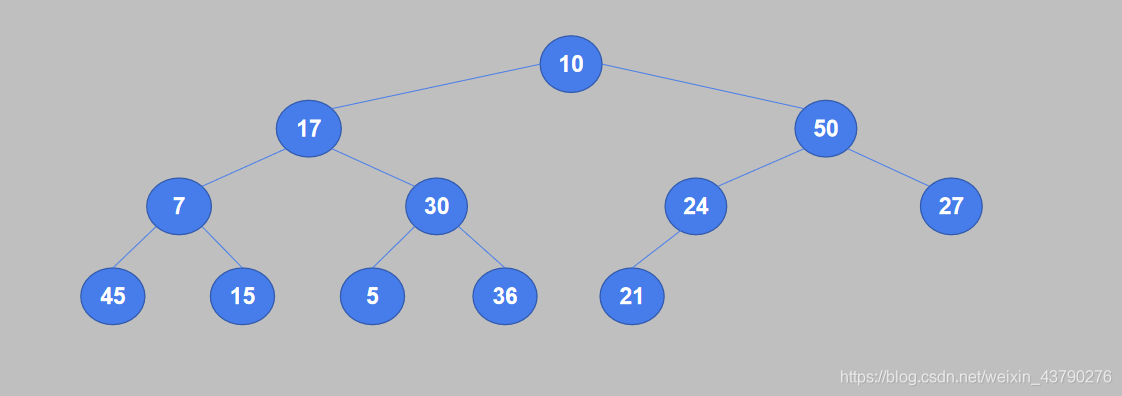
2. 从完全二叉树的最后一个非叶节点开始，将它的值与其子节点中较大的值进行比较，如果值小于子节点则交换。24是最后一个非叶子节点，它只有一个子节点21，24大于21，不需要交换。

3. 继续将倒数第二个非叶节点的值与其子节点中较大的值进行比较，如果值小于子节点则交换。节点30有两个子节点5和36，较大的是36，30小于36，交换位置。

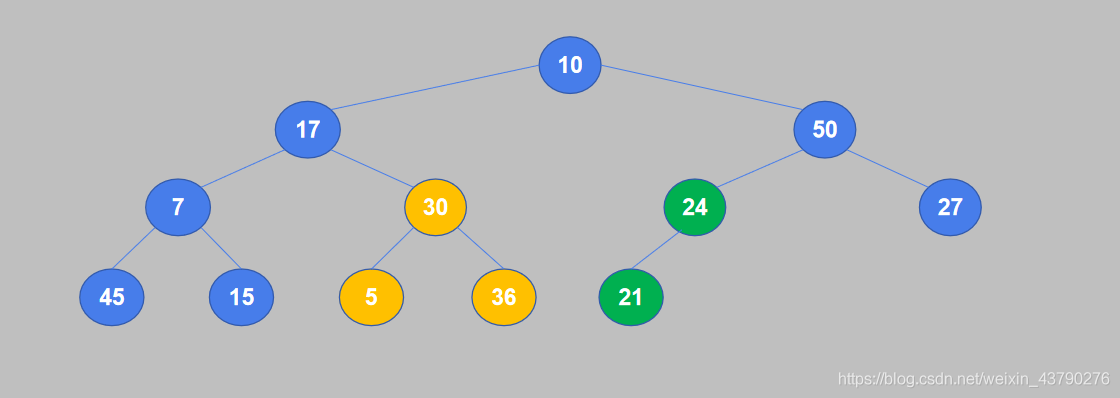
4. 重复对下一个节点进行比较。7小于45，交换位置。

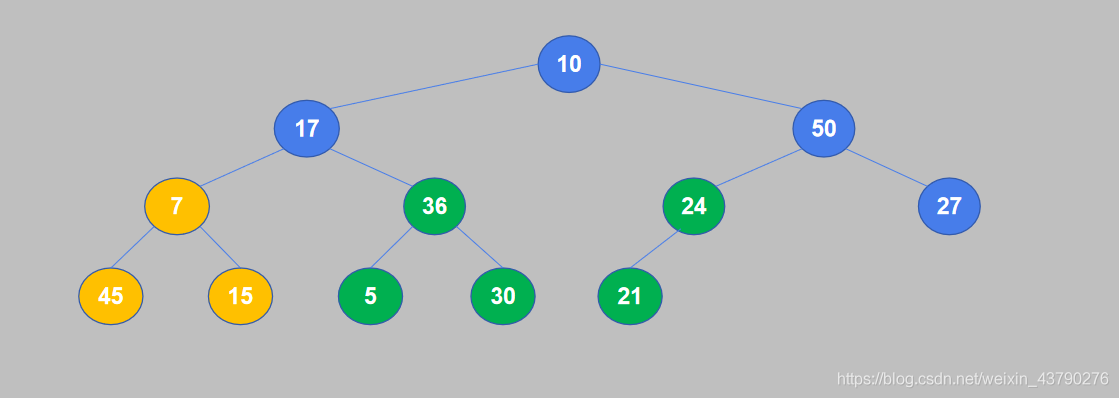
5. 继续重复，50大于27，不需要交换位置。如果不需要进行交换，则不用再比较子节点与孙节点。

6. 继续重复，17小于45，交换位置。

7. 17和45交换位置之后，17交换到了子节点的位置，还需要继续将其与孙节点进行比较。17大于15，不需要交换。

8. 继续对下一个节点进行比较，10小于50，交换位置。

9. 10和50交换位置之后，10交换到了子节点的位置，还需要继续将其与孙节点进行比较。10小于于27，交换位置。

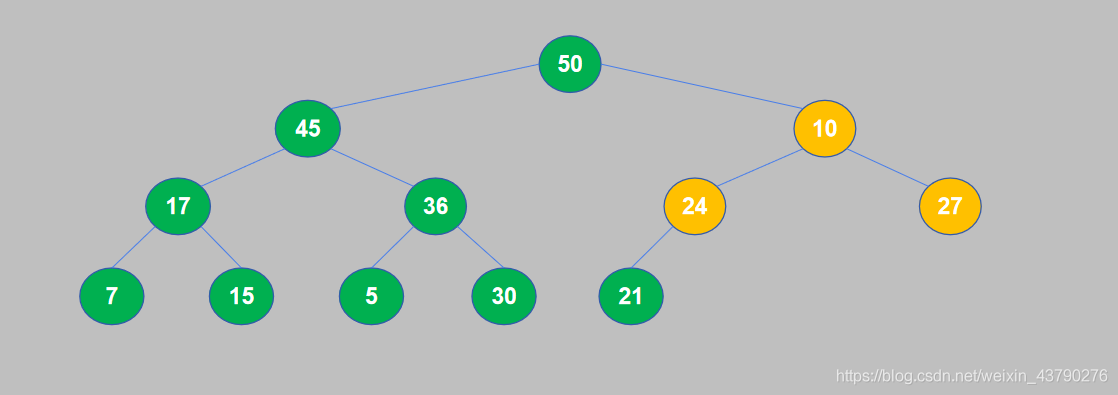
10. 此时，一个大顶堆构造完成，满足了堆积的性质：每个节点(叶节点除外)的值都大于等于它的子节点。

11. 大顶堆构建完成后，将堆顶与堆尾交换位置，然后将堆尾从堆中取出。将50和21交换位置，交换后21到了堆顶，50(最大的数据)到了堆尾，然后将50从堆中取出。

12. 将50从堆中取出后，找到了待排序列表中的最大值，50添加到已排序序列中，第一轮堆排序完成，堆中的元素个数减1。

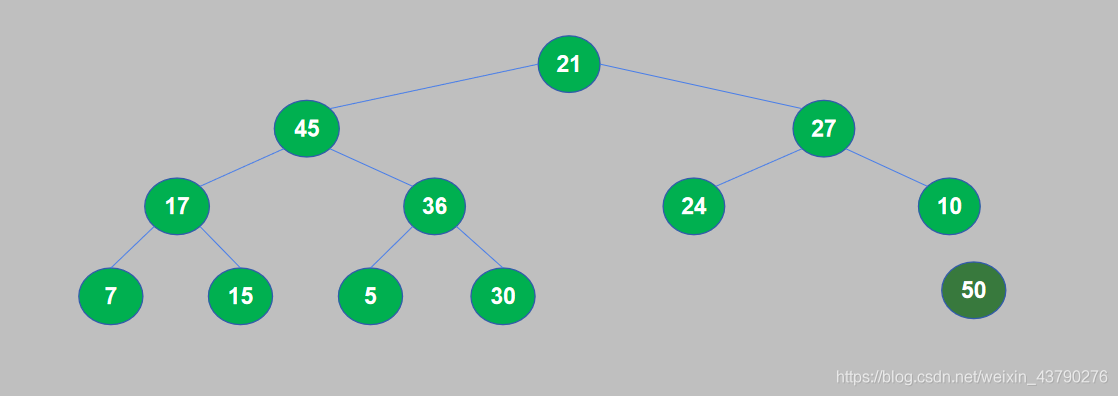
13. 取出最大数据后，重复将完全二叉树构建成大顶堆，交换堆顶和堆尾，取出堆尾。这样每次都是取出当前堆中最大的数据，添加到已排序序列中，直到堆中的数据全部被取出。

14. 循环进行 n 轮堆排序之后，列表排序完成。排序结果如下图。

三、Python实现堆排序

# coding=utf-8
def heap_sort(array):
    first = len(array) // 2 - 1
    for start in range(first, -1, -1):
        # 从下到上，从右到左对每个非叶节点进行调整，循环构建成大顶堆
        big_heap(array, start, len(array) - 1)
    for end in range(len(array) - 1, 0, -1):
        # 交换堆顶和堆尾的数据
        array[0], array[end] = array[end], array[0]
        # 重新调整完全二叉树，构造成大顶堆
        big_heap(array, 0, end - 1)
    return array
 
 
def big_heap(array, start, end):
    root = start
    # 左孩子的索引
    child = root * 2 + 1
    while child <= end:
        # 节点有右子节点，并且右子节点的值大于左子节点，则将child变为右子节点的索引
        if child + 1 <= end and array[child] < array[child + 1]:
            child += 1
        if array[root] < array[child]:
            # 交换节点与子节点中较大者的值
            array[root], array[child] = array[child], array[root]
            # 交换值后，如果存在孙节点，则将root设置为子节点，继续与孙节点进行比较
            root = child
            child = root * 2 + 1
        else:
            break
 
 
if __name__ == '__main__':
    array = [10, 17, 50, 7, 30, 24, 27, 45, 15, 5, 36, 21]
    print(heap_sort(array))

运行结果：

[5, 7, 10, 15, 17, 21, 24, 27, 30, 36, 45, 50]

代码中，先实现一个big_heap(array, start, end)函数，用于比较节点与其子节点中的较大者，如果值小于子节点的值则进行交换。代码中不需要真正将数据都添加到完全二叉树中，而是根据待排序列表中的数据索引来得到节点与子节点的位置关系。完全二叉树中，节点的索引为i，则它的左子节点的索引为2*i+1，右子节点的索引为2*i+2，有n个节点的完全二叉树中，非叶子节点有n//2个，列表的索引从0开始，所以索引为0~n//2-1的数据为非叶子节点。

实现堆排序函数heap_sort(array)时，先调用big_heap(array, start, end)函数循环对非叶子节点进行调整，构造大顶堆，然后将堆顶和堆尾交换，将堆尾从堆中取出，添加到已排序序列中，完成一轮堆排序。然后循环构建大顶堆，每次将最大的元素取出，直到堆中的数据全部被取出。

四、堆排序的时间复杂度和稳定性

1. 时间复杂度

在堆排序中，构建一次大顶堆可以取出一个元素，完成一轮堆排序，一共需要进行n轮堆排序。每次构建大顶堆时，需要进行的比较和交换次数平均为logn(第一轮构建堆时步骤多，后面重建堆时步骤会少很多)。时间复杂度为 T(n)=nlogn ，再乘每次操作的步骤数(常数，不影响大O记法)，所以堆排序的时间复杂度为 O(nlogn) 。

2. 稳定性

在堆排序中，会交换节点与子节点，如果有相等的数据，可能会改变相等数据的相对次序。所以堆排序是一种不稳定的排序算法。