python 高斯模糊 python实现高斯模糊及原理详解
kelly学挖掘 人气:5高斯模糊是一种常见的模糊技术,相关知识点有:高斯函数、二维卷积。

(一)一维高斯分布函数
一维(连续变量)高斯函数形式如下,高斯函数又称“正态分布函数”:
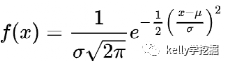
μ是分布函数的均值(或者期望),sigma是标准差。
一维高斯分布函数的图形:
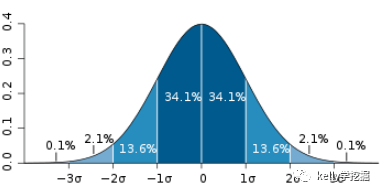
从图可知,以x=0为中心,x取值距离中心越近,概率密度函数值越大,距离中心越远,密度函数值越小。
(二)二维高斯分布函数
二维高斯分布函数的形式:
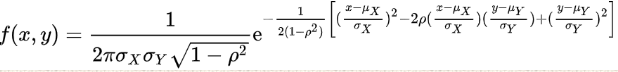
特别说明,当变量x和y相互独立时,则相关系数ρ=0,二维高斯分布函数可以简化为:
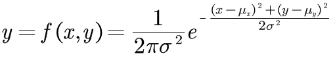
二维高斯分布函数的图形:
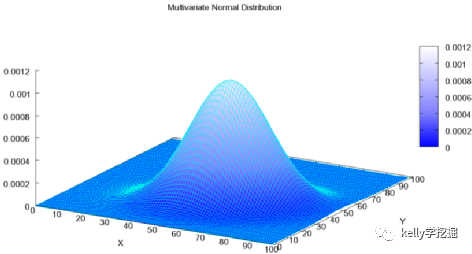
对于一维高斯分布,函数中心是平面上的一个点;而对于二维高斯分布,函数中心是一个三维立体空间上的一个点,即上图中山峰的最顶端处的点。
(三)高斯模糊
高斯模糊本质上一种数据平滑技术,可以用于一维、二维甚至多维空间。数据经高斯模糊处理之后,数据会趋向于周边邻近的其他数据,导致各个数据“趋同”。
在图像领域,各个位置的像素值使用“周边邻居像素点加权平均”重新赋值。对于每个像素点,由于计算时均以当前像素点为中心,所以均值μ=0。使用时有2个超参数需要设置:高斯核大小和高斯函数标准差σ。高斯核大小表示“影响当前点的最大邻域范围”,而标准差表示“邻域中的其他像素点对当前点的影响力”。
从下而上观察下图各个函数图像,各个函数的均值相同,而方差逐步减小。
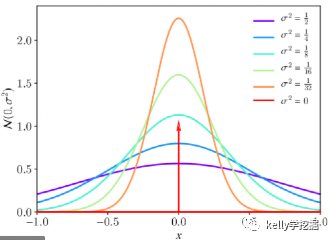
方差衡量数据的分散程度,方差越大,数据越分散,图形就越扁平,数据的集中趋势越弱,应用到高斯模糊中方差越大图形越模糊。
高斯模糊涉及到2个关键技术点:
(1)如何计算高斯卷积核
3×3大小的高斯卷积核的计算示意图
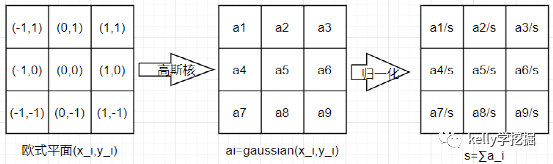
直接计算二维高斯函数值后,卷积核的各个位置取值(截图自pycharm的debug):
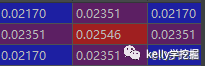
卷积核归一化后的各个位置取值(截图自pycharm的debug):
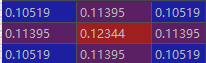
高斯卷积核的python代码:
def gaussian_kernel(self): kernel = np.zeros(shape=(self.kernel_size, self.kernel_size), dtype=np.float) radius = self.kernel_size//2 for y in range(-radius, radius + 1): # [-r, r] for x in range(-radius, radius + 1): # 二维高斯函数 v = 1.0 / (2 * np.pi * self.sigma ** 2) * np.exp(-1.0 / (2 * self.sigma ** 2) * (x ** 2 + y ** 2)) kernel[y + radius, x + radius] = v # 高斯函数的x和y值 vs 高斯核的下标值 kernel2 = kernel / np.sum(kernel) return kernel2
(2)如何在二维图像上进行卷积
对于二维矩阵,卷积时卷积核从左向右、从上而下的滑动,对应位置求加权和。一般图像是RGB三通道,需要逐个通道卷积,每个通道是一个二维矩阵。灰度图只有一个通道,直接卷积即可。
自行实现的二维离散卷积的python代码:
def my_conv2d(inputs: np.ndarray, kernel: np.ndarray):
# 计算需要填充的行列数目,这里假定mode为“same”
# 一般卷积核的hw都是奇数,这里实现方式也是基于奇数尺寸的卷积核
h, w = inputs.shape
kernel = kernel[::-1, ...][..., ::-1] # 卷积的定义,必须旋转180度
h1, w1 = kernel.shape
h_pad = (h1 - 1) // 2
w_pad = (w1 - 1) // 2
inputs = np.pad(inputs, pad_width=[(h_pad, h_pad), (w_pad, w_pad)], mode="constant", constant_values=0)
outputs = np.zeros(shape=(h, w))
for i in range(h): # 行号
for j in range(w): # 列号
outputs[i, j] = np.sum(np.multiply(inputs[i: i + h1, j: j + w1], kernel))
return outputs
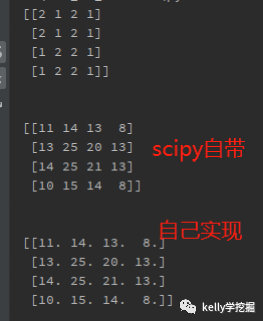
scipy中已经提供二维卷积函数scipy.signal.convolve2d,可以直接调用,下图是和自行实现的对比效果。
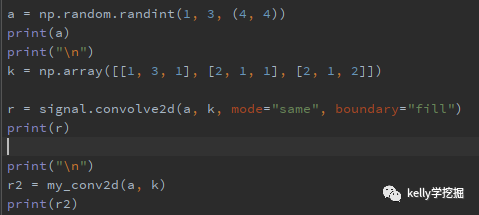
运行之后结果一致,验证自行实现的二维卷积正确。
补充:scipy.signal.convolve2d的参数说明
in1:输入矩阵
in2:卷积核
mode:指示输出矩阵的尺寸,full代表完全离散线性卷积, valid代表输出尺寸等于输入尺寸-卷积核+1, same代表输出尺寸与输入尺寸一致。
boundary:需要填充时边界填充方式,fill代表使用常量值填充, wrap代表循环方式填充, symm代表以四周边为对称轴对称填充。
fillvalue:常量填充时的填充值
(四)完整代码和运行效果
完整的python代码
class GaussianBlur(object):
def __init__(self, kernel_size=3, sigma=1.5):
self.kernel_size = kernel_size
self.sigma = sigma
self.kernel = self.gaussian_kernel()
def gaussian_kernel(self):
kernel = np.zeros(shape=(self.kernel_size, self.kernel_size), dtype=np.float)
radius = self.kernel_size//2
for y in range(-radius, radius + 1): # [-r, r]
for x in range(-radius, radius + 1):
# 二维高斯函数
v = 1.0 / (2 * np.pi * self.sigma ** 2) * np.exp(-1.0 / (2 * self.sigma ** 2) * (x ** 2 + y ** 2))
kernel[y + radius, x + radius] = v # 高斯函数的x和y值 vs 高斯核的下标值
kernel2 = kernel / np.sum(kernel)
return kernel2
def filter(self, img: Image.Image):
img_arr = np.array(img)
if len(img_arr.shape) == 2:
new_arr = signal.convolve2d(img_arr, self.kernel, mode="same", boundary="symm")
else:
h, w, c = img_arr.shape
new_arr = np.zeros(shape=(h, w, c), dtype=np.float)
for i in range(c):
new_arr[..., i] = signal.convolve2d(img_arr[..., i], self.kernel, mode="same", boundary="symm")
new_arr = np.array(new_arr, dtype=np.uint8)
return Image.fromarray(new_arr)
def main():
img = Image.open("Jeep-cd.jpg").convert("RGB")
img2 = GaussianBlur(sigma=2.5).filter(img)
plt.subplot(1, 2, 1)
plt.imshow(img)
plt.subplot(1, 2, 2)
plt.imshow(img2)
# dpi参数维持图片的清晰度
plt.savefig("gaussian.jpg", dpi=500)
plt.show()
pass
代码运行效果,发现经高斯模糊处理之后,图片发生明显模糊。


加载全部内容