写给程序员的机器学习入门 (三) - 线性模型,激活函数与多层线性模型
q303248153 人气:0生物神经元与人工神经元
在了解神经元网络之前,我们先简单的看看生物学上的神经元是什么样子的,下图摘自维基百科:
(因为我不是专家,这里的解释只用于理解人工神经元模拟了生物神经元的什么地方,不一定完全准确)
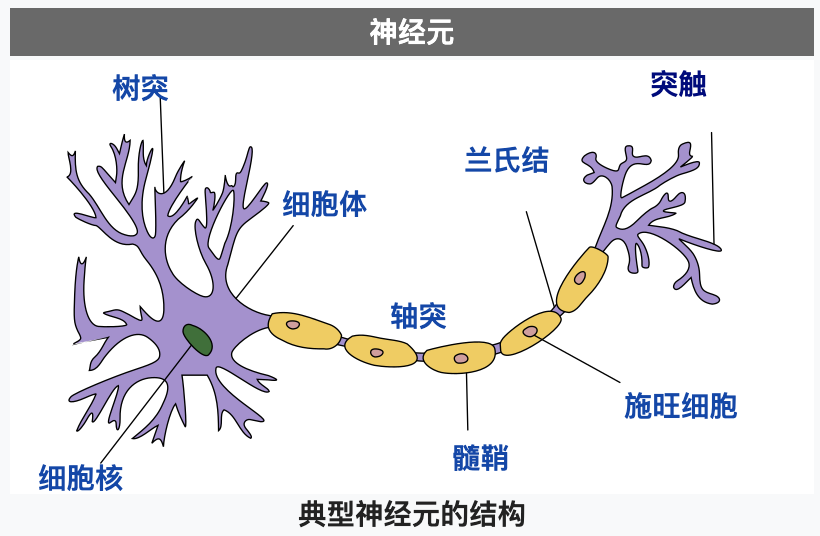
神经元主要由细胞体和细胞突组成,而细胞突分为树突 (Dendrites) 和轴突 (Axon),树突负责接收其他神经元输入的电流,而轴突负责把电流输出给其他神经元。一个神经元可以通过树突从多个神经元接收电流,如果电流没有达到某个阈值则神经元不会把电流输出,如果电流达到了某个阈值则神经元会通过轴突的突触把电流输出给其他神经元,这样的规则被称为全有全无律。输入电流达到阈值以后输出电流的状态又称为到达动作电位,动作电位会持续 1 ~ 2 毫秒,之后会进入约 0.5 毫秒的绝对不应期,无论输入多大的电流都不会输出,然后再进入约 3.5 毫秒的相对不应期,需要电流达到更大的阈值才会输出,最后返回静息电位。神经元之间连接起来的网络称为神经元网络,人的大脑中大约有 860 亿个神经元,因为 860 亿个神经元可以同时工作,所以目前的计算机无法模拟这种工作方式 (除非开发专用的芯片),只能模拟一部分的工作方式和使用更小规模的网络。
计算机模拟神经元网络使用的是人工神经元,单个人工神经元可以用以下公式表达:
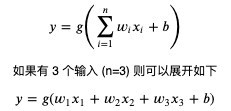
其中 n 代表输入的个数,你可以把 n 看作这个神经元拥有的树突个数,x 看作每个树突输入电流的值;而 w (weight) 代表各个输入的权重,也就是各个树突对电流大小的调整;而 b (bias) 用于调整各个输入乘权重相加后的值,使得这个值可以配合某个阈值工作;而 g 则是激活函数,用于判断值是否达到阈值并输出和输出多少,通常会使用非线性函数;而 y 则是输出的值,可以把它看作轴突输出的电流,连接这个 y 到其他神经元就可以组建神经元网络。
我们在前两篇看到的其实就是只有一个输入并且没有激活函数的单个人工神经元,把同样的输入传给多个神经元 (第一层),然后再传给其他神经元 (第二层),然后再传给其他神经元 (第三层) 就可以组建人工神经元网络了,同一层的神经元个数越多,神经元的层数越多,网络就越强大,但需要更多的运算时间并且更有可能发生第一篇文章讲过的过拟合 (Overfitting) 现象。
下图是人工神经元网络的例子,有 3 输入 1 个输出,经过 3 层处理,第 1 层和第 2 层各有两个神经元对应隐藏值 (中间值),第 3 层有一个神经元对应输出值:
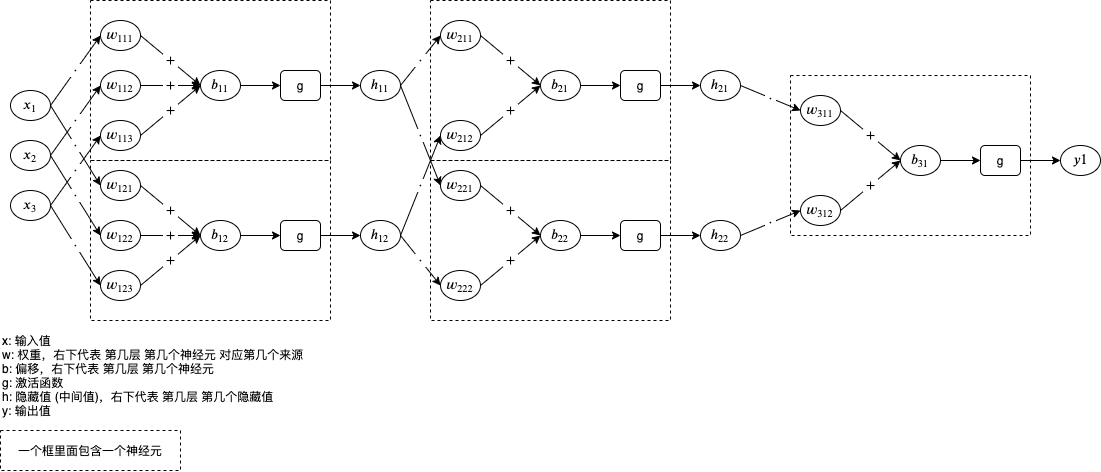
神经元中包含的 w 和 b 就是我们需要通过机器学习调整的参数值。
如果你觉得图片有点难以理解,可以看转换后的代码:
h11 = g(x1 * w111 + x2 * w112 + x3 * w113 + b11)
h12 = g(x1 * w121 + x2 * w122 + x3 * w123 + b12)
h21 = g(h11 * w211 + h12 * w212 + b21)
h22 = g(h11 * w221 + h12 * w222 + b22)
y = g(h21 * w311 + h22 * w312 + b31)
很多痴迷人工神经元网络的学者声称人工神经元网络可以模拟人脑的工作方式,做到某些领域上超过人脑的判断,但实际上这还有很大的争议,我们可以看到人工神经元的连接方式只会按固定的模式,判断是否达到阈值并输出的逻辑也无法做到和生物神经元一样(目前还没有解明),并且也没有生物神经元的不应期,所以也有学者声称人工神经元不过只是做了复杂的数学运算来模拟逻辑判断,需要根据不同的场景切换不同的计算方法,使用这种方式并不能达到人脑的水平。
单层线性模型
在前一篇文章我们已经稍微了解过机器学习框架 pytorch,现在我们来看看怎么使用 pytorch 封装的线性模型,以下代码运行在 python 的 REPL 中:
# 导入 pytorch 类库
>>> import torch
# 创建 pytorch 封装的线性模型,设置输入有 3 个输出有 1 个
>>> model = torch.nn.Linear(in_features=3, out_features=1)
# 查看线性模型内部包含的参数列表
# 这里一共包含两个参数,第一个参数是 1 行 3 列的矩阵分别表示 3 个输入对应的 w 值 (权重),第二个参数表示 b 值 (偏移)
# 初始值会随机生成 (使用 kaiming_uniform 生成正态分布)
>>> list(model.parameters())
[Parameter containing:
tensor([[0.0599, 0.1324, 0.0099]], requires_grad=True), Parameter containing:
tensor([-0.2772], requires_grad=True)]
# 定义输入和输出
>>> x = torch.tensor([1, 2, 3], dtype=torch.float)
>>> y = torch.tensor([6], dtype=torch.float)
# 把输入传给模型
>>> p = model(x)
# 查看预测输出值
# 1 * 0.0599 + 2 * 0.1324 + 3 * 0.0099 - 0.2772 = 0.0772
>>> p
tensor([0.0772], grad_fn=<AddBackward0>)
# 计算误差并自动微分
>>> l = (p - y).abs()
>>> l
tensor([5.9228], grad_fn=<AbsBackward>)
>>> l.backward()
# 查看各个参数对应的导函数值
>>> list(model.parameters())[0].grad
tensor([[-1., -2., -3.]])
>>> list(model.parameters())[1].grad
tensor([-1.])
以上可以看作 1 层 1 个神经元,很好理解吧?我们来看看 1 层 2 个神经元:
# 导入 pytorch 类库
>>> import torch
# 创建 pytorch 封装的线性模型,设置输入有 3 个输出有 2 个
>>> model = torch.nn.Linear(in_features=3, out_features=2)
# 查看线性模型内部包含的参数列表
# 这里一共包含两个参数
# 第一个参数是 2 行 3 列的矩阵分别表示 2 个输出和 3 个输入对应的 w 值 (权重)
# 第二个参数表示 2 个输出对应的 b 值 (偏移)
>>> list(model.parameters())
[Parameter containing:
tensor([[0.1393, 0.5165, 0.2910],
[0.2276, 0.1579, 0.1958]], requires_grad=True), Parameter containing:
tensor([0.2566, 0.1701], requires_grad=True)]
# 定义输入和输出
>>> x = torch.tensor([1, 2, 3], dtype=torch.float)
>>> y = torch.tensor([6, -6], dtype=torch.float)
# 把输入传给模型
>>> p = model(x)
# 查看预测输出值
# 1 * 0.1393 + 2 * 0.5165 + 3 * 0.2910 + 0.2566 = 2.3019
# 1 * 0.2276 + 2 * 0.1579 + 3 * 0.1958 + 0.1701 = 1.3009
>>> p
tensor([2.3019, 1.3009], grad_fn=<AddBackward0>)
# 计算误差并自动微分
# (abs(2.3019 - 6) + abs(1.3009 - -6)) / 2 = 5.4995
>>> l = (p - y).abs().mean()
>>> l
tensor(5.4995, grad_fn=<MeanBackward0>)
>>> l.backward()
# 查看各个参数对应的导函数值
# 因为误差取了 2 个值的平均,所以求导函数值的时候会除以 2
>>> list(model.parameters())[0].grad
tensor([[-0.5000, -1.0000, -1.5000],
[ 0.5000, 1.0000, 1.5000]])
>>> list(model.parameters())[1].grad
tensor([-0.5000, 0.5000])
现在我们来试试用线性模型来学习符合 x_1 * 1 + x_2 * 2 + x_3 * 3 + 8 = y 的数据,输入和输出会使用矩阵定义:
# 引用 pytorch
import torch
# 给随机数生成器分配一个初始值,使得每次运行都可以生成相同的随机数
# 这是为了让训练过程可重现,你也可以选择不这样做
torch.random.manual_seed(0)
# 创建线性模型,设置有 3 个输入 1 个输出
model = torch.nn.Linear(in_features=3, out_features=1)
# 创建损失计算器
loss_function = torch.nn.MSELoss()
# 创建参数调整器
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
# 随机生成原始数据集,一共 20 组数据,每条数据有 3 个输入
dataset_x = torch.randn((20, 3))
dataset_y = dataset_x.mm(torch.tensor([[1], [2], [3]], dtype=torch.float)) + 8
print(f"dataset_x: {dataset_x}")
print(f"dataset_y: {dataset_y}")
# 切分训练集 (12 组),验证集 (4 组) 和测试集 (4 组)
random_indices = torch.randperm(dataset_x.shape[0])
traning_indices = random_indices[:int(len(random_indices)*0.6)]
validating_indices = random_indices[int(len(random_indices)*0.6):int(len(random_indices)*0.8):]
testing_indices = random_indices[int(len(random_indices)*0.8):]
traning_set_x = dataset_x[traning_indices]
traning_set_y = dataset_y[traning_indices]
validating_set_x = dataset_x[validating_indices]
validating_set_y = dataset_y[validating_indices]
testing_set_x = dataset_x[testing_indices]
testing_set_y = dataset_y[testing_indices]
# 开始训练过程
for epoch in range(1, 10000):
print(f"epoch: {epoch}")
# 根据训练集训练并修改参数
# 切换模型到训练模式,将会启用自动微分,批次正规化 (BatchNorm) 与 Dropout
model.train()
# 计算预测值
# 20 行 3 列的矩阵乘以 3 行 1 列的矩阵 (由 weight 转置得到) 等于 20 行 1 列的矩阵
predicted = model(traning_set_x)
# 计算损失
loss = loss_function(predicted, traning_set_y)
# 打印除错信息
print(f"loss: {loss}, weight: {model.weight}, bias: {model.bias}")
# 从损失自动微分求导函数值
loss.backward()
# 使用参数调整器调整参数
optimizer.step()
# 清空导函数值
optimizer.zero_grad()
# 检查验证集
# 切换模型到验证模式,将会禁用自动微分,批次正规化 (BatchNorm) 与 Dropout
model.eval()
predicted = model(validating_set_x)
validating_accuracy = 1 - ((validating_set_y - predicted).abs() / validating_set_y).abs().mean()
print(f"validating x: {validating_set_x}, y: {validating_set_y}, predicted: {predicted}")
# 如果验证集正确率大于 99 %,则停止训练
print(f"validating accuracy: {validating_accuracy}")
if validating_accuracy > 0.99:
break
# 检查测试集
predicted = model(testing_set_x)
testing_accuracy = 1 - ((testing_set_y - predicted).abs() / testing_set_y).abs().mean()
print(f"testing x: {testing_set_x}, y: {testing_set_y}, predicted: {predicted}")
print(f"testing accuracy: {testing_accuracy}")
输出结果如下:
dataset_x: tensor([[ 0.8487, 0.6920, -0.3160],
[-2.1152, -0.3561, 0.4372],
[ 0.4913, -0.2041, 0.1198],
[ 1.2377, 1.1168, -0.2473],
[-1.0438, -1.3453, 0.7854],
[ 0.9928, 0.5988, -1.5551],
[-0.3414, 1.8530, 0.4681],
[-0.1577, 1.4437, 0.2660],
[ 1.3894, 1.5863, 0.9463],
[-0.8437, 0.9318, 1.2590],
[ 2.0050, 0.0537, 0.4397],
[ 0.1124, 0.6408, 0.4412],
[-0.2159, -0.7425, 0.5627],
[ 0.2596, 0.5229, 2.3022],
[-1.4689, -1.5867, -0.5692],
[ 0.9200, 1.1108, 1.2899],
[-1.4782, 2.5672, -0.4731],
[ 0.3356, -1.6293, -0.5497],
[-0.4798, -0.4997, -1.0670],
[ 1.1149, -0.1407, 0.8058]])
dataset_y: tensor([[ 9.2847],
[ 6.4842],
[ 8.4426],
[10.7294],
[ 6.6217],
[ 5.5252],
[12.7689],
[11.5278],
[15.4009],
[12.7970],
[11.4315],
[10.7175],
[ 7.9872],
[16.2120],
[ 1.6500],
[15.0112],
[10.2369],
[ 3.4277],
[ 3.3199],
[11.2509]])
epoch: 1
loss: 142.77590942382812, weight: Parameter containing:
tensor([[-0.0043, 0.3097, -0.4752]], requires_grad=True), bias: Parameter containing:
tensor([-0.4249], requires_grad=True)
validating x: tensor([[-0.4798, -0.4997, -1.0670],
[ 0.8487, 0.6920, -0.3160],
[ 0.1124, 0.6408, 0.4412],
[-1.0438, -1.3453, 0.7854]]), y: tensor([[ 3.3199],
[ 9.2847],
[10.7175],
[ 6.6217]]), predicted: tensor([[-0.1385],
[ 0.3020],
[-0.0126],
[-1.1801]], grad_fn=<AddmmBackward>)
validating accuracy: -0.04714548587799072
epoch: 2
loss: 131.40403747558594, weight: Parameter containing:
tensor([[ 0.0675, 0.4937, -0.3163]], requires_grad=True), bias: Parameter containing:
tensor([-0.1970], requires_grad=True)
validating x: tensor([[-0.4798, -0.4997, -1.0670],
[ 0.8487, 0.6920, -0.3160],
[ 0.1124, 0.6408, 0.4412],
[-1.0438, -1.3453, 0.7854]]), y: tensor([[ 3.3199],
[ 9.2847],
[10.7175],
[ 6.6217]]), predicted: tensor([[-0.2023],
[ 0.6518],
[ 0.3935],
[-1.1479]], grad_fn=<AddmmBackward>)
validating accuracy: -0.03184401988983154
epoch: 3
loss: 120.98343658447266, weight: Parameter containing:
tensor([[ 0.1357, 0.6687, -0.1639]], requires_grad=True), bias: Parameter containing:
tensor([0.0221], requires_grad=True)
validating x: tensor([[-0.4798, -0.4997, -1.0670],
[ 0.8487, 0.6920, -0.3160],
[ 0.1124, 0.6408, 0.4412],
[-1.0438, -1.3453, 0.7854]]), y: tensor([[ 3.3199],
[ 9.2847],
[10.7175],
[ 6.6217]]), predicted: tensor([[-0.2622],
[ 0.9860],
[ 0.7824],
[-1.1138]], grad_fn=<AddmmBackward>)
validating accuracy: -0.016991496086120605
省略途中输出
epoch: 637
loss: 0.001102567883208394, weight: Parameter containing:
tensor([[1.0044, 2.0283, 3.0183]], requires_grad=True), bias: Parameter containing:
tensor([7.9550], requires_grad=True)
validating x: tensor([[-0.4798, -0.4997, -1.0670],
[ 0.8487, 0.6920, -0.3160],
[ 0.1124, 0.6408, 0.4412],
[-1.0438, -1.3453, 0.7854]]), y: tensor([[ 3.3199],
[ 9.2847],
[10.7175],
[ 6.6217]]), predicted: tensor([[ 3.2395],
[ 9.2574],
[10.6993],
[ 6.5488]], grad_fn=<AddmmBackward>)
validating accuracy: 0.9900396466255188
testing x: tensor([[-0.3414, 1.8530, 0.4681],
[-1.4689, -1.5867, -0.5692],
[ 1.1149, -0.1407, 0.8058],
[ 0.3356, -1.6293, -0.5497]]), y: tensor([[12.7689],
[ 1.6500],
[11.2509],
[ 3.4277]]), predicted: tensor([[12.7834],
[ 1.5438],
[11.2217],
[ 3.3285]], grad_fn=<AddmmBackward>)
testing accuracy: 0.9757462739944458
可以看到最终 weight 接近 1, 2, 3,bias 接近 8。和前一篇文章最后的例子比较还可以发现代码除了定义模型的部分以外几乎一模一样 (后面的代码基本上都是相同的结构,这个系列是先学套路在学细节
加载全部内容
- 猜你喜欢
- 用户评论