C#大牛生小牛的问题 C#算法之大牛生小牛的问题高效解决办法

时间:2021-03-22 Robin 人气:0

想了解C#算法之大牛生小牛的问题高效解决办法的相关内容吗，Robin在本文为您仔细讲解C#大牛生小牛的问题的相关知识和一些Code实例，欢迎阅读和指正，我们先划重点：C#,算法,大牛生小牛,循环，下面大家一起来学习吧。

问题：
　　一只刚出生的小牛，4年后生一只小牛，以后每年生一只。现有一只刚出生的小牛，问20年后共有牛多少只？
思路：
　　这种子生孙，孙生子，子子孙孙的问题，循环里面还有循环的嵌套循环，一看就知道是第归问题。
于是乎,第一个版本出现：

public long Compute1(uint years)
{
  //初始化为1头牛
  long count = 1;
  if (years <= 3)
  {
    return count;
  }
  int i = 4;
  while (i <= years)
  {
    int subYears = i - 3;
    count += Compute1((uint)(subYears));
    i++;
  }
  return (long)count;
}

　　可是这种循环在循环的做法可要把cpu老兄累坏了，你不信输入一个100年测试一下上面的方法，我等了半天，都没结果，改进一下吧，老牛（牛魔王）和小牛（红孩儿，奶奶的串种了），具有相同的生育能力，他们的生育曲线是一样的，所以小牛可以复用老牛的生育经验亚，这样就解决了重复计算一只牛第n年的时候一共生多少只的问题了，当年龄比较大的时候，明显大大降低cpu的运算次数，下面是基于这种思路的算法

Hashtable table = new Hashtable();
public long Compute(uint years)
{
  //初始化为1头牛
  long count = 1;
  if (years <= 3)
  {
    return count;
  }
  int i = 4;
  while (i <= years)
  {
    int subYears = i - 3;
    if (table.ContainsKey(subYears))
    {
      count = (long)table[subYears];
    }
    else
    {
      count += Compute((uint)(subYears));
    }
    if (!table.ContainsKey(subYears))
    {
      table.Add(subYears, count);
    }
    i++;
  }
  return (long)count;
}

用测试程序测试一下上面的推论吧，结果如下:

1）当输入years比较小的时候，第一种方法耗时短，但两者的时间基本在一个数量级上
2）当输入years比较大的时候，比如40以上的，第二种算法比第一种性能比在100以上，而且输入years越高，性能比越悬殊。

测试结果截图：

20年

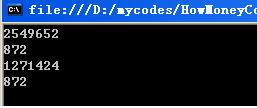
50年

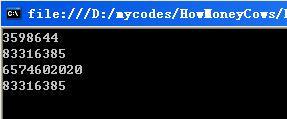
源程序以及测试程序：http://xiazai.jb51.net/201606/yuanma/HowMoneyCows(jb51.net).rar

以上就是本文的全部内容，希望能给大家一个参考，也希望大家多多支持。

加载全部内容