关于 JavaScript 的 精度丢失 与 近似舍入
小蒋不素小蒋 人气:1
# 一、背景
---
最近做 dashborad 图表时,涉及计算小数且四舍五入精确到 N 位。后发现 js 算出来的结果跟我预想的不一样,看来这里面并不简单……
# 二、JS 与 精度
---
### 1、精度处理
首先明确两点:
- 1、小数才会涉及精度的概念
- 2、小数的(存储和)**运算**涉及 JS 的`精度处理`
在现实中,我们运算小数,不会出现任何问题。但是 JS (编程语言)里,却不是这样。
### 2、精度丢失
例如,在 JS 里执行:
```
0.1 + 0.2
0.30000000000000004
0.3 - 0.1
0.19999999999999998
0.1 * 0.1
0.010000000000000002
0.3 / 0.1
2.9999999999999996
```
可以看出,JS 运算小数的结果,并不是我们预想的那样。这就是`精度丢失`的问题。
##### (1)问:精度丢失会引发什么问题?
答:
- 1、让判断等于(`===`)的逻辑出错。比如让 `0.1 + 0.2 === 0.3` 为 `false`
- 2、让本来可以预想到的结果精度变的特别大,小数点后位数特别长。比如若要前端显示,会特别难看。
##### (2)问:为什么会出现精度丢失?
答:这跟**浮点数在计算机内部(用二进制存储)的表示方法**有关。
JS 采用 `IEEE 754` 标准的 64 位双精度浮点数表示法,这个标准是20世纪80年代以来最广泛使用的浮点数运算标准,为许多CPU与浮点运算器所采用,也被很多语言如 java、python 采用。
这个标准,会让绝大部分的十进制小数都不能用二进制浮点数来精确表示(事实上,根本没有什么标准可以精确表示浮点数)。一般情况下,你输入的十进制小数仅由实际存储在计算机中的**近似的二进制浮点数表示**。
然而,许多语言在处理的时候,在一定误差范围内(通常极小)会将结果修正为正确的目标数字,**而不是像 JS 一样将存在误差的真实结果转换成最接近的小数输出。**
> 具体原理可以看[《浮点数的二进制表示 —— 阮一峰》](https://www.ruanyifeng.com/blog/2010/06/ieee_floating-point_representation.html),这里不赘述了。
##### (3)问:怎么避免精度丢失?
方法一:**中途变成整数来计算**
比如我们要计算 0.1 + 0.2,就先把数字全部乘以 10 使之变成整数,再相加,最后把结果除以 10。
> 因为**整数是不会出现精度丢失**的问题。(况且整数根本就没有精度)
> 其实很多第三方的库,原理也是用的这个。
方法二:**使用第三方库** - Math.js - decimal.js - big.js - bignumber.js
方法三:**使用 toFixed() 函数**(推荐) ``` console.log(parseFloat((0.3 + 0.1).toFixed(1))) // 0.4 ``` 注意:`toFixed()` 最好跟 `parseFloat()` 搭配使用。因为 toFixed **返回的是字符串**。 问:`toFixed()` 为什么要返回字符串,而不是小数?【重点】 答:因为 JavaScript 的数据类型,关于数字的只有 `number` 类型(不像 C 语言 or 数据库等还分 int、float、double),而对于 number 类型来说, **会忽略前置0和小数点后的后置0**(比如 001 是 1; 1.1000 是 1.1)。 > 在下面还会继续介绍 `toFixed()` 的关于舍入的特性。 # 三、JS 与 近似计算方法 --- 在上面提到的: - 精度计算 - 精度丢失 都会有可能让精度发生变化(即小数点后位数变化)。如果我们需要统一精度,那就需要用到`近似(计算)方法`。 ### 1、四舍五入 ##### (1)规则 四舍五入是最常见的近似计算方法,具体规则顾名思义,不赘述了。 ##### (2)Math.round() 给定数字的值四舍五入到最接近的**整数**。 ``` Math.Round(2.4) // 2 Math.Round(2.5) // 3 ``` ##### (3)_.round() —— lodash 给定数字的值四舍五入到最接近的**数**(可以是小数)。 lodash 的这个方法,我看了源码,底层也是调用的 Math.round(),只是加了一些额外功能,比如第二个参数,可以指定四舍五入的精度。 ``` const _ = require('lodash'); _.round(1.04, 1) //1 _.round(1.05, 1) //1.1 ``` ##### (4)四舍五入真的公平吗?【重点】 因为自己很小的时候就在学校学到了四舍五入,一直想当然的认为四舍五入是公平的,等到现在细想的时候,才发现,真的**不公平**。 例如,想象一个场景,你的余额宝,每天会自动结算利息,但是可能(按照利息规则)算出来的值的小数有很多位,假设支付宝只支持到角,那么支付宝系统帮你记账的时候,肯定会给你近似计算,如果他用的是四舍五入的方法: ``` const _ = require('lodash'); console.log(_.round(1.01, 1)) //1 (我亏了0.01) console.log(_.round(1.02, 1)) //1 (我亏了0.02) console.log(_.round(1.03, 1)) //1 (我亏了0.03) console.log(_.round(1.04, 1)) //1 (我亏了0.04) console.log(_.round(1.05, 1)) //1.1 (我赚了了0.05) console.log(_.round(1.06, 1)) //1.1 (我赚了0.04) console.log(_.round(1.07, 1)) //1.1 (我赚了0.03) console.log(_.round(1.08, 1)) //1.1 (我赚了0.02) console.log(_.round(1.09, 1)) //1.1 (我赚了0.01) ``` 首先,1 块钱整和 2 块钱整可以不用考虑,其次,如果假设 1.01 到 1.09 这 9 个数出现的概率一致。那么最后支付宝肯定要**亏本**,因为 1.05 划分到 1.1 是不公平的。 也可以画一个**数轴**来体现: 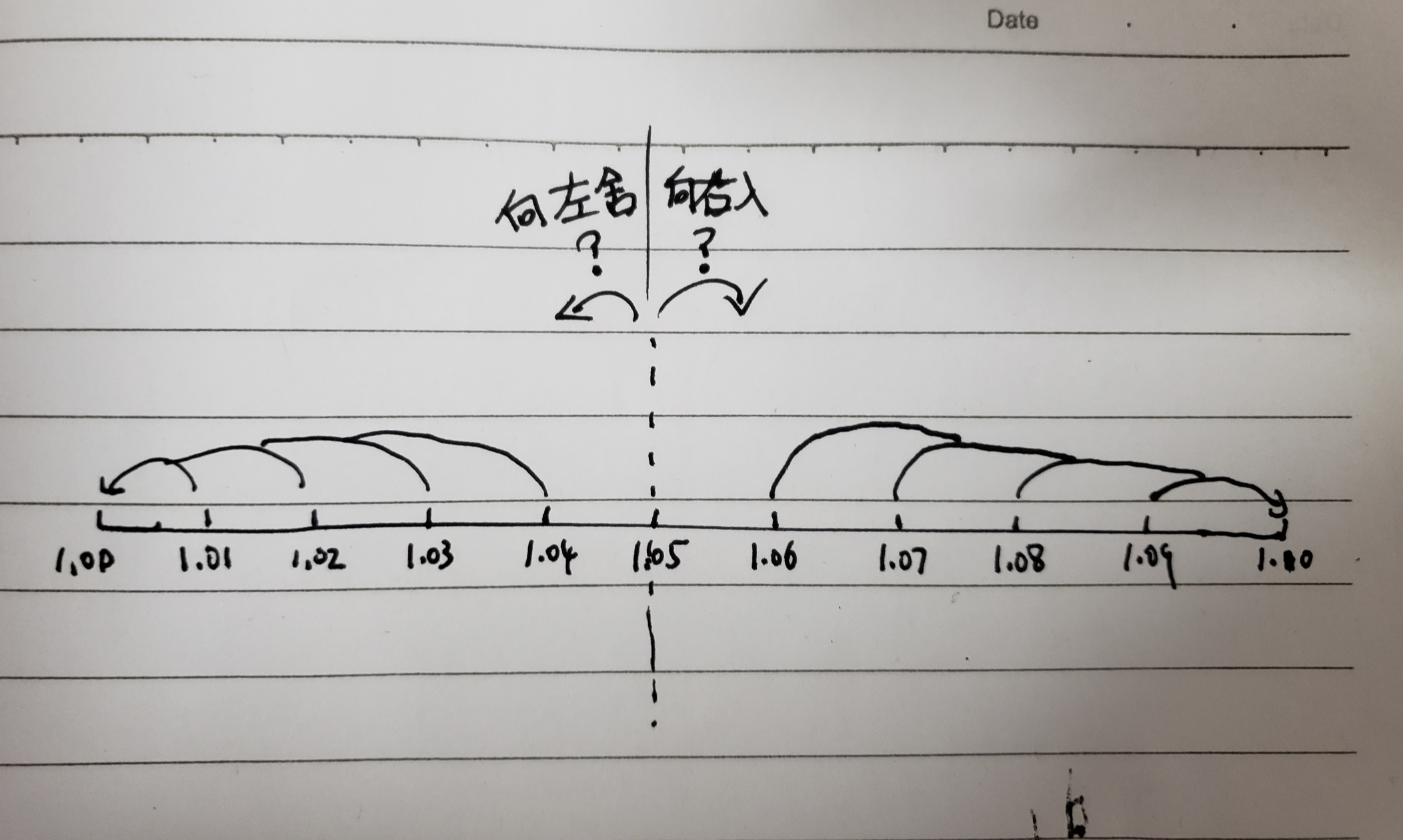 那么如何做到更公平的近似计算呢?可以用下面介绍的银行家舍入。 ### 2、银行家舍入 国际通行的是 `银行家舍入`(Banker's rounding)算法 。 是 IEEE 规定的舍入标准。因此所有符合 IEEE 标准的语言都应该是采用这一规则的。 ##### (1)规则 银行家舍入又称**四舍六入五取偶**(又称四舍六入五留双)法。 所以规则就是:**四舍六入五考虑,五后非空就进一,五后为空看奇偶,五前为偶应舍去,五前为奇要进一**。 关键就是“五后为空看奇偶”,因为如果是舍入位是5,无论是舍还是入都不公平,那就交给它前一位的奇偶性来判断,因为奇偶性分布概率是公平的。 > 当然只能说银行家舍入算法比四舍五入算法**更科学**,而不能说它就是绝对正确,而四舍五入就是错误的,因为这些结果都是基于统计数据产生的,前提就是这些数据摇符合随机性分布的要求。 ##### (2)使用 目前 JS 上原生不支持,如果想使用: - 1、自己实现 - 2、使用第三方 npm 包,如 [bankers-rounding](https://www.npmjs.com/package/bankers-rounding) ### 3、toFixed toFixed() **部分符合银行家舍入**的规则。 ##### (1)四舍六入 符合 ##### (2)五后非空就进一 符合 ##### (3)五后为空看奇偶,五前为偶应舍去,五前为奇要进一 部分符合 ``` // //toFixed结果 //银行家舍入结果 console.log(1.05.toFixed(1)) //1.1(+0.05) 1.0(-0.05) console.log(1.15.toFixed(1)) //1.1(-0.05) 1.2(+0.05) console.log(1.25.toFixed(1)) //1.3(+0.05) 1.2(-0.05) console.log(1.35.toFixed(1)) //1.4(+0.05) 1.4(+0.05) console.log(1.45.toFixed(1)) //1.4(-0.05) 1.4(-0.05) console.log(1.55.toFixed(1)) //1.6(+0.05) 1.6(+0.05) console.log(1.65.toFixed(1)) //1.6(-0.05) 1.6(-0.05) console.log(1.75.toFixed(1)) //1.8(+0.05) 1.8(+0.05) console.log(1.85.toFixed(1)) //1.9(+0.05) 1.8(-0.05) console.log(1.95.toFixed(1)) //1.9(-0.05) 2.0(+0.05) // //总计(+0.1) //总计(0) ``` 可以看出 toFixed 肯定是不遵守四舍五入的,但是也跟银行家舍入算法有出入。(具体为什么是这样的计算方法,鄙人并不是弄清楚,待写) ### 4、其他 近似计算 函数 - Math.ceil():向上舍入(取整) - Math.floor():向下舍入(取整) - 等等……
方法二:**使用第三方库** - Math.js - decimal.js - big.js - bignumber.js
方法三:**使用 toFixed() 函数**(推荐) ``` console.log(parseFloat((0.3 + 0.1).toFixed(1))) // 0.4 ``` 注意:`toFixed()` 最好跟 `parseFloat()` 搭配使用。因为 toFixed **返回的是字符串**。 问:`toFixed()` 为什么要返回字符串,而不是小数?【重点】 答:因为 JavaScript 的数据类型,关于数字的只有 `number` 类型(不像 C 语言 or 数据库等还分 int、float、double),而对于 number 类型来说, **会忽略前置0和小数点后的后置0**(比如 001 是 1; 1.1000 是 1.1)。 > 在下面还会继续介绍 `toFixed()` 的关于舍入的特性。 # 三、JS 与 近似计算方法 --- 在上面提到的: - 精度计算 - 精度丢失 都会有可能让精度发生变化(即小数点后位数变化)。如果我们需要统一精度,那就需要用到`近似(计算)方法`。 ### 1、四舍五入 ##### (1)规则 四舍五入是最常见的近似计算方法,具体规则顾名思义,不赘述了。 ##### (2)Math.round() 给定数字的值四舍五入到最接近的**整数**。 ``` Math.Round(2.4) // 2 Math.Round(2.5) // 3 ``` ##### (3)_.round() —— lodash 给定数字的值四舍五入到最接近的**数**(可以是小数)。 lodash 的这个方法,我看了源码,底层也是调用的 Math.round(),只是加了一些额外功能,比如第二个参数,可以指定四舍五入的精度。 ``` const _ = require('lodash'); _.round(1.04, 1) //1 _.round(1.05, 1) //1.1 ``` ##### (4)四舍五入真的公平吗?【重点】 因为自己很小的时候就在学校学到了四舍五入,一直想当然的认为四舍五入是公平的,等到现在细想的时候,才发现,真的**不公平**。 例如,想象一个场景,你的余额宝,每天会自动结算利息,但是可能(按照利息规则)算出来的值的小数有很多位,假设支付宝只支持到角,那么支付宝系统帮你记账的时候,肯定会给你近似计算,如果他用的是四舍五入的方法: ``` const _ = require('lodash'); console.log(_.round(1.01, 1)) //1 (我亏了0.01) console.log(_.round(1.02, 1)) //1 (我亏了0.02) console.log(_.round(1.03, 1)) //1 (我亏了0.03) console.log(_.round(1.04, 1)) //1 (我亏了0.04) console.log(_.round(1.05, 1)) //1.1 (我赚了了0.05) console.log(_.round(1.06, 1)) //1.1 (我赚了0.04) console.log(_.round(1.07, 1)) //1.1 (我赚了0.03) console.log(_.round(1.08, 1)) //1.1 (我赚了0.02) console.log(_.round(1.09, 1)) //1.1 (我赚了0.01) ``` 首先,1 块钱整和 2 块钱整可以不用考虑,其次,如果假设 1.01 到 1.09 这 9 个数出现的概率一致。那么最后支付宝肯定要**亏本**,因为 1.05 划分到 1.1 是不公平的。 也可以画一个**数轴**来体现:  那么如何做到更公平的近似计算呢?可以用下面介绍的银行家舍入。 ### 2、银行家舍入 国际通行的是 `银行家舍入`(Banker's rounding)算法 。 是 IEEE 规定的舍入标准。因此所有符合 IEEE 标准的语言都应该是采用这一规则的。 ##### (1)规则 银行家舍入又称**四舍六入五取偶**(又称四舍六入五留双)法。 所以规则就是:**四舍六入五考虑,五后非空就进一,五后为空看奇偶,五前为偶应舍去,五前为奇要进一**。 关键就是“五后为空看奇偶”,因为如果是舍入位是5,无论是舍还是入都不公平,那就交给它前一位的奇偶性来判断,因为奇偶性分布概率是公平的。 > 当然只能说银行家舍入算法比四舍五入算法**更科学**,而不能说它就是绝对正确,而四舍五入就是错误的,因为这些结果都是基于统计数据产生的,前提就是这些数据摇符合随机性分布的要求。 ##### (2)使用 目前 JS 上原生不支持,如果想使用: - 1、自己实现 - 2、使用第三方 npm 包,如 [bankers-rounding](https://www.npmjs.com/package/bankers-rounding) ### 3、toFixed toFixed() **部分符合银行家舍入**的规则。 ##### (1)四舍六入 符合 ##### (2)五后非空就进一 符合 ##### (3)五后为空看奇偶,五前为偶应舍去,五前为奇要进一 部分符合 ``` // //toFixed结果 //银行家舍入结果 console.log(1.05.toFixed(1)) //1.1(+0.05) 1.0(-0.05) console.log(1.15.toFixed(1)) //1.1(-0.05) 1.2(+0.05) console.log(1.25.toFixed(1)) //1.3(+0.05) 1.2(-0.05) console.log(1.35.toFixed(1)) //1.4(+0.05) 1.4(+0.05) console.log(1.45.toFixed(1)) //1.4(-0.05) 1.4(-0.05) console.log(1.55.toFixed(1)) //1.6(+0.05) 1.6(+0.05) console.log(1.65.toFixed(1)) //1.6(-0.05) 1.6(-0.05) console.log(1.75.toFixed(1)) //1.8(+0.05) 1.8(+0.05) console.log(1.85.toFixed(1)) //1.9(+0.05) 1.8(-0.05) console.log(1.95.toFixed(1)) //1.9(-0.05) 2.0(+0.05) // //总计(+0.1) //总计(0) ``` 可以看出 toFixed 肯定是不遵守四舍五入的,但是也跟银行家舍入算法有出入。(具体为什么是这样的计算方法,鄙人并不是弄清楚,待写) ### 4、其他 近似计算 函数 - Math.ceil():向上舍入(取整) - Math.floor():向下舍入(取整) - 等等……
加载全部内容