分布式系统的一致性算法

看到了自己项目中使用单个redis实例实现的分布式锁，因此就把redis相关的知识点，以及Redlock等记录了下来，就有了Redis基础这篇随笔。

在理解Redlock算法时，看到了很多关于分布式系统中的一致性算法的文章，于站在巨人的肩膀上，温故而知新，今天就来做些总结整理。

 

一：分布式系统和一致性问题

分布式系统就是将一个完整的系统，按照业务功能，拆分成一个个独立的子系统，对于后端服务器开发人员来说，SOA微服务的架构想必肯定不陌生，它的好处自不必多说。

那分布式系统有什么难题和挑战呢？

让我们设想一个具体的场景，比如三个人讨论中午去哪里吃饭，第一个人说附近刚开了一个火锅店，听说味道非常不错；但第二个人说，不好，吃火锅花的时间太久了，还是随便喝点粥算了；

而第三个人说，那个粥店我昨天刚去过，太难喝了，还不如去吃麦当劳。结果，三个人僵持不下，始终达不成一致。

有人说，这还不好解决，投票呗。于是三个人投了一轮票，结果每个人仍然坚持自己的提议，问题还是没有解决。

有人又想了个主意，干脆我们选出一个leader，这个leader说什么，我们就听他的，这样大家就不用争了。

于是，大家开始投票选leader。结果很悲剧，每个人都觉得自己应该做这个leader。三个人终于发现，「选leader」这件事仍然和原来的「去哪里吃饭」这个问题在本质上是一样的，同样难以解决。

 ACID：

事务四个特性，原子性（Atomicity）、一致性（Consistency）、隔离性（Isolation）和持久性（Durability），

众所周知，同时满足这四个特性才能保证系统的完整性。

那在分布式系统中，还可以同时满足这四个特性吗？

CAP定理：

指的是在一个分布式系统中， Consistency（一致性）、 Availability（可用性）、Partition tolerance（分区容错性），三者不可得兼。

但是分布式系统必然会有多个节点，每个节点都有自己的事务要求，所有分区容错性不能放弃。

因此在C和A之间的抉择就是分布式系统需要解决的根本问题。

BASE理论：

BASE是Basically Available（基本可用）、Soft state（软状态）和Eventually consistent（最终一致性）三个短语的简写，

也是对 CAP定理中的一致性和可用性进行一个权衡的结果。

分布式系统就是为了提高系统的HA，所有解决一致性问题(consensus problem)是分布式系统面临的一个核心问题。

下面我们就来看看常用的一致性协议与算法。

 

二：一致性协议与算法

1：2PC

两阶段提交过程：

阶段一：提交事务请求（投票阶段）

　　1：事务询问：协调者向所有的参与者发送事务内容，询问是否可以执行事务提交，等待参与者相应。

　　2：执行事务：各节点参与者执行本地事务，并记录Undo和Redo日志（未commit）

　　3：参与者反馈事务询问：如果成功执行事务，向协调者反馈Yes，否则反馈No

阶段二：执行事务提交（）

　　如果阶段一反馈都是Yes，则：

　　　　1：协调者发起事务提交请求

　　　　2：参与者提交事务（commit）

　　　　3：反馈事务提交结果

　　　　4：完成事务（根据上一步结果确定）

　　如果阶段一有反馈No，则：

　　　　1：协调者发送回滚请求

　　　　2：参与者事务回滚（rollback）

　　　　3：返回回滚事务结果

　　　　4：中断事务

优点：原理简单，实现方便

缺点：同步阻塞（事务操作全部处于阻塞状态，对于分布式系统来说，限制性能）

　　　单点问题（协调者单点）

　　   数据不一致（阶段二参与者真正执行commit时，不能保证所有节点都成功commit）

 

2：3PC

其实理解了2PC，就很容易理解3PC了

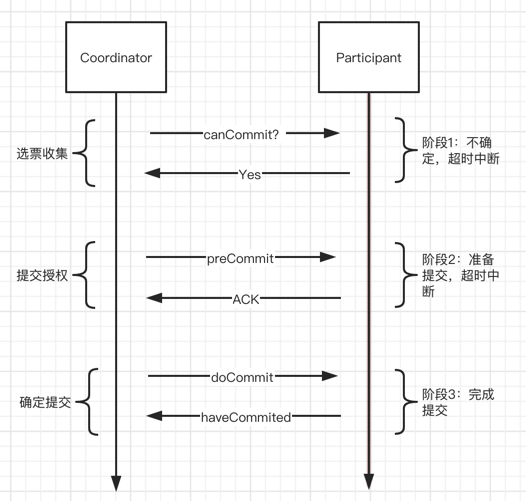
简单的画了三阶段提交的流程图，它其实就是二阶段提交的改进版，将2PC的阶段一（提交事务请求）分成了两步，CanCommit和PreCommit。

相比2PC，3PC最大的优点是降低了参与者事务提交的阻塞范围，但是同2PC一样还是可能出现数据不一致的问题。

 

3：Paxos

说到一致性算法就不得不说大名鼎鼎的Paxos了，（Chubby的作者曾说过：世上只有一种一致性算法，就是Paxos）。

在了解Paxos算法之前，先了解一下拜占庭将军问题(Byzantine Generals Problem)。这个问题也是由Paxos的作者Leslie Lamport提出的。

拜占庭帝国的有许多支军队分开驻扎，每一支军队由一位拜占庭将军(Byzantine general)率领。

为了制定出一个统一的作战计划，每一位将军需要通过信差(messenger)与其它将军互通消息。但是，在拜占庭将军之间可能出现了叛徒(traitor)。

这些叛徒将军的目的是阻挠其他忠诚的将军(loyal generals)达成一致的作战计划。为了这一目的，他们可能做任何事，比如串通起来，故意传出虚假消息，或者不传出任何消息。

这就是著名的 ”拜占庭将军问题“。

我们来看一个简单的例子。假设有5位将军，他们投票来决定是进攻还是撤退。其中两位认为应该进攻，还有两位认为应该撤退，这时候进攻和撤退的票数是2:2打平了。

第五位将军恰好是个叛徒，他告诉前两位应该进攻，但告诉后两位应该撤退，结果前两位将军最终决定进攻，而后两位将军却决定撤退。没有达成一致的作战计划。

要解决这个问题，我们是希望能找到一个算法，保证在存在叛徒阻挠的情况下，我们仍然能够达成如下目标：

• A. 所有忠诚的将军都得到了相同（一致）的作战计划。比如都决定进攻，或都决定撤退，而不是有些将军认为应该进攻，其他将军却决定撤退。
• B. 忠诚的将军不仅得到了相同的作战计划，还应该保证得到的作战计划是合理的(reasonable)。比如，本来进攻是更有利的作战计划，但由于叛徒的阻挠，最终却制定出了一起撤退的计划。这样我们的算法也算失败了。

可以看出，上面的目标A，是比较明确的，至少给定一个算法很容易判定它有没有达到这个目标。但目标B却让人无从下手。一个作战计划是不是「合理」的，本来就不好定义。

即使没有叛徒的存在，忠诚的将军们也未必就一定能制定出合理的计划。这涉及到科学研究中一个非常重要的问题，如果一个事情不能用一种形式化的方式清晰的定义出来，

对于它的研究也就无从谈起，这个事情本身也无法上升到科学的层面。Lamport在对拜占庭将军问题的研究中，一个突出的贡献就是，把这个看似不太好界定的问题，

巧妙地归约到了一个能用数学语言精确描述的问题上去。下面我们就看一下这个过程是怎么做的。

首先我们考虑一下将军们制定作战计划的过程（先假设没有叛徒）。每一位将军根据自己对战局的观察，给出他建议的作战计划——是进攻还是撤退，这称为作战提议。

然后，每位将军把自己的作战提议通过信差传达给其他每一位将军。现在每一位将军都知道了其他将军的作战提议，再加上他自己的作战提议，他需要根据所有这些信息得到最终的一个作战计划。

为了表达上更清晰，我们给每位将军进行编号，分别是1, 2, …, n，每位将军提出的作战提议记为v(1), v(2), …, v(n)，一共是n个值，这其中有些代表「进攻」，有些代表「撤退」。

经过信差传递消息之后，每位将军都看到了相同的作战提议序列v(1), v(2), …, v(n)，当然这其中的一个是当前这位将军自己提出来的。

然后只要每位将军采用同样的方法，对所有的v(1), v(2), …, v(n)这些信息进行汇总，就能得到同样的最终作战计划。

比如，容易想到的一个方法是投票法，即对v(1), v(2), …, v(n)中不同的作战提议进行投票，最后选择得票最多的作为最终作战计划。

当然，这样得到的最终作战计划也不能保证就是最好的，但这应该是我们能做到的最好的了。我们现在仍然假设将军里没有叛徒。

我们发现，前面提到的目标A和目标B的要求可以适当「降低」一些：我们不再关注将军们是否能达成最终一致的作战计划，并且这个计划是不是「合理」；

我们只关注每个将军是否收到了完全相同的作战提议v(1), v(2), …, v(n)。只要每位将军收到的这些作战提议是完全相同的，他们再用同样的方法进行汇总，就很容易得到最终一致的作战计划。

至于这个最终的作战计划是不是最好的，那就跟很多「人为」的因素有关了，我们不去管它。

现在我们考虑将军中出现了叛徒。遵循前面的思路，我们仍然希望每位将军能够收到完全相同的作战提议v(1), v(2), …, v(n)。

现在我们仔细审视一下其中的一个值，v(i)，在前面的描述中，它表示来自第i个将军的作战提议。如果第i个将军是忠诚的，那么这个定义没有什么问题。

但是，如果第i个将军是叛徒，那么就有问题了。为什么呢？因为叛徒可以为所欲为，他为了扰乱整个作战计划的制定，完全可能向不同的将军给出不同的作战提议。

这样的话，不同的忠诚将军收到的来自第i个将军的v(i)可能是不同的值。这样v(i)这个定义就不对了，它需要改一改。

不管怎么样，即使存在叛徒，我们还是希望每位将军最终是基于完全相同的作战提议来做汇总，这些作战提议仍然记为v(1), v(2), …, v(n)。

不过，这里的v(i)不再表示来自第i个将军的作战提议，而是表示经过我们设计的某个一致性算法处理之后，每位将军最终看到的第i个提议。

这里需要分两种情况讨论。首先第一种情况，如果第i个将军是忠诚的，那么我们自然希望这个v(i)就是第i个将军发送出来的作战提议。

换句话说，我们希望经过一致性算法处理之后，第i个将军如果是忠诚的，那么它的提议能够被如实地传达给其他将军，而不会被叛徒的行为所干扰。

这是可能制定出「合理」作战计划的前提。第二种情况，如果第i个将军是叛徒，那么他有可能向不同的将军发送不同的提议。

这时候我们不能够只听他的一面之词，而是希望经过一致性算法处理之后，各个将军之间充分交换意见，然后根据其他各个将军转述的信息，综合判断得到一个v(i)。

这个v(i)是进攻还是撤退，并不太重要，关键是要保证每位将军得到的v(i)是相同的。只有这样，各位将军经过汇总所有的v(1), v(2), …, v(n)之后才能得到最终的完全一致的作战计划。

根据上面的分析，我们发现，在这两种情况中，我们都只需要关注单个将军（也就是第i个将军）所发出的提议如何传达给其他将军。重点终于来了！

至此，我们就能够把原来的问题归约到一个子问题上。这个子问题，才是Leslie Lamport在他的论文中被真正命名为「拜占庭将军问题(Byzantine Generals Problem)」的那个问题。

在这个问题中，我们只关注发送命令的单个将军，称他为主将(commanding general)，而其他接受命令的将军称为副官(lieutenant)。下面是「拜占庭将军问题」的精确描述。

一个主将发送命令给n-1个副官，如何才能确保下面两个条件：

• (IC1) 所有忠诚的副官最终都接受相同的命令。
• (IC2) 如果主将是忠诚的，那么所有忠诚的副官都接受主将发出的命令。

这其实正好对应了我们前面已经讨论过的两种情况。如果主将是忠诚的，那么条件IC2保证了命令如实地传递，这时候条件IC1自然也满足了；

如果主将是叛徒，那么条件IC2没有意义了，而条件IC1保证了，即使叛徒主将对每个副官发出不同的命令，每个副官仍然能最终获得一致的命令。

这里有两个地方可能让人产生疑惑。

第一，有些人会问了，难道主将还能是叛徒？主将都是叛徒了，还有啥搞头啊？其实是这样的，这个「拜占庭将军问题」只是原问题的一个子问题。

当n个将军通过传递消息来决策作战计划的时候，可以分解成n个「拜占庭将军问题」，即分别以每位将军作为主将，以其余n-1位将军作为副官。

如果有一个算法能够解决「拜占庭将军问题」，那么同时运行n个算法实例，就能使得每位将军都获得完全相同的作战提议序列，即前面我们提到的v(1), v(2), …, v(n)。

最后，每位将军将v(1), v(2), …, v(n)使用相同的方法进行汇总（比如按多数投票），就能得到最终的作战计划。

第二，当主将是叛徒的时候，他可以向不同的副官发送不同的命令，怎么可能每个副官仍然能最终获得一致的命令呢？这正是算法需要解决的。

其实这也容易解释（我们前面也提到过这个思路），由于主将可能向不同的副官发送不同的命令，所以副官不能直接采用主将发来的命令，而是也要看看其他副官转述来的主将的命令是什么。

然后，一个副官综合了由所有副官转述的命令（再加上主将直接发来的命令）之后，就可能得到比较全面的信息，从而做出一致的判断（在实际中是个不断迭代的过程）。

好了，我们用了这么多篇幅，终于把「拜占庭将军问题」本身描述清楚了。这实际上也是最难的部分。

只要问题本身分析清楚了，如何设计一个能解决它的算法就只是细节问题了。我们这里不深入算法的细节了，感兴趣的读者可以去查阅下列论文：

• 《The Byzantine Generals Problem》，下载地址：http://lamport.azurewebsites.net/pubs/byz.pdf
• 《Reaching Agreement in the Presence of Faults》，下载地址：http://lamport.azurewebsites.net/pubs/reaching.pdf

我们这里只提一下论文给出的算法的结论。

使用不同的消息模型，「拜占庭将军问题」有不同的解法。

• 如果将军之间使用口头消息(oral messages)，也就是说，消息被转述的时候是可能被篡改的，那么要对付m个叛徒，需要至少有3m+1个将军（其中至少2m+1个将军是忠诚的）。
• 如果将军之间使用签名消息(signed messages)，也就是说，消息被发出来之后是无法伪造的，只要被篡改就会被发现，那么对付m个叛徒，只需要至少m+2个将军，也就是说至少2个忠诚的将军（如果只有1个忠诚的将军，显然这个问题没有意义）。这种情况实际相当于对忠诚将军的数目没有限制。

 

事实上，大多数分布式系统都是在一个局域网中，所以消息被篡改或者消息不完整都是可以排除或者避免的。

而Paxos算法（Paxos Made Simple）就解决了在消息没有损坏（corrupted）的可信任环境的前提下，保证系统一致性。

根据Paxos的论文所说，Paxos的设计是基于异步(asynchronous)、非拜占庭(non-Byzantine)的系统模型，即：

• 节点可以以任意速度运行，可能宕机、重启。但是，算法执行过程中需要记录的一些变量，在重启后应该能够恢复。
• 消息可以延迟任意长时间，可以重复(duplicated)，可以丢失(lost)，但不能损坏(corrupted)。

通常把能够处理拜占庭错误的这种容错性称为「Byzantine fault tolerance」，简称为BFT。

BFT的算法应该可以解决任何错误下的分布式一致性问题，也包括Paxos所解决的问题，而Paxos只能容忍非拜占庭错误。

但是，在只有非拜占庭错误出现的前提下，Paxos基于异步模型，是比同步模型更弱的系统假设，因此算法更鲁棒(Robust)。当然，Paxos也更高效。

Google Chubby 是基于Paxos算法的一个工程实践。

 

4：Raft

Raft is a consensus algorithm for managing a replicated log.

继续阅读之前，先看一下Raft动画原理（http://thesecretlivesofdata.com/raft/）

在Raft中，节点有三种角色：

• Leader：负责接收客户端的请求，将日志复制到其他节点并告知其他节点何时应用这些日志是安全的

• Candidate：用于选举Leader的一种角色

• Follower：负责响应来自Leader或者Candidate的请求

　　　　　　　　　　　　　　不同角色之间的转换

 

 Raft实现一致性的最重要两个功能就是：

1. 选主 Leader Election
2. 复制日志 Log Replication

Redis中哨兵集群中的哨兵领导者选举和Redis-Cluster中的主节点选举都是基于Raft算法实现的。

 

5：ZAB

作为一个高效且可靠分布式协调服务，Zookeeper可谓是大名鼎鼎，提供了诸如统一命名服务，配置管理，分布式锁等基础服务。

Zookeeper集群没有采用典型的Master\Slave模式，而是引入了Leader、Follower、Observer三种角色，

其中Leader为客户端提供读和写服务，而Follower和Observer只提供读服务，两者区别是，Observer不参与Leader选举。

ZAB(ZooKeeper Atomic Broadcast)是为ZooKeeper专门设计的一种支持崩溃恢复的原子广播协议。

ZAB协议对数据事务的处理请求方式为：

所有事务请求必须由一个全局唯一的服务器来协调处理，这个服务器被称为Leader（只有一个），而余下的服务器被称为Follower。

Leader负责将一个客户端的事务请求转换为一个事务提议（Proposal），并将该Propsal分发给集群中的所有Follower。

之后等待所有Follower的反馈，一旦超过单数的Follower进行了正确的反馈，那么Leader会再次向所有Follower发起Commit消息，

要求将上一次Proposal进行提交。

消息广播：

类似于2PC的原子广播协议，由Leader将事务Proposal分发给集群中的所有Follower，Leader收集Follower的ACK，最后进行事务提交（commit）。

其中Leader会保证每个事务Proposal都有一个全局递增的唯一ID（ZXID），而且Leader分发给Follower的消息会放入一个单独的队列里，保证消息FIFO。

但与2PC不同的是，Follower对Leader发起的Proposal的反馈，要么是正常反馈，要么就抛弃Leader。

这意味着Leader在收到超过一半的Follower的正常反馈后，就可以继续提交事务的commit了。

好处是可用性更高，但是如果Leader崩溃了，那么很多Follwer出现数据不一致，整个集群数据也就不一致了。

崩溃恢复

为了解决Leader崩溃，出现的数据不一致情况，因此需要一个可靠高效的Leader选举算法。

初始阶段Leader选举

　　此时节点状态为election，投票（myid,ZXID），ZXID大的优先作为Leader，如果ZXID相同myid大的优先作为Leader，

　　此时服务器状态分别为leading、following。

运行期间Leader选举

　　当Leader崩溃后，开始Leader选举，首先服务器状态改变，所有非Observer服务器状态变为looking，

　　同样节点发起投票（myid,ZXID），统计投票，最后选出Leader。　

从3.4.0版本开始，ZooKeeper的选举算法只保留了TCP版本的FastLeaderElection算法。

（算法实现细节，可以参考：ZooKeeper’s atomic broadcast protocol：http://www.tcs.hut.fi/Studies/T-79.5001/reports/2012-deSouzaMedeiros.pdf）

 

三：参考文献

1：《从 Paxos 到 Zookeeper——分布式一致性原理和实践》

2：漫谈分布式系统、拜占庭将军问题与区块链

3：共识算法：Raft