CVPR 2020 三篇有趣的论文解读
ManWingloeng 人气:1
**作者 | 文永亮**
**学校 | 哈尔滨工业大学(深圳)**
**研究方向 | 视频预测、时空序列预测**
## 目录
- **AdderNet** — 其实不需要这么多乘法
- **Deep Snake for Real-Time Instance Segmentation** — 用轮廓做实例分割
- **Blurry Video Frame Interpolation** — 完美的金字塔
## AdderNet (在深度学习中我们真的需要乘法?)

这篇论文是北大、诺亚、鹏城、悉大的论文,观点比较有趣,在喜提**CVPR2020**之前也比较火了,下面我可以介绍一下。
论文指出我们可以定义如下公式,首先我们定义核大小为d,输入通道为$c_{in}$,输出通道为$c_{out}$的滤波器$F \in \mathbb{R}^{d \times d \times c_{i n} \times c_{o u t}}$,长宽为H, W 的输入特征为$X \in \mathbb{R}^{H \times W \times c_{i n}}$,
$$
Y(m, n, t)=\sum_{i=0}^{d} \sum_{j=0}^{d} \sum_{k=0}^{c_{i n}} S(X(m+i, n+j, k), F(i, j, k, t))
$$
其中 $S(\cdot, \cdot)$ 为相似度计算方法,如果设 $S(x, y)=x×y$ ,这就是卷积的一种定义方法了。 那么论文就引出加法网络的基本算子如何定义的:
$$
Y(m, n, t)=-\sum_{i=0}^{d} \sum_{j=0}^{d} \sum_{k=0}^{c_{i n}}|X(m+i, n+j, k)-F(i, j, k, t)|
$$
如上定义只用了加法的$\ell{1}$距离,可以有效地计算滤波器和特征之间的相似度。
在CIFAR-10和CIFAR-100以及ImageNet的实验结果:
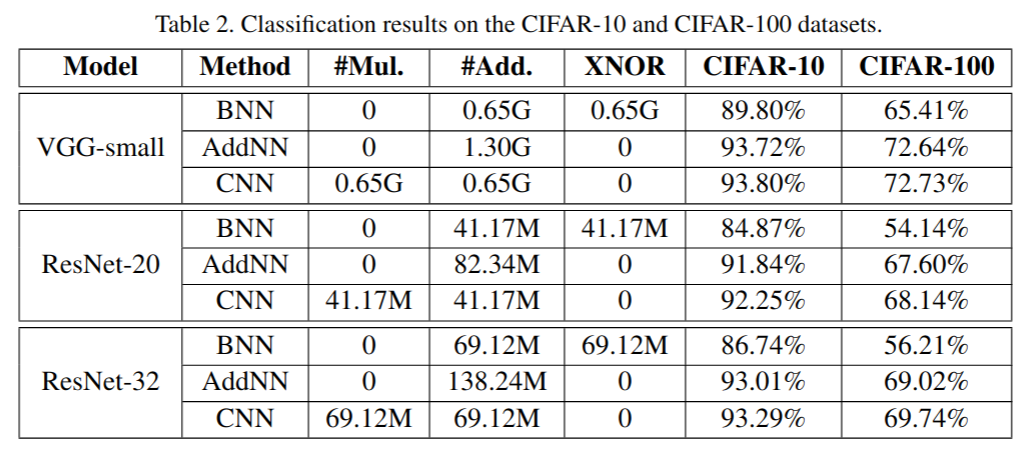
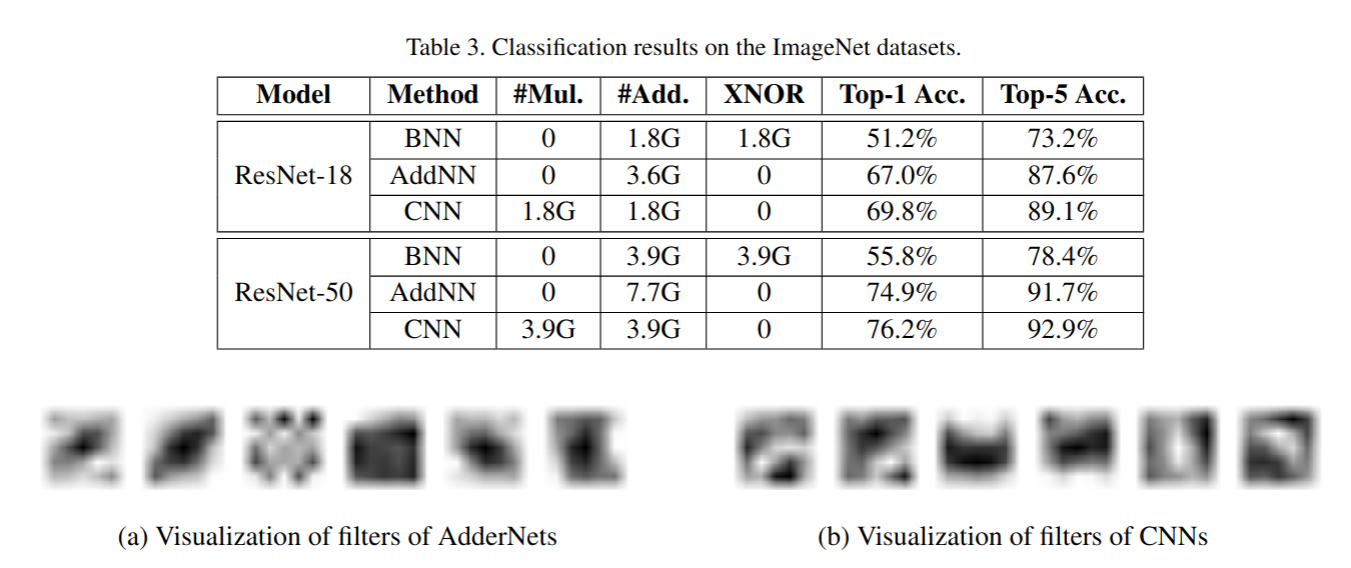
可以看到在把卷积替换成加法之后好像也没有太多精度的丢失,正如标题说的,我们真的需要这么多乘法吗?
## Deep Snake用于实例分割

这篇工作是来自浙江大学Deepwise AI Lab的,我起初看到感觉十分有趣,这篇论文的实例分割并不是每个像素的去分,而是用轮廓围住了实例。代码已经开源,有兴趣的同学可以去看看。
repo url:https://github.com/zju3dv/snake
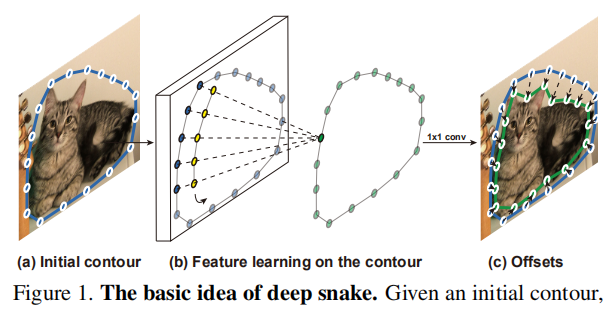 基本思想是给实例一个初始轮廓,用循环卷积**(Circular Convolution)**方法学习更新轮廓,最后得到offsets。
我在下面介绍一下**Circular Convolution**:
基本思想是给实例一个初始轮廓,用循环卷积**(Circular Convolution)**方法学习更新轮廓,最后得到offsets。
我在下面介绍一下**Circular Convolution**:
 $$
\left(f_{N}\right)_{i} \triangleq \sum_{j=-\infty}^{\infty} f_{i-j N}=f_{i(\bmod N)}\\
\left(f_{N} * k\right)_{i}=\sum_{j=-r}^{r}\left(f_{N}\right)_{i+j} k_{j}
$$
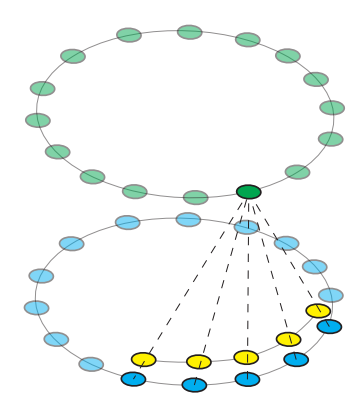
我们定义特征为蓝色部分的圆圈,那么它可以表达为$f_{i(\bmod N)}$ ,*是标准的卷积操作,整个循环卷积就是每一个蓝色的特征与黄色的kernel相乘得到对应高亮的绿色输出,一圈下来就得到完整的输出,kernel也是共享的。

我们可以通过图(b)看到整个算法的pipeline,首先输入图片,实验中使用了CenterNet作为目标检测器, Center Net将检测任务重新定义为关键点检测问题,这样得到一个初始的box,然后取每边的中点连接作为初始的**Diamond contour**(实际实验中作者说他upsample成了40个点),然后通过变形操作使点回归到实例的边界点,然后通过边界点一半向外拓展1/4的边长得到一个**Octagon contour(八边形轮廓)**,再做变形操作最终回归到目标的形状边界。
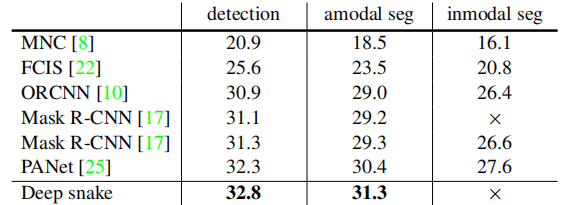
作者在三个数据集上做了实验,分别是**Cityscapes, Kins, Sbd**。可以看到在Kins上的数据集的AP值比Mask RCNN好一些。
$$
\left(f_{N}\right)_{i} \triangleq \sum_{j=-\infty}^{\infty} f_{i-j N}=f_{i(\bmod N)}\\
\left(f_{N} * k\right)_{i}=\sum_{j=-r}^{r}\left(f_{N}\right)_{i+j} k_{j}
$$
我们定义特征为蓝色部分的圆圈,那么它可以表达为$f_{i(\bmod N)}$ ,*是标准的卷积操作,整个循环卷积就是每一个蓝色的特征与黄色的kernel相乘得到对应高亮的绿色输出,一圈下来就得到完整的输出,kernel也是共享的。

我们可以通过图(b)看到整个算法的pipeline,首先输入图片,实验中使用了CenterNet作为目标检测器, Center Net将检测任务重新定义为关键点检测问题,这样得到一个初始的box,然后取每边的中点连接作为初始的**Diamond contour**(实际实验中作者说他upsample成了40个点),然后通过变形操作使点回归到实例的边界点,然后通过边界点一半向外拓展1/4的边长得到一个**Octagon contour(八边形轮廓)**,再做变形操作最终回归到目标的形状边界。
作者在三个数据集上做了实验,分别是**Cityscapes, Kins, Sbd**。可以看到在Kins上的数据集的AP值比Mask RCNN好一些。
 其分割的效果也不错且有点有趣:
其分割的效果也不错且有点有趣:
 可以看到确实挺快的, Sbd数据集的512 *×* 512 的图片,在Intel i7 3.7GHz,GTX 1080 Ti GPU达到32.3 fps。
可以看到确实挺快的, Sbd数据集的512 *×* 512 的图片,在Intel i7 3.7GHz,GTX 1080 Ti GPU达到32.3 fps。
 ## BIN 模糊视频插帧

这篇paper是上海交通大学的翟广涛教授组的模糊视频插帧技术,主要是为了提高视频质量并且达到插帧的效果,我觉得这篇论文十分优秀,只可惜代码还在重构中,repo说6.14公布,这也有点久啊。
repo url : *https://github.com/laomao0/BIN*
这篇论文设计的很精巧,模型构建中分为两块:
- **1.金字塔模块**
- **2.金字塔间的递归模块**
如下图所示:
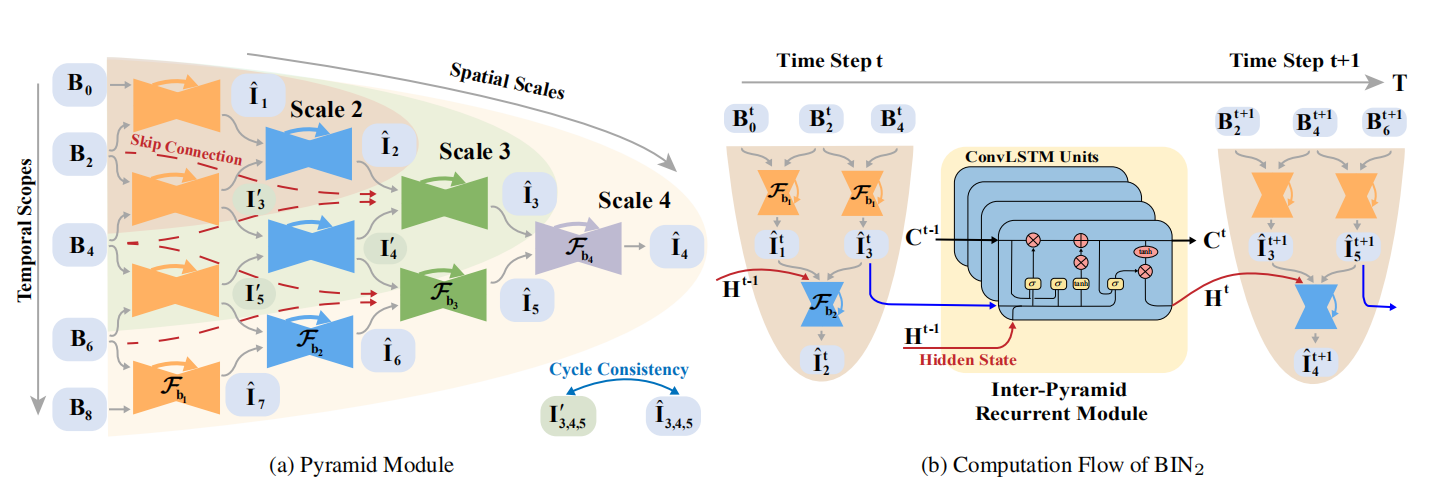
其实这网络结构很容易理解,$B_0,B_2,B_4,B_6,B_8$都是输入,当我们取Scale 2的时候,输入取$B_0,B_2,B_4$, 我们可通过$B_0,B_2$得到中间插帧$\hat{{I}}_1$,同理可得$\hat{I}_3$,最后通过$\hat{{I}}_1$和$\hat{I}_3$插帧得到$\hat{{I}}_2$。
数学表达如下:
$$
\hat{\mathbf{I}}_{1: 1: 2 N-1}=\mathcal{F}\left(\mathbf{B}_{0: 2: 2 N}\right)
$$
$$
\hat{\mathbf{I}}_{1}=\mathcal{F}_{\mathrm{b}}\left(\mathbf{B}_{0}, \mathbf{B}_{2}\right)
$$
但是Scale 3和4的时候就不一样了,我举例Scale 3的时候,Scale 4同理
$$
\hat{\mathbf{I}}_{1}=\mathcal{F}_{\mathrm{b_1}}\left(\mathbf{B}_{0}, \mathbf{B}_{2}\right)\\
{\mathbf{I'}}_{3}=\mathcal{F}_{\mathrm{b_1}}\left(\mathbf{B}_{2}, \mathbf{B}_{4}\right)\\
\hat{\mathbf{I}}_{2}=\mathcal{F}_{\mathrm{b_2}}\left(\mathbf{\hat{I}}_{1}, \mathbf{I'}_{3}\right)\\
\hat{\mathbf{I}}_{3}=\mathcal{F}_{\mathrm{b_2}}\left(\mathbf{\hat{I}}_{2}, \mathbf{\hat{I}}_{4},\mathbf{B}_{3},\mathbf{B}_{4}\right)\\
{\mathbf{I'}}_{5}=\mathcal{F}_{\mathrm{b_1}}\left(\mathbf{B}_{4}, \mathbf{B}_{6}\right)
$$
这样通过$B_0,B_2,B_4,B_6$就会得到中间1,3,5的插帧,或许有人疑惑为什么会有$\mathbf{I'}_{3}$ 和$\hat{\mathbf{I}}_{3}$ ,这两个有什么区别,这里主要就是因为作者做了一个Cycle Consistency的loss,主要是保证中间产生的帧与金字塔最后产生的帧保持空间上的一致性。
## BIN 模糊视频插帧

这篇paper是上海交通大学的翟广涛教授组的模糊视频插帧技术,主要是为了提高视频质量并且达到插帧的效果,我觉得这篇论文十分优秀,只可惜代码还在重构中,repo说6.14公布,这也有点久啊。
repo url : *https://github.com/laomao0/BIN*
这篇论文设计的很精巧,模型构建中分为两块:
- **1.金字塔模块**
- **2.金字塔间的递归模块**
如下图所示:

其实这网络结构很容易理解,$B_0,B_2,B_4,B_6,B_8$都是输入,当我们取Scale 2的时候,输入取$B_0,B_2,B_4$, 我们可通过$B_0,B_2$得到中间插帧$\hat{{I}}_1$,同理可得$\hat{I}_3$,最后通过$\hat{{I}}_1$和$\hat{I}_3$插帧得到$\hat{{I}}_2$。
数学表达如下:
$$
\hat{\mathbf{I}}_{1: 1: 2 N-1}=\mathcal{F}\left(\mathbf{B}_{0: 2: 2 N}\right)
$$
$$
\hat{\mathbf{I}}_{1}=\mathcal{F}_{\mathrm{b}}\left(\mathbf{B}_{0}, \mathbf{B}_{2}\right)
$$
但是Scale 3和4的时候就不一样了,我举例Scale 3的时候,Scale 4同理
$$
\hat{\mathbf{I}}_{1}=\mathcal{F}_{\mathrm{b_1}}\left(\mathbf{B}_{0}, \mathbf{B}_{2}\right)\\
{\mathbf{I'}}_{3}=\mathcal{F}_{\mathrm{b_1}}\left(\mathbf{B}_{2}, \mathbf{B}_{4}\right)\\
\hat{\mathbf{I}}_{2}=\mathcal{F}_{\mathrm{b_2}}\left(\mathbf{\hat{I}}_{1}, \mathbf{I'}_{3}\right)\\
\hat{\mathbf{I}}_{3}=\mathcal{F}_{\mathrm{b_2}}\left(\mathbf{\hat{I}}_{2}, \mathbf{\hat{I}}_{4},\mathbf{B}_{3},\mathbf{B}_{4}\right)\\
{\mathbf{I'}}_{5}=\mathcal{F}_{\mathrm{b_1}}\left(\mathbf{B}_{4}, \mathbf{B}_{6}\right)
$$
这样通过$B_0,B_2,B_4,B_6$就会得到中间1,3,5的插帧,或许有人疑惑为什么会有$\mathbf{I'}_{3}$ 和$\hat{\mathbf{I}}_{3}$ ,这两个有什么区别,这里主要就是因为作者做了一个Cycle Consistency的loss,主要是保证中间产生的帧与金字塔最后产生的帧保持空间上的一致性。
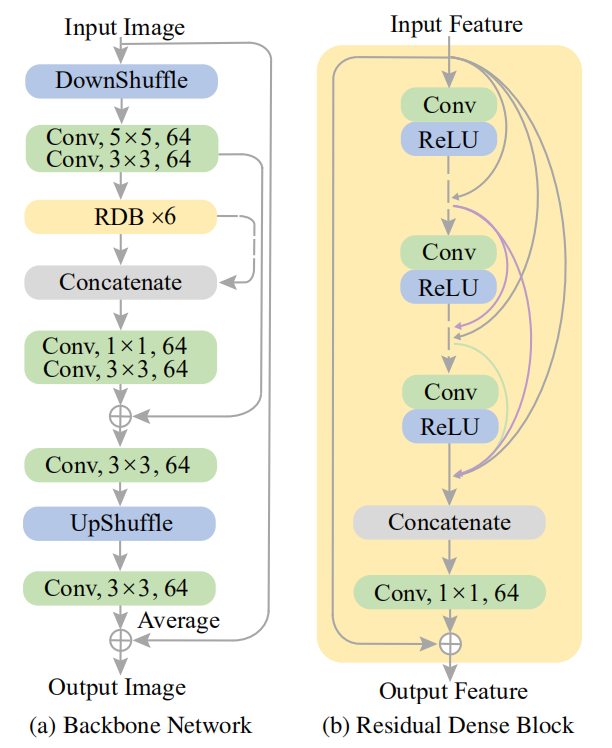
金字塔模块的构建有(a)Backbone (b)Residual Dense Block 两种
其中**金字塔模块**具有可调节的空间感受域和时间范围,可以从图中看到,作者采用了三种scale,随着scale的增加,网络将会拓展的更深,因此具有更大的空间感受域,同时在时间范围内输入的数量会需要更多,所以说时间范围也正是如此,从而控制计算复杂度和复原能力。金字塔模块使用普通的卷积神经网络搭建而成,其中同一级的共享权重,这其实节省了很多参数空间,但是这样是否就缺乏了时间上的信息呢?
如果采用Scale 2的时候,我们可以分析金字塔之间如何传递信息的,如图中(b)部分:
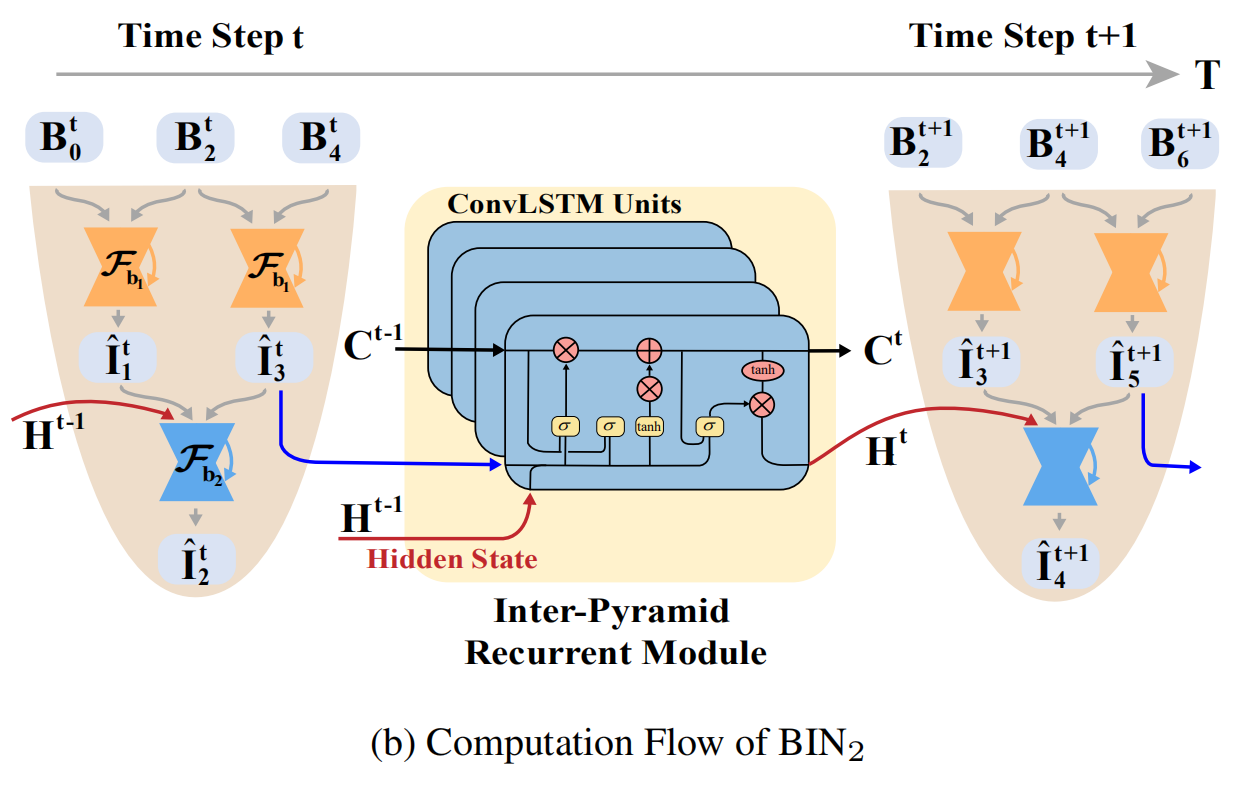 **ConvLSTM**构成的**Inter-Pyramid Recurrent Module**实际上就是为了传递时空上的信息,这里Time Step为2,$B_2^{t}$ 与$B_2^{t+1}$ 实际上是同一张输入,但是进入了两个不同的模块,整体step前进了一步,其中的ConvLSTM就是为了传递C和H的,其公式如下:
$$
\mathbf{H}^{t}, \mathbf{C}^{t}=\mathcal{F}_{\mathrm{c}}\left(\hat{\mathbf{I}}_{3}^{t}, \mathbf{H}^{t-1}, \mathbf{C}^{t-1}\right)
$$
**损失函数非常的简单**,这里不做过多的说明,分为了重构误差$L_p$ **(Pixel Reconstruction)** 和 一致性误差$L_c$ **(Cycle Consistency)** :
$$
\rho(x)=\sqrt{x^{2}+\epsilon^{2}}\\
\mathcal{L}_{p}=\frac{1}{T} \sum_{t=1}^{T} \sum_{n=1}^{2 M-1} \rho\left(\hat{\mathbf{I}}_{n}^{t}-\mathbf{G}_{n}^{t}\right)\\
\mathcal{L}_{c}=\frac{1}{T} \sum_{t=1}^{T} \sum_{n \in \Omega} \rho\left(\mathbf{I}_{n}^{t}-\hat{\mathbf{I}}_{n}^{t}\right)\\
\mathcal{L}=\mathcal{L}_{p}+\mathcal{L}_{c}\\
$$
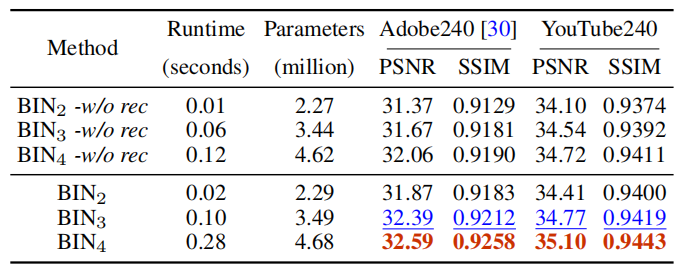
**数据集**用的是:**Adobe240**和**YouTube240**,可以看到论文的效果取了Scale=4的时候跟GT已经看不出太大的区别了。
**ConvLSTM**构成的**Inter-Pyramid Recurrent Module**实际上就是为了传递时空上的信息,这里Time Step为2,$B_2^{t}$ 与$B_2^{t+1}$ 实际上是同一张输入,但是进入了两个不同的模块,整体step前进了一步,其中的ConvLSTM就是为了传递C和H的,其公式如下:
$$
\mathbf{H}^{t}, \mathbf{C}^{t}=\mathcal{F}_{\mathrm{c}}\left(\hat{\mathbf{I}}_{3}^{t}, \mathbf{H}^{t-1}, \mathbf{C}^{t-1}\right)
$$
**损失函数非常的简单**,这里不做过多的说明,分为了重构误差$L_p$ **(Pixel Reconstruction)** 和 一致性误差$L_c$ **(Cycle Consistency)** :
$$
\rho(x)=\sqrt{x^{2}+\epsilon^{2}}\\
\mathcal{L}_{p}=\frac{1}{T} \sum_{t=1}^{T} \sum_{n=1}^{2 M-1} \rho\left(\hat{\mathbf{I}}_{n}^{t}-\mathbf{G}_{n}^{t}\right)\\
\mathcal{L}_{c}=\frac{1}{T} \sum_{t=1}^{T} \sum_{n \in \Omega} \rho\left(\mathbf{I}_{n}^{t}-\hat{\mathbf{I}}_{n}^{t}\right)\\
\mathcal{L}=\mathcal{L}_{p}+\mathcal{L}_{c}\\
$$
**数据集**用的是:**Adobe240**和**YouTube240**,可以看到论文的效果取了Scale=4的时候跟GT已经看不出太大的区别了。
 而且**Scale越大图片质量就越好**:
而且**Scale越大图片质量就越好**:
 基本思想是给实例一个初始轮廓,用循环卷积**(Circular Convolution)**方法学习更新轮廓,最后得到offsets。
我在下面介绍一下**Circular Convolution**:
基本思想是给实例一个初始轮廓,用循环卷积**(Circular Convolution)**方法学习更新轮廓,最后得到offsets。
我在下面介绍一下**Circular Convolution**:
 $$
\left(f_{N}\right)_{i} \triangleq \sum_{j=-\infty}^{\infty} f_{i-j N}=f_{i(\bmod N)}\\
\left(f_{N} * k\right)_{i}=\sum_{j=-r}^{r}\left(f_{N}\right)_{i+j} k_{j}
$$
我们定义特征为蓝色部分的圆圈,那么它可以表达为$f_{i(\bmod N)}$ ,*是标准的卷积操作,整个循环卷积就是每一个蓝色的特征与黄色的kernel相乘得到对应高亮的绿色输出,一圈下来就得到完整的输出,kernel也是共享的。

我们可以通过图(b)看到整个算法的pipeline,首先输入图片,实验中使用了CenterNet作为目标检测器, Center Net将检测任务重新定义为关键点检测问题,这样得到一个初始的box,然后取每边的中点连接作为初始的**Diamond contour**(实际实验中作者说他upsample成了40个点),然后通过变形操作使点回归到实例的边界点,然后通过边界点一半向外拓展1/4的边长得到一个**Octagon contour(八边形轮廓)**,再做变形操作最终回归到目标的形状边界。
作者在三个数据集上做了实验,分别是**Cityscapes, Kins, Sbd**。可以看到在Kins上的数据集的AP值比Mask RCNN好一些。
$$
\left(f_{N}\right)_{i} \triangleq \sum_{j=-\infty}^{\infty} f_{i-j N}=f_{i(\bmod N)}\\
\left(f_{N} * k\right)_{i}=\sum_{j=-r}^{r}\left(f_{N}\right)_{i+j} k_{j}
$$
我们定义特征为蓝色部分的圆圈,那么它可以表达为$f_{i(\bmod N)}$ ,*是标准的卷积操作,整个循环卷积就是每一个蓝色的特征与黄色的kernel相乘得到对应高亮的绿色输出,一圈下来就得到完整的输出,kernel也是共享的。

我们可以通过图(b)看到整个算法的pipeline,首先输入图片,实验中使用了CenterNet作为目标检测器, Center Net将检测任务重新定义为关键点检测问题,这样得到一个初始的box,然后取每边的中点连接作为初始的**Diamond contour**(实际实验中作者说他upsample成了40个点),然后通过变形操作使点回归到实例的边界点,然后通过边界点一半向外拓展1/4的边长得到一个**Octagon contour(八边形轮廓)**,再做变形操作最终回归到目标的形状边界。
作者在三个数据集上做了实验,分别是**Cityscapes, Kins, Sbd**。可以看到在Kins上的数据集的AP值比Mask RCNN好一些。
 其分割的效果也不错且有点有趣:
其分割的效果也不错且有点有趣:
 可以看到确实挺快的, Sbd数据集的512 *×* 512 的图片,在Intel i7 3.7GHz,GTX 1080 Ti GPU达到32.3 fps。
可以看到确实挺快的, Sbd数据集的512 *×* 512 的图片,在Intel i7 3.7GHz,GTX 1080 Ti GPU达到32.3 fps。
 ## BIN 模糊视频插帧

这篇paper是上海交通大学的翟广涛教授组的模糊视频插帧技术,主要是为了提高视频质量并且达到插帧的效果,我觉得这篇论文十分优秀,只可惜代码还在重构中,repo说6.14公布,这也有点久啊。
repo url : *https://github.com/laomao0/BIN*
这篇论文设计的很精巧,模型构建中分为两块:
- **1.金字塔模块**
- **2.金字塔间的递归模块**
如下图所示:

其实这网络结构很容易理解,$B_0,B_2,B_4,B_6,B_8$都是输入,当我们取Scale 2的时候,输入取$B_0,B_2,B_4$, 我们可通过$B_0,B_2$得到中间插帧$\hat{{I}}_1$,同理可得$\hat{I}_3$,最后通过$\hat{{I}}_1$和$\hat{I}_3$插帧得到$\hat{{I}}_2$。
数学表达如下:
$$
\hat{\mathbf{I}}_{1: 1: 2 N-1}=\mathcal{F}\left(\mathbf{B}_{0: 2: 2 N}\right)
$$
$$
\hat{\mathbf{I}}_{1}=\mathcal{F}_{\mathrm{b}}\left(\mathbf{B}_{0}, \mathbf{B}_{2}\right)
$$
但是Scale 3和4的时候就不一样了,我举例Scale 3的时候,Scale 4同理
$$
\hat{\mathbf{I}}_{1}=\mathcal{F}_{\mathrm{b_1}}\left(\mathbf{B}_{0}, \mathbf{B}_{2}\right)\\
{\mathbf{I'}}_{3}=\mathcal{F}_{\mathrm{b_1}}\left(\mathbf{B}_{2}, \mathbf{B}_{4}\right)\\
\hat{\mathbf{I}}_{2}=\mathcal{F}_{\mathrm{b_2}}\left(\mathbf{\hat{I}}_{1}, \mathbf{I'}_{3}\right)\\
\hat{\mathbf{I}}_{3}=\mathcal{F}_{\mathrm{b_2}}\left(\mathbf{\hat{I}}_{2}, \mathbf{\hat{I}}_{4},\mathbf{B}_{3},\mathbf{B}_{4}\right)\\
{\mathbf{I'}}_{5}=\mathcal{F}_{\mathrm{b_1}}\left(\mathbf{B}_{4}, \mathbf{B}_{6}\right)
$$
这样通过$B_0,B_2,B_4,B_6$就会得到中间1,3,5的插帧,或许有人疑惑为什么会有$\mathbf{I'}_{3}$ 和$\hat{\mathbf{I}}_{3}$ ,这两个有什么区别,这里主要就是因为作者做了一个Cycle Consistency的loss,主要是保证中间产生的帧与金字塔最后产生的帧保持空间上的一致性。
## BIN 模糊视频插帧

这篇paper是上海交通大学的翟广涛教授组的模糊视频插帧技术,主要是为了提高视频质量并且达到插帧的效果,我觉得这篇论文十分优秀,只可惜代码还在重构中,repo说6.14公布,这也有点久啊。
repo url : *https://github.com/laomao0/BIN*
这篇论文设计的很精巧,模型构建中分为两块:
- **1.金字塔模块**
- **2.金字塔间的递归模块**
如下图所示:

其实这网络结构很容易理解,$B_0,B_2,B_4,B_6,B_8$都是输入,当我们取Scale 2的时候,输入取$B_0,B_2,B_4$, 我们可通过$B_0,B_2$得到中间插帧$\hat{{I}}_1$,同理可得$\hat{I}_3$,最后通过$\hat{{I}}_1$和$\hat{I}_3$插帧得到$\hat{{I}}_2$。
数学表达如下:
$$
\hat{\mathbf{I}}_{1: 1: 2 N-1}=\mathcal{F}\left(\mathbf{B}_{0: 2: 2 N}\right)
$$
$$
\hat{\mathbf{I}}_{1}=\mathcal{F}_{\mathrm{b}}\left(\mathbf{B}_{0}, \mathbf{B}_{2}\right)
$$
但是Scale 3和4的时候就不一样了,我举例Scale 3的时候,Scale 4同理
$$
\hat{\mathbf{I}}_{1}=\mathcal{F}_{\mathrm{b_1}}\left(\mathbf{B}_{0}, \mathbf{B}_{2}\right)\\
{\mathbf{I'}}_{3}=\mathcal{F}_{\mathrm{b_1}}\left(\mathbf{B}_{2}, \mathbf{B}_{4}\right)\\
\hat{\mathbf{I}}_{2}=\mathcal{F}_{\mathrm{b_2}}\left(\mathbf{\hat{I}}_{1}, \mathbf{I'}_{3}\right)\\
\hat{\mathbf{I}}_{3}=\mathcal{F}_{\mathrm{b_2}}\left(\mathbf{\hat{I}}_{2}, \mathbf{\hat{I}}_{4},\mathbf{B}_{3},\mathbf{B}_{4}\right)\\
{\mathbf{I'}}_{5}=\mathcal{F}_{\mathrm{b_1}}\left(\mathbf{B}_{4}, \mathbf{B}_{6}\right)
$$
这样通过$B_0,B_2,B_4,B_6$就会得到中间1,3,5的插帧,或许有人疑惑为什么会有$\mathbf{I'}_{3}$ 和$\hat{\mathbf{I}}_{3}$ ,这两个有什么区别,这里主要就是因为作者做了一个Cycle Consistency的loss,主要是保证中间产生的帧与金字塔最后产生的帧保持空间上的一致性。

 **ConvLSTM**构成的**Inter-Pyramid Recurrent Module**实际上就是为了传递时空上的信息,这里Time Step为2,$B_2^{t}$ 与$B_2^{t+1}$ 实际上是同一张输入,但是进入了两个不同的模块,整体step前进了一步,其中的ConvLSTM就是为了传递C和H的,其公式如下:
$$
\mathbf{H}^{t}, \mathbf{C}^{t}=\mathcal{F}_{\mathrm{c}}\left(\hat{\mathbf{I}}_{3}^{t}, \mathbf{H}^{t-1}, \mathbf{C}^{t-1}\right)
$$
**损失函数非常的简单**,这里不做过多的说明,分为了重构误差$L_p$ **(Pixel Reconstruction)** 和 一致性误差$L_c$ **(Cycle Consistency)** :
$$
\rho(x)=\sqrt{x^{2}+\epsilon^{2}}\\
\mathcal{L}_{p}=\frac{1}{T} \sum_{t=1}^{T} \sum_{n=1}^{2 M-1} \rho\left(\hat{\mathbf{I}}_{n}^{t}-\mathbf{G}_{n}^{t}\right)\\
\mathcal{L}_{c}=\frac{1}{T} \sum_{t=1}^{T} \sum_{n \in \Omega} \rho\left(\mathbf{I}_{n}^{t}-\hat{\mathbf{I}}_{n}^{t}\right)\\
\mathcal{L}=\mathcal{L}_{p}+\mathcal{L}_{c}\\
$$
**数据集**用的是:**Adobe240**和**YouTube240**,可以看到论文的效果取了Scale=4的时候跟GT已经看不出太大的区别了。
**ConvLSTM**构成的**Inter-Pyramid Recurrent Module**实际上就是为了传递时空上的信息,这里Time Step为2,$B_2^{t}$ 与$B_2^{t+1}$ 实际上是同一张输入,但是进入了两个不同的模块,整体step前进了一步,其中的ConvLSTM就是为了传递C和H的,其公式如下:
$$
\mathbf{H}^{t}, \mathbf{C}^{t}=\mathcal{F}_{\mathrm{c}}\left(\hat{\mathbf{I}}_{3}^{t}, \mathbf{H}^{t-1}, \mathbf{C}^{t-1}\right)
$$
**损失函数非常的简单**,这里不做过多的说明,分为了重构误差$L_p$ **(Pixel Reconstruction)** 和 一致性误差$L_c$ **(Cycle Consistency)** :
$$
\rho(x)=\sqrt{x^{2}+\epsilon^{2}}\\
\mathcal{L}_{p}=\frac{1}{T} \sum_{t=1}^{T} \sum_{n=1}^{2 M-1} \rho\left(\hat{\mathbf{I}}_{n}^{t}-\mathbf{G}_{n}^{t}\right)\\
\mathcal{L}_{c}=\frac{1}{T} \sum_{t=1}^{T} \sum_{n \in \Omega} \rho\left(\mathbf{I}_{n}^{t}-\hat{\mathbf{I}}_{n}^{t}\right)\\
\mathcal{L}=\mathcal{L}_{p}+\mathcal{L}_{c}\\
$$
**数据集**用的是:**Adobe240**和**YouTube240**,可以看到论文的效果取了Scale=4的时候跟GT已经看不出太大的区别了。
 而且**Scale越大图片质量就越好**:
而且**Scale越大图片质量就越好**:

加载全部内容