2019 ICCV、CVPR、ICLR之视频预测读书笔记
ManWingloeng 人气:22019 ICCV、CVPR、ICLR之视频预测读书笔记
作者 | 文永亮
学校 | 哈尔滨工业大学(深圳)
研究方向 | 视频预测、时空序列预测
ICCV 2019
CVP

github地址:https://github.com/JudyYe/CVP
这是卡耐基梅隆和facebook的一篇paper,这篇论文的关键在于分解实体预测再组成,我们观察到一个场景是由不同实体经历不同运动组成的,所以这里提出的方法是通过隐式预测独立实体的未来状态,同时推理它们之间的相互作用,并使用预测状态来构成未来的视频帧,从而实现了对实体分解组成的视频预测。
该论文使用了两个数据集,一个是包含可能掉落的堆叠物体ShapeStacks,另一个包含人类在体育馆中进行活动的视频Penn Action,并表明论文的方法可以在这些不同的环境中进行逼真的随机视频预测。

主要架构有下面三个部分组成:
Entity Predictor(实体预测模块): 预测每一个实体表示的未来状态
Frame Decoder(帧解码器): 从实体表示中解码成frame
Encoder(编码器): 把frame编码成u作为LSTM的cell-state得到输出记录时序信息\(z^1...z^t\)
(最后其实就是concat进去,见如下::)
obj_vecs = torch.cat([pose, bbox, diff_z], dim=-1)
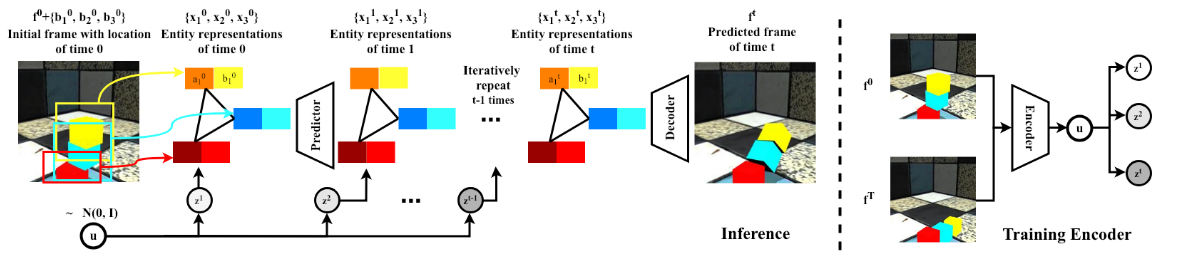
模型将具有已知或者检测到的实体位置的图像作为输入。每个实体均表示为其位置和隐式特征。每个实体的表示为\({x_n^t}^N_{n=1}\equiv\{(b_n^t,a^t_n)\}^N_{n=1}\), \(b_n^t\)表示为预测的位置,\(a^t_n\)表示为隐式特征,这样的分解方便我们高效地预测每一个实体的未来状态,给定当前实体表示形式和采样的潜在变量,我们的预测模块将在下一个时间步预测这些表示形式。我们所学的解码器将预测的表示组合为代表预测的未来的图像。在训练期间,使用潜在编码器模块使用初始帧和最终帧来推断潜在变量的分布。
分解的思想一般都用mask来体现,就是把变化的与不变的用掩码表示后在组合起来,预测变化的部分,这是分而治之的思想。
让\(\left\{\left(\bar{\phi}_{n}, \bar{M}_{n}\right)=g\left(a_{n}\right)\right\}_{n=1}^{N}\)表示在g的网络结构下解码每一个实体的特征和空间掩码,让\(\mathcal{W}\)表示类似Spatial Transformer Networks的空间变化网络,可以得到下面的实体的特征和掩码\(\phi_{n}\)和\(M_n\).
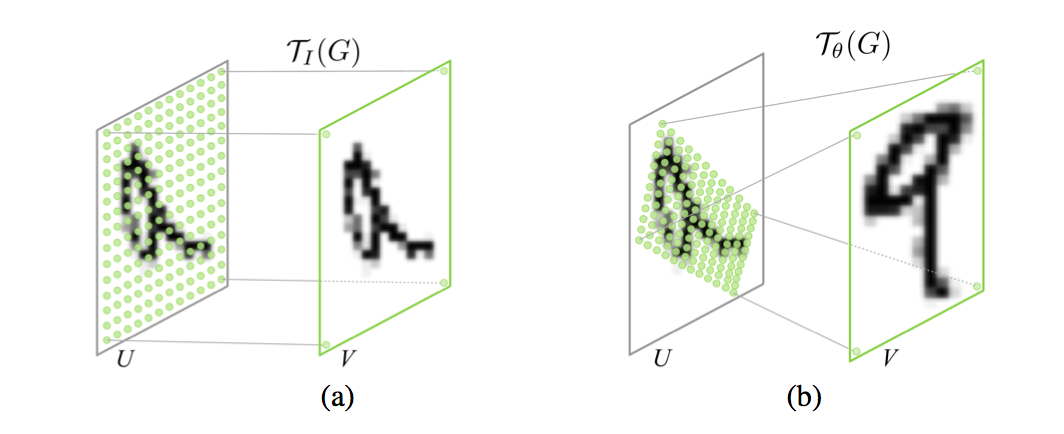
\[
\phi_{n}=\mathcal{W}\left(\bar{\phi}_{n}, b_{n}\right) ; \quad M_{n}=\mathcal{W}\left(\bar{M}_{n}, b_{n}\right)
\]
通过权重掩码和各个特征的结合最后取平均,这样我们就得到图像级别的特征,即每一帧的特征,\(M_{bg}\)是常数的空间掩码(论文取值为0.1),其组成的特征表示如下:
\[
\phi=\frac{\phi_{b g} \odot M_{b g} {\oplus \sum_{n} \phi_{n} \odot M_{n}}}{M_{b g}\oplus\sum_{n} M_{n}}
\]
上面的公式很好理解,\(\odot\)是像素乘法,\(\oplus\)是像素加法,\(\phi_{b g} \odot M_{b g} {\oplus \sum_{n} \phi_{n} \odot M_{n}}\)这个是加权后的背景特征与加权后的每个实体的特征的总和,最后除以权重和。这样就得到了解码的结果。
编码器的作用是把各帧\(f^0...f^T\)编码成u,u的分布服从标准正态分布\(\mathcal{N}(0, I)\),所以需要拉近两者之间的KL散度,u作为cell-state输入LSTM得到{\(z_t\)}表示时间序列的隐状态。
\[
L_{e n c}=K L[q(u) \| \mathcal{N}(0, I)]
\]
解码损失就是实体表示\(\hat{x}_{n}^{t}\)经过解码与真实图像\(\hat{f}^{t}\)的L1损失。
\[
L_{d e c}=\sum_{t=0}^{T}\left\|\mathcal{D}\left(\left\{\hat{x}_{n}^{t}\right\}, f^{0}\right)-\hat{f}^{t}\right\|_{1}
\]
预测损失即为解码损失加上位置损失\[\sum_{n=1}^{N}\left\|b_{n}^{t}-\hat{b}_{n}^{t}\right\|^{2}\].
\[
L_{p r e d}=\sum_{t=1}^{T}\left(\left\|\mathcal{D}\left(\left\{x_{n}^{t}\right\}, f^{0}\right)-\hat{f}^{t}\right\|_{1}+\lambda_{1} \sum_{n=1}^{N}\left\|b_{n}^{t}-\hat{b}_{n}^{t}\right\|^{2}\right)
\]
其总的损失函数即三个损失的和。
\[
L=L_{d e c}+L_{p r e d}+\lambda_{2} L_{e n c}
\]
Non-Local ConvLSTM

github地址:https://github.com/xyiyy/NL-ConvLSTM (Code will be published later)
Non-Local ConvLSTM是复旦大学和b站的论文,其实这篇不太算视频预测方向,这是使用了在ConvLSTM中使用Non-Local结合前一帧增强图像减少视频压缩的伪影,是视频压缩的领域,但是对我有些启发,Non-Local最初就是用于视频分类的。
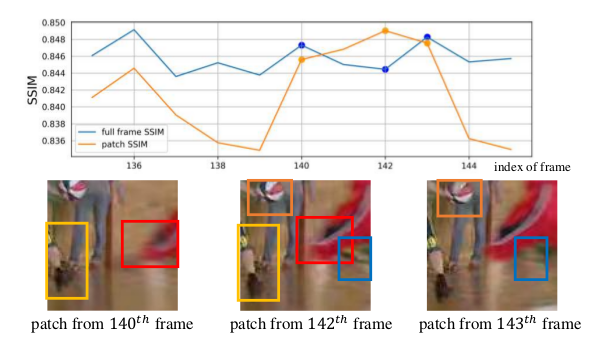
SSIM是用来评价整张图的质量,但是对于一张质量不好的图来说他的patch并不一定差,对于一张好图来说他的patch也不一定好,所以作者用Non-Local来捕捉两帧之间特征图间像素的相似性。
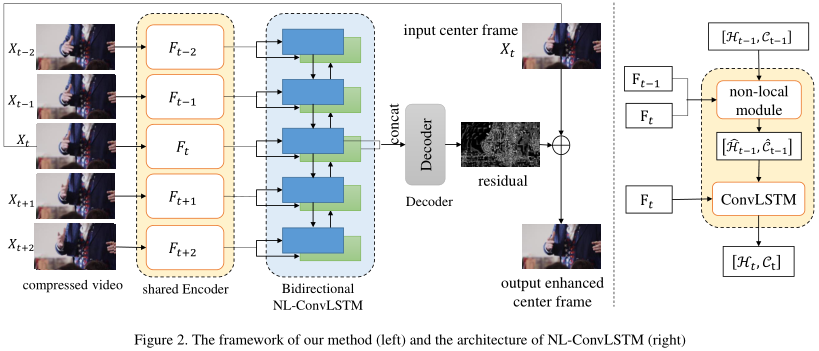
ConvLSTM可以表示成下面的公式:
\[
\left[\mathcal{H}_{t}, \mathcal{C}_{t}\right]=\operatorname{Conv} L S T M\left(F_{t},\left[\mathcal{H}_{t-1}, \mathcal{C}_{t-1}\right]\right)
\]
即hidden state (\(H_t,C_t\)) 是从上一次的hidden state (\(H_{t_1},C_{t-1}\)) 和\(F_t\) 经过ConvLSTM-cell得到的。
而NL-ConvLSTM是在ConvLSTM的基础上加了Non-local的方法,可以表示如下:
\[
\begin{aligned} S_{t} &=N L\left(F_{t-1}, F_{t}\right) \\\left[\hat{\mathcal{H}}_{t-1}, \hat{\mathcal{C}}_{t-1}\right] &=N L W \operatorname{arp}\left(\left[\mathcal{H}_{t-1}, \mathcal{C}_{t-1}\right], S_{t}\right) \\\left[H_{t}, C_{t}\right] &=\operatorname{Conv} L S T M\left(F_{t},\left[\hat{\mathcal{H}}_{t-1}, \hat{c}_{t-1}\right]\right) \end{aligned}
\]
其中\(S_{t} \in \mathbb{R}^{N \times N}\)是当前帧\(F_t\) 与前一帧的\(F_{t-1}\) 的相似矩阵,这里的Non-Local的操作是一种特殊的attention,这不是self-attention,是比较前一帧获得相似矩阵再计算attention,NLWrap操作可以用数学表达如下:
\[
\begin{aligned} D_{t}(i, j) &=\left\|F_{t-1}(i)-F_{t}(j)\right\|_{2} \\ S_{t}(i, j) &=\frac{\exp \left(-D_{t}(i, j) / \beta\right)}{\sum_{\forall i} \exp \left(-D_{t}(i, j) / \beta\right)} \\\left[\hat{\mathcal{H}}_{t-1}, \hat{\mathcal{C}}_{t-1}\right] &=\left[\mathcal{H}_{t} \cdot S_{t}, \mathcal{C}_{t} \cdot S_{t}\right] \end{aligned}
\]
这里的公式估计论文写错了,我认为是:
\[
\left[\hat{\mathcal{H}}_{t-1}, \hat{\mathcal{C}}_{t-1}\right] =\left[\mathcal{H}_{t-1} \cdot S_{t}, \mathcal{C}_{t-1} \cdot S_{t}\right]
\]
但是由于Non-local计算量太大,作者提出了两阶段的Non-Local相似度估计,即池化之后做相似度计算如下:
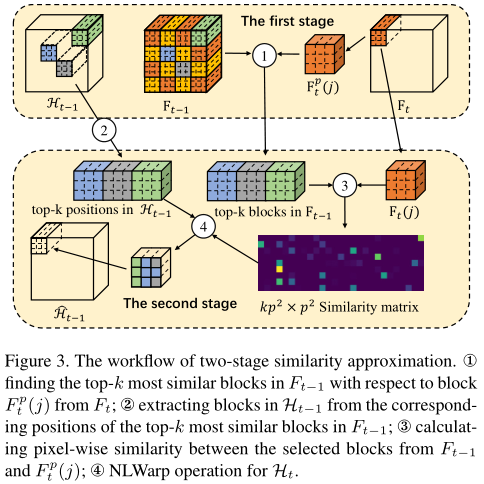
ICLR 2019
SAVP

github地址:https://github.com/alexlee-gk/video_prediction
当我们与环境中的对象进行交互时,我们可以轻松地想象我们的行为所产生的后果:推一颗球,它会滚走;扔一个花瓶,它会碎掉。视频预测中的主要挑战是问题的模棱两可,未来的发展方向似乎有太多。就像函数的导数能够预测该值附近的走向,当我们预测非常接近的未来时我们能够未来可期,可是当可能性的空间超出了几帧之后,并且该问题本质上变成了多模的,即预测就变得更多样了。


这篇把GAN和VAE都用在了视频预测里,其实GAN-VAE在生成方面早有人结合,只是在视频预测中没有人提出,其实提出的SAVP是SV2P (Stochastic Variational Video Prediction) 和SVG-LP (Stochastic Video Generation with a Learned Prior) 的结合。
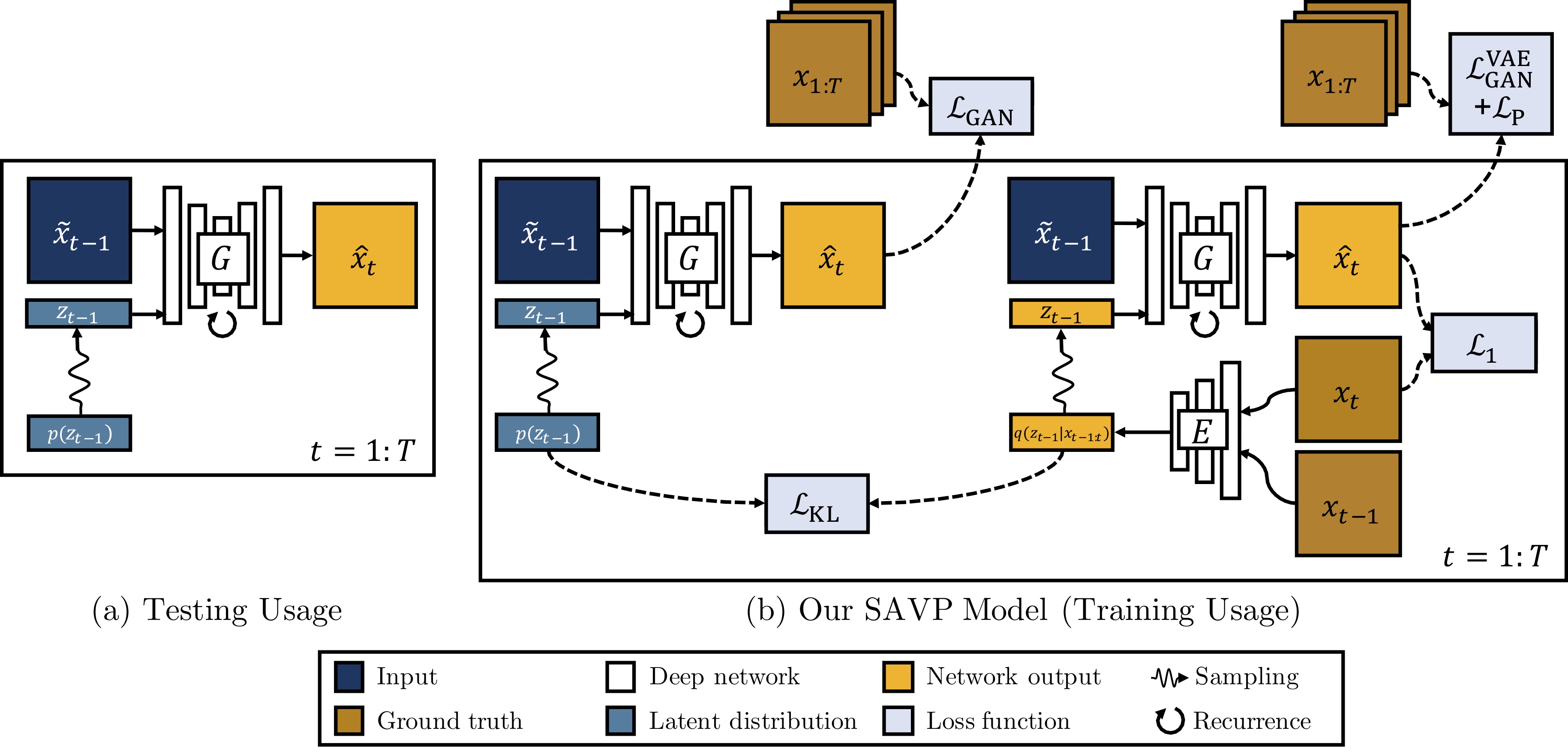
在训练期间,隐变量从\(q(z_{t-1}|x_{t-1:t})\)中采样,对每一帧的生成都可以看作是对\(\hat{x}_{t}\)的重构,\(x_t\)与\({x}_{t-1}\)被Encoder编码为隐变量\(z_{t-1}\),前一帧\(x_{t-1}\)与隐变量\(z_{t-1}\)经过G模型之后得到预测帧\(\hat{x}_t\)要计算与当前帧\(x_t\)的\(L_1\)损失,使其生成要尽量相似。
\[
\mathcal{L}_{1}(G, E)=\mathbb{E}_{\mathbf{x}_{0: T}\left.\mathbf{z}_{t} \sim E\left(\mathbf{x}_{t: t+1}\right)\right|_{t=0} ^{T-1}}{\left[\sum_{t=1}^{T}\left\|\mathbf{x}_{t}-G\left(\mathbf{x}_{t-1}, \mathbf{z}_{t-1}\right)\right\|_{1}\right]}.
\]
在测试阶段我们的隐变量从先验分布\(p(z_{t-1})\)直接采样,\(z_{t-1}\)与\(\tilde{x}_{t-1}\) 经过G生成下一帧的预测图\(\hat{x}_t\) ,所以需要同时拉近\(q(z_{t-1}|x_{t-1:t})\)与\(p(z_{t-1})\)的分布,其KL散度如下:
\[
\mathcal{L}_{\mathrm{KL}}(E)=\mathbb{E}_{\mathbf{x}_{0: T}}\left[\sum_{t=1}^{T} \mathcal{D}_{\mathrm{KL}}\left(E\left(\mathbf{x}_{t-1: t}\right) \| p\left(\mathbf{z}_{t-1}\right)\right)\right]
\]
所以G和E的目标函数如下:
\[
G^{*}, E^{*}=\arg \min _{G, E} \lambda_{1} \mathcal{L}_{1}(G, E)+\lambda_{\mathrm{KL}} \mathcal{L}_{\mathrm{KL}}(E)
\]
\(L_1\)损失并不是很能反映图像的相似度,既然文章是VAE和GAN的结合,所以在下面提出了判别器去评判图片质量。论文指出单纯的VAE更容易产生模糊图,这里加入的判别器是能够分辨出生成视频序列\(\hat{x}_{1:T}\)与真实视频序列\(x_{1:T}\),这里是比较意想不到的地方,因为这里没有使用直接的图像判别器,而是判别生成序列与真实序列,其D判别器的网络结构是使用了3D卷积基于SNGAN的,G生成器是使用了convLSTM捕捉时空序列信息。
\[
\mathcal{L}_{\mathrm{GAN}}(G, D)=\mathbb{E}_{\mathbf{x}_{1: T}}\left[\log D\left(\mathbf{x}_{1: T}\right)\right]+\mathbb{E}_{\left.\mathbf{x}_{1: T}, \mathbf{z}_{t} \sim p\left(\mathbf{z}_{t}\right)\right)_{t=0}^{T-1}}\left[\log \left(1-D\left(G\left(\mathbf{x}_{0}, \mathbf{z}_{0: T-1}\right)\right)\right)\right]
\]
最后总的损失函数如下:
\[
G^{*}, E^{*}=\arg \min _{G, E} \max _{D, D^{\mathrm{ME}}} \lambda_{1} \mathcal{L}_{1}(G, E)+\lambda_{\mathrm{KL}} \mathcal{L}_{\mathrm{KL}}(E)+\mathcal{L}_{\mathrm{GAN}}(G, D)+\mathcal{L}_{\mathrm{GAN}}^{\mathrm{VAE}}\left(G, E, D^{\mathrm{VAE}}\right)
\]
下面是论文中的实验结果:


CVPR 2019
MIM

github地址:https://github.com/Yunbo426/MIM
这是清华大学的一篇paper,作者Yunbo Wang也是Eidetic 3D LSTM,PredRNN++,PredRNN的作者,自然时空序列的发生过程常常是非平稳( Non-Stationarity )的,在低级的非平稳体现在像素之间的空间相关性或时序性,在高层语义特征的变化其实体现在降水预报中雷达回波的积累,形变或耗散。
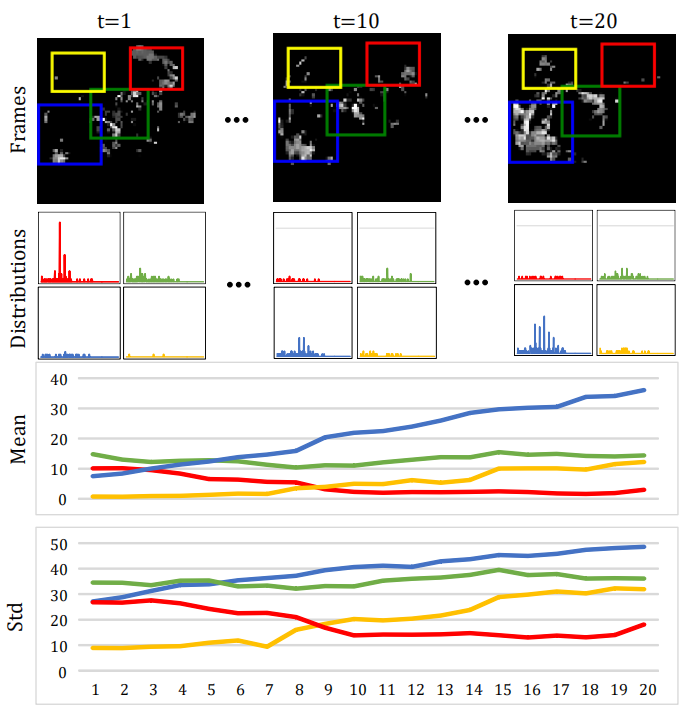
上图是连续20帧雷达图变化,其中白色像素表示降水概率较高。第二、第三、最后一行:通过不同颜色的边框表明相应局部区域的像素值分布、均值和标准差的变化。蓝色和黄色框表明着生成的非平稳变化过程,红色框表明了消散的过程,绿色框为形变过程。
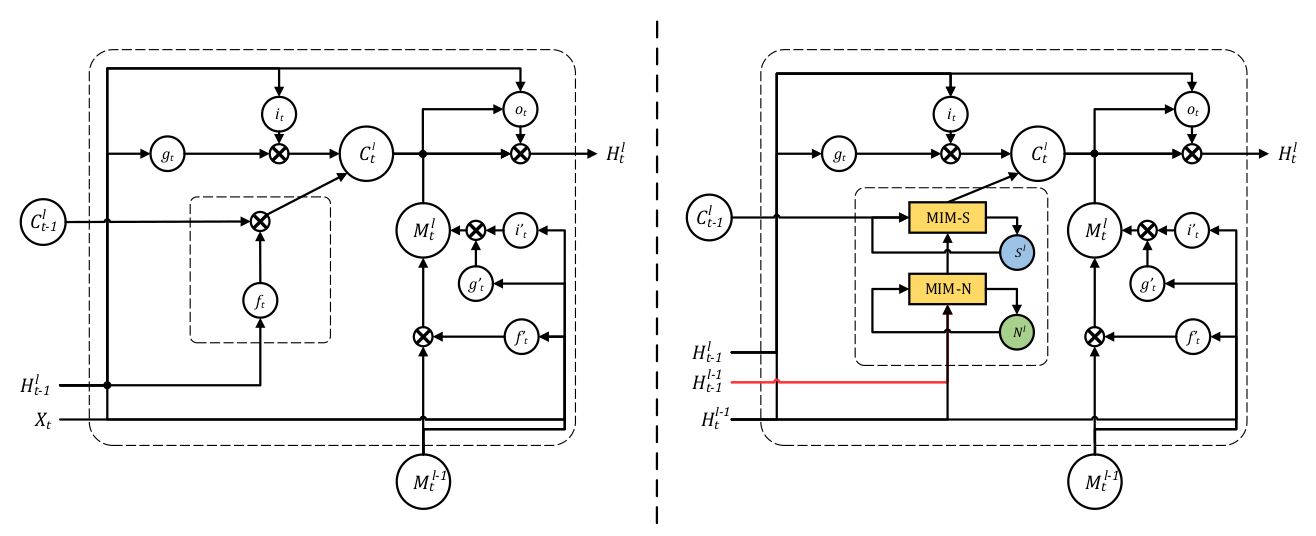
这篇论文的主要工作就是构造了MIM模块代替遗忘门,其中这个模块分为两部分:MIM-N(非平稳模块),MIM-S(平稳模块)。
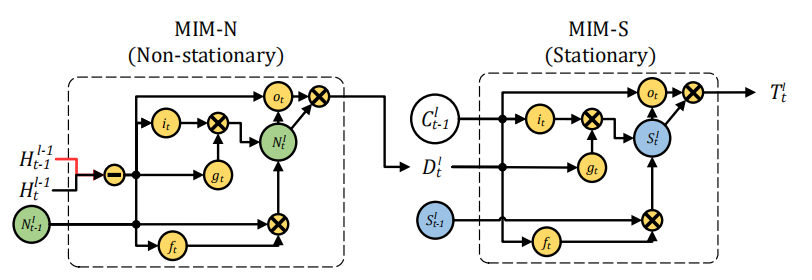
MIM-N所有的门\(g_t\),\(i_t\), \(f_t\) ,和\(o_t\)都用\(\left(\mathcal{H}_{t}^{l-1}-\mathcal{H}_{t-1}^{l-1}\right)\) 短期记忆的隐状态的帧差更新,因为这样强调了非平稳变换,最后得到特征差\(D_t^l\)和\(C^l_{t-1}\)作为MIM-S输入,MIM-S会根据原记忆\(C^l_{t-1}\)和特征差\(D_t^l\)决定变化多少,如果\(D_t^l\) 很小,意味着并不是非平稳变化,即变化得平稳,MIM-S很大程度会继续沿用\(C^l_{t-1}\);如果\(D_t^l\) 很大,则会重写记忆并且更关注于非平稳变化。
其数学表达式如下:
- MIM-N:
\[ \begin{array}{l}{g_{t}=\tanh \left(W_{x g} *\left(\mathcal{H}_{t}^{l-1}-\mathcal{H}_{t-1}^{l-1}\right)+W_{n g} * \mathcal{N}_{t-1}^{l}+b_{g}\right.} \\ {i_{t}=\sigma\left(W_{x i} *\left(\mathcal{H}_{t}^{l-1}-\mathcal{H}_{t-1}^{l-1}\right)+W_{n i} * \mathcal{N}_{t-1}^{l}+b_{i}\right)} \\ {f_{t}=\sigma\left(W_{x f} *\left(\mathcal{H}_{t}^{l-1}-\mathcal{H}_{t-1}^{l-1}\right)+W_{n f} * \mathcal{N}_{t-1}^{l}+b_{f}\right)} \\ {\mathcal{N}_{t}^{l}=f_{t} \odot \mathcal{N}_{t-1}^{l}+i_{t} \odot g_{t}} \\ {o_{t}=\sigma\left(W_{x o} *\left(\mathcal{H}_{t}^{l-1}-\mathcal{H}_{t-1}^{l-1}\right)+W_{n o} * \mathcal{N}_{t}^{l}+b_{o}\right)} \\ {\mathcal{D}_{t}^{l}=\operatorname{MIM-N}\left(\mathcal{H}_{t}^{l-1}, \mathcal{H}_{t-1}^{l-1}, \mathcal{N}_{t-1}^{l}\right)=o_{t} \odot \tanh \left(\mathcal{N}_{t}^{l}\right)}\end{array} \]
MIM-S:
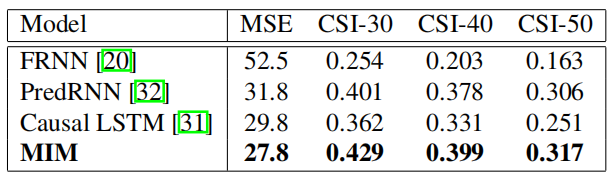
\[ \begin{array}{l}{g_{t}=\tanh \left(W_{d g} * \mathcal{D}_{t}^{l}+W_{c g} * \mathcal{C}_{t-1}^{l}+b_{g}\right)} \\ {i_{t}=\sigma\left(W_{d i} * \mathcal{D}_{t}^{l}+W_{c i} * \mathcal{C}_{t-1}^{l}+b_{i}\right)} \\ {f_{t}=\sigma\left(W_{d f} * \mathcal{D}_{t}^{l}+W_{c f} * \mathcal{C}_{t-1}^{l}+b_{f}\right)} \\ {S_{t}^{l}=f_{t} \odot \mathcal{S}_{t-1}^{l}+i_{t} \odot g_{t}} \\ {o_{t}=\sigma\left(W_{d o} * \mathcal{D}_{t}^{l}+W_{c o} * \mathcal{C}_{t-1}^{l}+W_{s o} * S_{t}^{l}+b_{o}\right)} \\ {\mathcal{T}_{t}^{l}=\operatorname{MIM-S}\left(\mathcal{D}_{t}^{l}, \mathcal{C}_{t-1}^{l}, \mathcal{S}_{t-1}^{l}\right)=o_{t} \odot \tanh \left(\mathcal{S}_{t}^{l}\right)}\end{array} \]这一篇的实验做的很全面,其效果如下,均达到了state-of-the-art:
Moving Mnist:
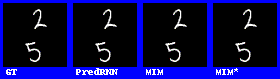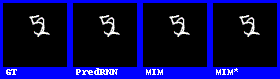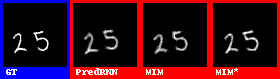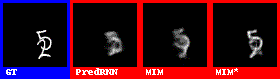
在数字集上的表现效果较好。
Radar Echo:

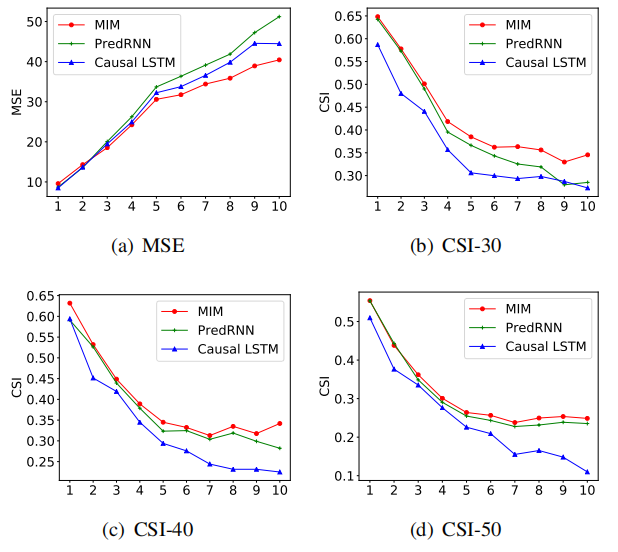
其实可以看到MSE在预测第五帧才有明显的优势,CSI-40和CSI-50其实并没有明显优势。
总结
视频预测是结合了时空序列信息的预测,其关键在于如何利用时序信息,ConvLSTM就是把卷积直接与LSTM结合记录时序信息,而在VAE相关的模型中时间序列被编码成隐变量拼接起来。除了修改LSTM-cell的结构(e.g. MIM)或者其他的网络结构尝试捕捉其他信息,我们常见的一种思想就是分而治之,把变与不变用掩码区分出来,有点像我之前解读的一篇BANet,这里的CVP方法甚至对实体直接进行预测,这些都是比较好的想法。
加载全部内容