Algorithm: 多项式乘法 Polynomial Multiplication: 快速傅里叶变换 FFT / 快速数论变换 NTT
BrianPeng 人气:1Intro:
本篇博客将会从朴素乘法讲起,经过分治乘法,到达FFT和NTT
旨在能够让读者(也让自己)充分理解其思想
模板题入口:洛谷 P3803 【模板】多项式乘法(FFT)
朴素乘法
约定:两个多项式为\(A(x)=\sum_{i=0}^{n}a_ix^i,B(x)=\sum_{i=0}^{m}b_ix^i\)
Prerequisite knowledge:
初中数学知识(手动滑稽)
最简单的多项式方法就是逐项相乘再合并同类项,写成公式:
若\(C(x)=A(x)B(x)\),那么\(C(x)=\sum_{i=0}^{n+m}c_ix^i\),其中\(c_i=\sum_{j=0}^ia_jb_{i-j}\)
于是一个朴素乘法就产生了,见代码(利用某种丧心病狂的方式省了\(b\)数组)
//This program is written by Brian Peng.
#pragma GCC optimize("Ofast","inline","no-stack-protector")
#include<bits/stdc++.h>
using namespace std;
#define Rd(a) (a=read())
#define Gc(a) (a=getchar())
#define Pc(a) putchar(a)
int read(){
register int x;register char c(getchar());register bool k;
while(!isdigit(c)&&c^'-')if(Gc(c)==EOF)exit(0);
if(c^'-')k=1,x=c&15;else k=x=0;
while(isdigit(Gc(c)))x=(x<<1)+(x<<3)+(c&15);
return k?x:-x;
}
void wr(register int a){
if(a<0)Pc('-'),a=-a;
if(a<=9)Pc(a|'0');
else wr(a/10),Pc((a%10)|'0');
}
signed const INF(0x3f3f3f3f),NINF(0xc3c3c3c3);
long long const LINF(0x3f3f3f3f3f3f3f3fLL),LNINF(0xc3c3c3c3c3c3c3c3LL);
#define Ps Pc(' ')
#define Pe Pc('\n')
#define Frn0(i,a,b) for(register int i(a);i<(b);++i)
#define Frn1(i,a,b) for(register int i(a);i<=(b);++i)
#define Frn_(i,a,b) for(register int i(a);i>=(b);--i)
#define Mst(a,b) memset(a,b,sizeof(a))
#define File(a) freopen(a".in","r",stdin),freopen(a".out","w",stdout)
#define N (2000010)
int n,m,a[N],b,c[N];
signed main(){
Rd(n),Rd(m);
Frn1(i,0,n)Rd(a[i]);
Frn1(i,0,m){Rd(b);Frn1(j,0,n)c[i+j]+=b*a[j];}
Frn1(i,0,n+m)wr(c[i]),Ps;
exit(0);
}Time complexity: \(O(nm)\),如果\(m=O(n)\),则为\(O(n^2)\)
Memory complexity: \(O(n)\)
看看效果

意料之中
朴素分治乘法
P.s 这一部分讲述了FFT的分治方法,与FFT还是有区别的,如果已经理解的可以跳过
约定:\(n\)为同时属于\(A(x),B(x)\)次数界的最小的\(2\)的正整数幂,并将两个多项式设为\(A(x)=\sum_{i=0}^{n-1}a_ix^i,B(x)=\sum_{i=0}^{n-1}b_ix^i\),不存在的系数补零
次数界:严格\(>\)一个多项式次数的整数(E.g 多项式\(P(x)=x^2+x+1\)的次数界为\(\geqslant3\)的所有整数)
Reference:
《算法导论》
Prerequisite knowledge:
分治思想
现在来考虑如何去优化乘法
尝试将两个多项式按照未知项次数的奇偶性分开:
\(A(x)=A^{[0]}(x^2)+xA^{[1]}(x^2),B(x)=B^{[0]}(x^2)+xB^{[1]}(x^2)\)
其中\(A^{[0]}(x)=\sum_{i=0}^{n/2-1}a_{2i}x^i,A^{[1]}(x)=\sum_{i=0}^{n/2-1}a_{2i+1}x^i\),\(B^{[0]}(x)\)与\(B^{[1]}(x)\)同理
于是两个多项式就被拆成了两个次数界为\(n/2\)的四个多项式啦:
P.s 以下的公式中,用\(A\)表示\(A(x)\),\(A^{[0]}\)和\(A^{[1]}\)分别表示\(A^{[0]}(x^2)\)和\(A^{[1]}(x^2)\),\(B\)同理
\(AB=(A^{[0]}+xA^{[1]})(B^{[0]}+xB^{[1]})=A^{[0]}B^{[0]}+x(A^{[1]}B^{[0]}+A^{[0]}B^{[1]})+x^2A^{[1]}B^{[1]}\)
在此可以发现一种分治算法:把两个多项式折半,然后再递归算\(4\)次多项式乘法,最后合并加起来(反正多项式加法是\(O(n)\)的)
P.s 注意合并方式:\(A^{[0]}\)和\(A^{[1]}\)分别表示\(A^{[0]}(x^2)\)和\(A^{[1]}(x^2)\),所以是交错的,见代码
(为了省空间用了vector)
//This program is written by Brian Peng.
#pragma GCC optimize("Ofast","inline","no-stack-protector")
#include<bits/stdc++.h>
using namespace std;
#define Rd(a) (a=read())
#define Gc(a) (a=getchar())
#define Pc(a) putchar(a)
int read(){
register int x;register char c(getchar());register bool k;
while(!isdigit(c)&&c^'-')if(Gc(c)==EOF)exit(0);
if(c^'-')k=1,x=c&15;else k=x=0;
while(isdigit(Gc(c)))x=(x<<1)+(x<<3)+(c&15);
return k?x:-x;
}
void wr(register int a){
if(a<0)Pc('-'),a=-a;
if(a<=9)Pc(a|'0');
else wr(a/10),Pc((a%10)|'0');
}
signed const INF(0x3f3f3f3f),NINF(0xc3c3c3c3);
long long const LINF(0x3f3f3f3f3f3f3f3fLL),LNINF(0xc3c3c3c3c3c3c3c3LL);
#define Ps Pc(' ')
#define Pe Pc('\n')
#define Frn0(i,a,b) for(register int i(a);i<(b);++i)
#define Frn1(i,a,b) for(register int i(a);i<=(b);++i)
#define Frn_(i,a,b) for(register int i(a);i>=(b);--i)
#define Mst(a,b) memset(a,b,sizeof(a))
#define File(a) freopen(a".in","r",stdin),freopen(a".out","w",stdout)
typedef vector<int> Vct;
int n,m,s;
Vct a,b,c;
void add(Vct&a,Vct&b,Vct&c){Frn0(i,0,c.size())c[i]=a[i]+b[i];}
void mlt(Vct&a,Vct&b,Vct&c,int n);
signed main(){
Rd(n),Rd(m),a.resize(s=1<<int(log2(max(n,m))+1)),b.resize(s),c.resize(s<<1);
Frn1(i,0,n)Rd(a[i]);
Frn1(i,0,m)Rd(b[i]);
mlt(a,b,c,s);
Frn1(i,0,n+m)wr(c[i]),Ps;
exit(0);
}
void mlt(Vct&a,Vct&b,Vct&c,int n){
int n2(n>>1);
Vct a0(n2),a1(n2),b0(n2),b1(n2),ab0(n),ab1(n),abm(n);
if(n==1){c[0]=a[0]*b[0];return;}
Frn0(i,0,n2)a0[i]=a[i<<1],a1[i]=a[i<<1|1],b0[i]=b[i<<1],b1[i]=b[i<<1|1];
mlt(a0,b0,ab0,n2),mlt(a1,b1,ab1,n2);
Frn0(i,0,n)c[i<<1]=ab0[i]+(i?ab1[i-1]:0);
mlt(a0,b1,ab0,n2),mlt(a1,b0,ab1,n2),add(ab0,ab1,abm);
Frn0(i,0,n-1)c[i<<1|1]=abm[i];
}看看效果
好像更惨……
为什么呢,因为这个算法的时间复杂度还是\(O(n^2)\)的,具体证明如下
\(T(n)=4T(n/2)+f(n)\),其中\(f(n)=O(n)\)(就是\(n\)位加法的时间)
运用主方法,\(a=4,b=2,log_ba=log_2 4=2>1\),所以\(T(n)=O(n^{log_ba})=O(n^2)\)
而且不仅复杂度高,常数因子也因为递归变高了
所以继续优化吧……
分治乘法
接上上一部分的内容,考虑如何优化时间复杂度
先来一个小插曲:如何只做\(3\)次乘法,求出线性多项式\(ax+b\)与\(cx+d\)的乘积
先看看结果:\((ax+b)(cx+d)=acx^2+(ad+bc)x+bd\),总共有\(4\)次乘法
所以如果只用\(3\)次乘法,那么\(ad+bc\)必须只能用一次乘法得到
尝试把\(3\)个系数加起来,就是\(ac+ad+bc+bd=(a+b)(c+d)\)
答案出来了,用\(3\)次乘法分别算出\(ac,bd\)与\((a+b)(c+d)\),那么中间项系数\(=(a+b)(c+d)-ac-bd\)
回到原题目
\(AB=(A^{[0]}+xA^{[1]})(B^{[0]}+xB^{[1]})=A^{[0]}B^{[0]}+x(A^{[1]}B^{[0]}+A^{[0]}B^{[1]})+x^2A^{[1]}B^{[1]}\)
于是中间项也可以使用类似的方法:\(A^{[1]}B^{[0]}+A^{[0]}B^{[1]}=(A^{[0]}+A^{[1]})(B^{[0]}+B^{[1]})-A^{[0]}B^{[0]}-A^{[1]}B^{[1]}\)
成功减少一次乘法运算,见代码
//This program is written by Brian Peng.
#pragma GCC optimize("Ofast","inline","no-stack-protector")
#include<bits/stdc++.h>
using namespace std;
#define Rd(a) (a=read())
#define Gc(a) (a=getchar())
#define Pc(a) putchar(a)
int read(){
register int x;register char c(getchar());register bool k;
while(!isdigit(c)&&c^'-')if(Gc(c)==EOF)exit(0);
if(c^'-')k=1,x=c&15;else k=x=0;
while(isdigit(Gc(c)))x=(x<<1)+(x<<3)+(c&15);
return k?x:-x;
}
void wr(register int a){
if(a<0)Pc('-'),a=-a;
if(a<=9)Pc(a|'0');
else wr(a/10),Pc((a%10)|'0');
}
signed const INF(0x3f3f3f3f),NINF(0xc3c3c3c3);
long long const LINF(0x3f3f3f3f3f3f3f3fLL),LNINF(0xc3c3c3c3c3c3c3c3LL);
#define Ps Pc(' ')
#define Pe Pc('\n')
#define Frn0(i,a,b) for(register int i(a);i<(b);++i)
#define Frn1(i,a,b) for(register int i(a);i<=(b);++i)
#define Frn_(i,a,b) for(register int i(a);i>=(b);--i)
#define Mst(a,b) memset(a,b,sizeof(a))
#define File(a) freopen(a".in","r",stdin),freopen(a".out","w",stdout)
typedef vector<int> Vct;
int n,m,s;
Vct a,b,c;
void add(Vct&a,Vct&b,Vct&c){Frn0(i,0,c.size())c[i]=a[i]+b[i];}
void mns(Vct&a,Vct&b,Vct&c){Frn0(i,0,c.size())c[i]=a[i]-b[i];}
void mlt(Vct&a,Vct&b,Vct&c);
signed main(){
Rd(n),Rd(m),a.resize(s=1<<int(log2(max(n,m))+1)),b.resize(s),c.resize(s<<1);
Frn1(i,0,n)Rd(a[i]);
Frn1(i,0,m)Rd(b[i]);
mlt(a,b,c);
Frn1(i,0,n+m)wr(c[i]),Ps;
exit(0);
}
void mlt(Vct&a,Vct&b,Vct&c){
int n(a.size()),n2(a.size()>>1);
Vct a0(n2),a1(n2),b0(n2),b1(n2),ab0(n),ab1(n),abm(n);
if(n==1){c[0]=a[0]*b[0];return;}
Frn0(i,0,n2)a0[i]=a[i<<1],a1[i]=a[i<<1|1],b0[i]=b[i<<1],b1[i]=b[i<<1|1];
mlt(a0,b0,ab0),mlt(a1,b1,ab1);
Frn0(i,0,n)c[i<<1]=ab0[i]+(i?ab1[i-1]:0);
add(a0,a1,a0),add(b0,b1,b0),mlt(a0,b0,abm),mns(abm,ab0,abm),mns(abm,ab1,abm);
Frn0(i,0,n-1)c[i<<1|1]=abm[i];
}看看效果

比朴素分治乘法好一点,但是还是没朴素乘法强,还是很惨
看看这个算法的时间复杂度:
\(T(n)=3T(n/2)+f(n)\),其中\(f(n)=O(n)\)
运用主方法,\(a=3,b=2,\log_ba=\log_2 3\approx1.58>1\),所以\(T(n)=O(n^{\log_ba})=O(n^{\log_2 3})\)
额那不是应该比朴素算法要好吗,这是什么情况
Reason 1. 分治乘法的常数因子太大
Reason 2. 打开\(\#5\)数据一看,\(n=1,m=3e6\),那么\(O(n^{\log_2 3})\)的分治乘法也顶不过\(O(nm)\)的朴素乘法啊……
所以就要请上本文的主角了
快速傅里叶变换 FFT (Fast Fourier Transform)
Fairly Frightening Transform
约定:\(n\)为属于\(A(x),B(x)\)的乘积\(C(x)\)次数界的最小的\(2\)的正整数幂(即满足\(>\)输入\(n+m\)的最小的\(2\)的正整数幂),并同样将两个多项式设为\(A(x)=\sum_{i=0}^{n-1}a_ix^i,B(x)=\sum_{i=0}^{n-1}b_ix^i\)
Reference:
《算法导论》
自为风月马前卒:快速傅里叶变换(FFT)详解
Prerequisite knowledge:
分治思想
复数的基本知识
线性代数的基本知识
Part 1: 多项式的两种表示方式
1. 系数表达
对一个次数界为\(n\)的多项式\(A(x)=\sum_{i=0}^{n-1}a_ix^i\),其系数表达是向量\(\pmb{a}=\left[\begin{matrix}a_0\\a_1\\\vdots\\a_{n-1}\end{matrix} \right]\)
使用系数表达时,下列操作的时间复杂度:
求值\(O(n)\)
加法\(O(n)\)
乘法朴素\(O(n^2)\),优化\((n^{\log_2 3})\)(即分治乘法)
P.s 当多项式\(C(x)=A(x)B(x)\)时,\(\pmb{c}\)被称为\(\pmb{a}\)与\(\pmb{b}\)的卷积(convolution),记为\(\pmb{c}=\pmb{a}\bigotimes\pmb{b}\)
2. 点值表达
一个次数界为\(n\)的多项式\(A(x)\)的点值表达是一个有\(n\)个点值对所组成的集合\(\{(x_0,y_0),(x_1,y_1),\cdots,(x_{n-1},y_{n-1})\}\)
进行\(n\)次求值就可以把系数表达转化为点值表达,总时间\(O(n^2)\),用公式表示就是:
\(\left[\begin{matrix}1&x_0&x_0^2&\cdots&x_0^{n-1}\\1&x_1&x_1^2&\cdots&x_1^{n-1}\\\vdots&\vdots&\vdots&\ddots&\vdots\\1&x_{n-1}&x_{n-1}^2&\cdots&x_{n-1}^{n-1}\end{matrix} \right]\left[\begin{matrix}a_0\\a_1\\\vdots\\a_{n-1}\end{matrix} \right]=\left[\begin{matrix}y_0\\y_1\\\vdots\\y_{n-1}\end{matrix} \right]\)
其中左边的矩阵表示为\(V(x_0,x_1,\cdots,x_{n-1})\)称为范德蒙德矩阵,于是可以将公式简化为\(V(x_0,x_1,\cdots,x_{n-1})\pmb{a}=\pmb{y}\)
使用拉格朗日公式,可以在\(O(n^2)\)时间将点值表达转化为系数表达,该过程称为插值
对于两个在相同位置求值的点值表达多项式,下列操作的时间复杂度:
加法\(O(n)\)(只要将各个位置的\(y\)值相加即可)
乘法\(O(n)\)(同理)
所以这就是使用FFT的原因:通过精心选取\(x\)值,可以在\(O(n\log n)\)时间完成求值,再\(O(n)\)乘法,最后\(O(n\log n)\)插值
傅里叶大神究竟选了什么神奇的\(x\)值呢,请看
Part 2: 单位复数根及其性质
\(n\)次单位复数根是满足\(\omega^n=1\)的复数\(\omega\),正好有\(n\)个,记为:
\(\omega_n^k=e^{2\pi ik/n}=\cos(2\pi k/n)+i\sin(2\pi k/n)\)
其中\(\omega_n=e^{2\pi i/n}=\cos(2\pi /n)+i\sin(2\pi /n)\)被称为主\(n\)次单位根,所有其他\(n\)次单位根都是\(\omega_n\)的幂次
可以把\(n\)个单位根看作是复平面上以单位圆的\(n\)个等分点为终点的向量,具体原因就是复数乘法“模长相乘,辐角相加”的规律
如图表示的是\(8\)次单位复数根在复平面上的位置
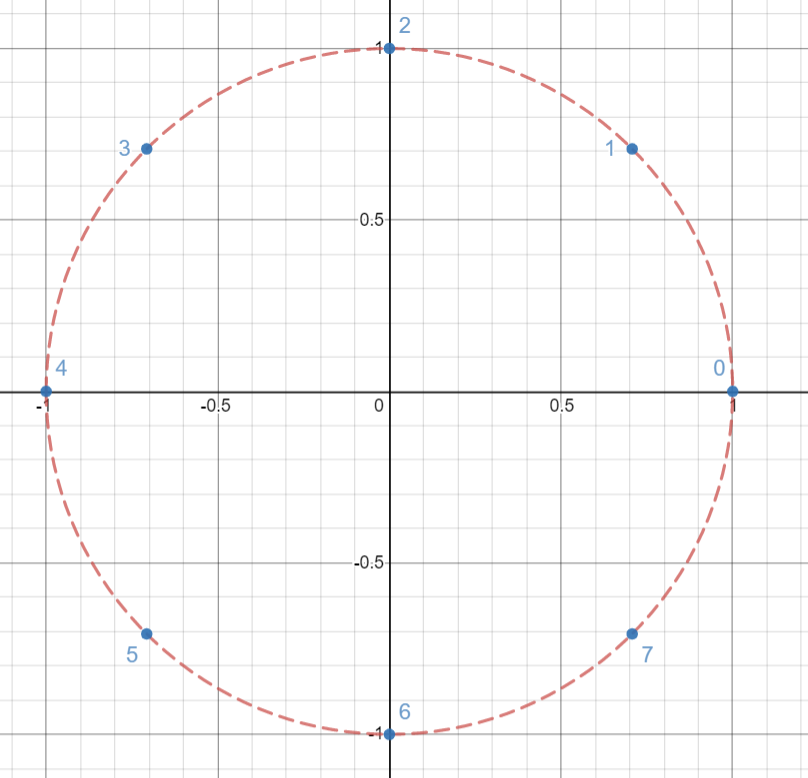
于是就可以得到规律:\(\omega_n^j\omega_n^k=\omega_n^{j+k}=\omega_n^{(j+k)\mod n}\),类似地\(\omega_n^{-1}=\omega_n^{n-1}\)
接下来的三个引理就是FFT的重头戏啦
1. 消去引理:对任何整数\(n\geqslant 0,k\geqslant 0,d>0\),有\(\omega_{dn}^{dk}=\omega_n^k\)
Proof: \(\omega_{dn}^{dk}=(e^{2\pi ihttps://img.qb5200.com/download-x/dn})^{dk}=(e^{2\pi i/n})^k=\omega_n^k\)
2. 折半引理:对任何偶数\(n\)和整数\(k\),有\((\omega_n^k)^2=(\omega_n^{k+n/2})^2=\omega_{n/2}^k\)
Proof: \((\omega_n^k)^2=\omega_n^{2k},(\omega_n^{k+n/2})^2=\omega_n^{2k+n}=\omega_n^{2k}\),最后用消去引理,\(\omega_n^{2k}=\omega_{n/2}^k\)
3. 求和引理:对任何整数\(n\geqslant 0\)与非负整数\(k:n\nmid k\),有\(\sum_{j=0}^{n-1}(\omega_n^k)^j=0\)
Proof: 利用等比数列求和公式,\(\sum_{j=0}^{n-1}(\omega_n^k)^j=\frac{1-(\omega_n^k)^n}{1-\omega_n^k}=\frac{1-\omega_n^{nk}}{1-\omega_n^k}=\frac{1-1}{1-\omega_n^k}=0\),为了使分母\(1-\omega_n^k\neq 0\),必须满足\(\omega_n^k\neq 1\implies n\nmid k\)
Part 3: 离散傅里叶变换 DFT (Discrete Fourier Transform)
DFT就是将次数界为\(n\)的多项式\(A(x)\)在\(n\)次单位复数根上求值的过程
简化一下表示方法:
\(V_n=V(\omega_n^0,\omega_n^1,\cdots,\omega_n^{n-1})=\left[\begin{matrix}1&1&1&1&\cdots&1\\1&\omega_n&\omega_n^2&\omega_n^3&\cdots&\omega_n^{n-1}\\1&\omega_n^2&\omega_n^4&\omega_n^6&\cdots&\omega_n^{2(n-1)}\\1&\omega_n^3&\omega_n^6&\omega_n^9&\cdots&\omega_n^{3(n-1)}\\\vdots&\vdots&\vdots&\vdots&\ddots&\vdots\\1&\omega_n^{n-1}&\omega_n^{2(n-1)}&\omega_n^{3(n-1)}&\cdots&\omega_n^{(n-1)(n-1)}\end{matrix} \right]\)
用公式表示就是\(V_n\pmb{a}=\pmb{y}\),也记为\(\pmb{y}=DFT_n(\pmb a)\)
另外,可以发现\([V_n]_{ij}=\omega_n^{ij}\implies y_i=\sum_{j=0}^{n-1}[V_n]_{ij}a_j=\sum_{j=0}^{n-1}\omega_n^{ij}a_j\)
终于可以看看具体操作了
Part 4: FFT
FFT利用单位根的特殊性质把DFT优化到了\(O(n\log n)\)
和分治乘法一样,按未知项次数的奇偶性分开:\(A(x)=A^{[0]}(x^2)+xA^{[1]}(x^2)\)
其中\(A^{[0]}(x)=\sum_{i=0}^{n/2-1}a_{2i}x^i,A^{[1]}(x)=\sum_{i=0}^{n/2-1}a_{2i+1}x^i\)
这时,求\(A(x)\)在\(\omega_n^0,\omega_n^1,\cdots,\omega_n^{n-1}\)的值变成了:
1. 求\(A^{[0]}(x)\)与\(A^{[1]}(x)\)在\((\omega_n^0)^2,(\omega_n^1)^2,\cdots,(\omega_n^{n-1})^2\)的值
根据折半引理,\((\omega_n^0)^2,(\omega_n^1)^2,\cdots,(\omega_n^{n-1})^2\)中两两重复,其实就是\(n/2\)个\(n/2\)次单位根
所以只要对拆开的两个多项式分别做\(DFT_{n/2}\)即可,得到\(\pmb y^{[0]}\)与\(\pmb y^{[1]}\)
2. 合并答案
\(\omega_n^{n/2}=e^{2\pi i (n/2)/n}=e^{\pi i}=-1\)(根据传说中的最美公式\(e^{i\pi}+1=0\))
所以\(\omega_n^{k+n/2}=\omega_n^k\omega_n^{n/2}=-\omega_n^k\)
所以\(y_i=y^{[0]}_i+\omega_n^i y^{[1]}_i,y_{i+n/2}=y^{[0]}_i-\omega_n^i y^{[1]}_i,i=0,1,\cdots,n/2-1\)
具体运行时,就每次循环结束时让一个初始为\(1\)的变量\(*\omega_n\)即可
递归边界:\(n=1\),那么\(w_1^0 a_0=a_0\),所以直接返回自身
计算一下时间复杂度
\(T(n)=2T(n/2)+f(n)\),其中\(f(n)=O(n)\)(合并答案)
运用主方法,\(a=2,b=2,\log_ba=\log_2 2=1\),所以\(T(n)=O(n^{\log_ba}\log n)=O(n\log n)\)(皆大欢喜)
Part 5: 离散傅里叶逆变换
可别高兴太早,还有插值哦
因为\(\pmb{y}=DFT_n(\pmb{a})=V_n\pmb{a}\),所以\(\pmb{a}=V_n^{-1}\pmb{y}\),记为\(\pmb{a}=DFT_n^{-1}(\pmb{y})\)
定理:对\(i,j=0,1,\cdots,n-1\),有\([V_n^{-1}]_{ij}=\omega_n^{-ij}/n\)
Proof: 证明\(V_n^{-1}V_n=I_n\)即可
\([V_n^{-1}V_n]_{ij}=\sum_{k=0}^{n-1}(\omega_n^{-ik}/n)\omega_n^{kj}=\frac{\sum_{k=0}^{n-1}\omega_n^{-ik}\omega_n^{kj}}{n}=\frac{\sum_{k=0}^{n-1}\omega_n^{(j-i)k}}{n}\)
如果\(i=j\),则该值\(=\frac{\sum_{k=0}^{n-1}\omega_n^0}{n}=n/n=1\)
否则,因为\(n\nmid k\),根据求和引理,该值\(=0/n=0\),所以构成了\(I_n\)
接下来\(\pmb{a}=DFT_n^{-1}(\pmb{y})=V_n^{-1}\pmb{y}\implies a_i=\sum_{j=0}^{n-1}[V_n^{-1}]_{ij}y_j=\sum_{j=0}^{n-1}(\omega_n^{-ij}/n)y_j=\frac{\sum_{j=0}^{n-1}\omega_n^{-ij}y_j}{n}\)
比较一下DFT中\(y_i=\sum_{j=0}^{n-1}\omega_n^{ij}a_j\)
只要运算时把\(\omega_n\)换成\(-\omega_n\),然后将最终答案\(/n\),就把DFT变成逆DFT了
终于可以来到激动人心的
Part 6: 递归实现
根据前文,只要将分治乘法的代码修改一下即可
可以做到直接在原址进行FFT,就是将分开的两个多项式分置在左右两边
STL提供了现成的complex类可供使用
代码中用iv表示是否为逆DFT,用o存储主单位根,用w累积
P.s 最后别忘了\(/n\),而且\(+0.5\)为了四舍五入提高精度
//This program is written by Brian Peng.
#pragma GCC optimize("Ofast","inline","no-stack-protector")
#include<bits/stdc++.h>
using namespace std;
#define Rd(a) (a=read())
#define Gc(a) (a=getchar())
#define Pc(a) putchar(a)
int read(){
register int u;register char c(getchar());register bool k;
while(!isdigit(c)&&c^'-')if(Gc(c)==EOF)exit(0);
if(c^'-')k=1,u=c&15;else k=u=0;
while(isdigit(Gc(c)))u=(u<<1)+(u<<3)+(c&15);
return k?u:-u;
}
void wr(register int a){
if(a<0)Pc('-'),a=-a;
if(a<=9)Pc(a|'0');
else wr(a/10),Pc((a%10)|'0');
}
signed const INF(0x3f3f3f3f),NINF(0xc3c3c3c3);
long long const LINF(0x3f3f3f3f3f3f3f3fLL),LNINF(0xc3c3c3c3c3c3c3c3LL);
#define Ps Pc(' ')
#define Pe Pc('\n')
#define Frn0(i,a,b) for(register int i(a);i<(b);++i)
#define Frn1(i,a,b) for(register int i(a);i<=(b);++i)
#define Frn_(i,a,b) for(register int i(a);i>=(b);--i)
#define Mst(a,b) memset(a,b,sizeof(a))
#define File(a) freopen(a".in","r",stdin),freopen(a".out","w",stdout)
double const Pi(acos(-1));
typedef complex<double> Cpx;
#define N (2100000)
Cpx o,w,a[N],b[N],tmp[N],x,y;
int n,m,s;
bool iv;
void fft(Cpx*a,int n);
signed main(){
Rd(n),Rd(m),s=1<<int(log2(n+m)+1);
Frn1(i,0,n)Rd(a[i]);
Frn1(i,0,m)Rd(b[i]);
fft(a,s),fft(b,s);
Frn0(i,0,s)a[i]*=b[i];
iv=1,fft(a,s);
Frn1(i,0,n+m)wr(a[i].real()/s+0.5),Ps;
exit(0);
}
void fft(Cpx*a,int n){
if(n==1)return;
int n2(n>>1);
Frn0(i,0,n2)tmp[i]=a[i<<1],tmp[i+n2]=a[i<<1|1];
copy(tmp,tmp+n,a),fft(a,n2),fft(a+n2,n2);
o={cos(Pi/n2),(iv?-1:1)*sin(Pi/n2)},w=1;
Frn0(i,0,n2)x=a[i],y=w*a[i+n2],a[i]=x+y,a[i+n2]=x-y,w*=o;
}Time complexity: \(O(n\log n)\)
Memory complexity: \(O(n)\)
看看效果

性能已经超过了朴素乘法(必然的),但是还是没有AC
注意到\(n,m\leqslant 1e6\),所以不仅要让时间复杂度至少\(O(n\log n)\),还要保持小的常数因子,总之递归还不够快
Part 6: 迭代实现
设\(l=\lceil\log_2(n+m+1)\rceil,s=2^l\),那么\(A(x),B(x),A(x)B(x)\)都是次数界为\(s\)的多项式
现在需要寻找到一种迭代的方式,使答案自底向上合并以减少常数因子
还是像递归版一样,把\(A^{[0]}(x)\)放在左边,\(A^{[1]}(x)\)放在右边
观察每一层递归时各个系数所在位置的规律,以\(s=8\)为例
0-> 0 1 2 3 4 5 6 7
1-> 0 2 4 6|1 3 5 7
2-> 0 4|2 6|1 5|3 7
end 0|4|2|6|1|5|3|7没看出来?那就拆成二进制看看
0-> 000 001 010 011 100 101 110 111
1-> 000 010 100 110|001 011 101 111
2-> 000 100|010 110|001 101|011 111
end 000|100|010|110|001|101|011|111显然地
一个较为感性的Proof: 因为是按照奇偶性分类,也就是说在第\(i\)层递归时判断的是该编号二进制第\(i\)位(从零开始),为\(0\)放左边,\(1\)放右边,而放右边的结果就是它的位置编号的二进制第\(l-i-1\)位是\(1\)
所以到了递归最底层,位置编号的二进制就正好是系数编号二进制前\(l\)位的反转啦
构造数组\(r_{0..s-1}\),其中\(r_i\)表示\(i\)二进制前\(l\)位的反转,可以利用递推完成,具体请自己思考(或看代码)
蝴蝶操作 (Butterfly Operation)
其实在递归版代码中已经出现,但是这里再详细说明一下
还记得\(y_i=y^{[0]}_i+\omega_n^i y^{[1]}_i,y_{i+n/2}=y^{[0]}_i-\omega_n^i y^{[1]}_i,i=0,1,\cdots,n/2-1\)吗?
但是现在不使用\(\pmb{y}\),而是\(\pmb{a}\)直接合并
因为按照奇偶性分置在两边,所以\(a^{[0]}_i=a_i,a^{[1]}_i=a_{i+n/2}\)
设\(x=a_i,y=\omega_n^i a_{i+n/2}\)
那么新的\(a_i=x+y,a_{i+n/2}=x-y\)
这就是蝴蝶操作啦
有了蝴蝶操作,只要将所有系数按照\(r\)数组的位置排列,再迭代合并,就完成了FFT
在代码中,用\(i,i_2\)表示当前合并产生的和开始的序列长度,\(j\)表示合并序列的开头位置,\(k\)控制每一位的合并,上代码
//This program is written by Brian Peng.
#pragma GCC optimize("Ofast","inline","no-stack-protector")
#include<bits/stdc++.h>
using namespace std;
#define Rd(a) (a=read())
#define Gc(a) (a=getchar())
#define Pc(a) putchar(a)
int read(){
register int u;register char c(getchar());register bool k;
while(!isdigit(c)&&c^'-')if(Gc(c)==EOF)exit(0);
if(c^'-')k=1,u=c&15;else k=u=0;
while(isdigit(Gc(c)))u=(u<<1)+(u<<3)+(c&15);
return k?u:-u;
}
void wr(register int a){
if(a<0)Pc('-'),a=-a;
if(a<=9)Pc(a|'0');
else wr(a/10),Pc((a%10)|'0');
}
signed const INF(0x3f3f3f3f),NINF(0xc3c3c3c3);
long long const LINF(0x3f3f3f3f3f3f3f3fLL),LNINF(0xc3c3c3c3c3c3c3c3LL);
#define Ps Pc(' ')
#define Pe Pc('\n')
#define Frn0(i,a,b) for(register int i(a);i<(b);++i)
#define Frn1(i,a,b) for(register int i(a);i<=(b);++i)
#define Frn_(i,a,b) for(register int i(a);i>=(b);--i)
#define Mst(a,b) memset(a,b,sizeof(a))
#define File(a) freopen(a".in","r",stdin),freopen(a".out","w",stdout)
double const Pi(acos(-1));
typedef complex<double> Cpx;
#define N (2100000)
Cpx a[N],b[N],o,w,x,y;
int n,m,l,s,r[N];
void fft(Cpx*a,bool iv);
signed main(){
Rd(n),Rd(m),s=1<<(l=log2(n+m)+1);
Frn1(i,0,n)Rd(a[i]);
Frn1(i,0,m)Rd(b[i]);
Frn0(i,0,s)r[i]=(r[i>>1]>>1)|((i&1)<<(l-1));
fft(a,0),fft(b,0);
Frn0(i,0,s)a[i]*=b[i];
fft(a,1);
Frn1(i,0,n+m)wr(a[i].real()+0.5),Ps;
exit(0);
}
void fft(Cpx*a,bool iv){
Frn0(i,0,s)if(i<r[i])swap(a[i],a[r[i]]);
for(int i(2),i2(1);i<=s;i2=i,i<<=1){
o={cos(Pi/i2),(iv?-1:1)*sin(Pi/i2)};
for(int j(0);j<s;j+=i){
w=1;
Frn0(k,0,i2){
x=a[j+k],y=w*a[j+k+i2];
a[j+k]=x+y,a[j+k+i2]=x-y,w*=o;
}
}
}
if(iv)Frn0(i,0,s)a[i]/=s;
}Time complexity: \(O(n\log n)\)
Memory complexity: \(O(n)\)
看看效果

终于……
到现在为止FFT的内容已经全部结束啦,下面是拓展部分
Extension: 快速数论变换 NTT (Number Theoretic Transform)
虽然FFT具有优秀的时间复杂度,但因为用到了复数,不可避免会出现精度问题
如果多项式系数和结果都是一定范围非负整数,可以考虑使用NTT来优化精度和时空常数
Reference:
《算法导论》
自为风月马前卒:快速数论变换(NTT)小结
Prerequisite knowledge:
FFT(必须知道的)
模运算基本知识
原根的性质
现在考虑所有运算都在\(mod P\)意义下
设有正整数\(g\),如果在\(g\)的次幂能够得到\(<P\)的任何正整数,那么称\(g\)是\(Z_P^*\)的原根,其中\(Z_P^*\)是模\(P\)乘法群,在这里不多作解释
E.g 对于\(P=7\),计算所有\(<P\)的正整数的次幂构成的集合
1-> {1}
2-> {1,2,4}
3-> {1,2,3,4,5,6}
4-> {1,2,4}
5-> {1,2,3,4,5,6}
6-> {1,6}所以\(3,5\)就是\(Z_7^*\)的原根
在代码中,一般使用大质数\(P=998244353,g=3\)
原根的特点就是它的次幂以长度为\(\phi(P)\)循环
E.g \(P=7,g=3\)
那么\(g\)的次幂(从\(g^0\))开始分别是:\(1,3,2,6,4,5,1,3,2,6,4,5,\cdots\)
这个特性和单位根非常相似
但是要完全替换单位根,还差一步
单位根的代替品
在FFT中使用的是循环长度为\(n\),且满足消去引理和求和引理的\(n\)次单位复数根(折半引理由消去引理推出,故不考虑)
所以为了让循环长度为\(n\),我们不直接使用原根,而是原根的次幂
离散对数定理:如果\(g\)是\(Z_P^*\)的一个原根,则\(x\equiv y(\mod\phi(P))\iff g^x\equiv g^y(\mod P)\)
Proof: 设\(x\equiv y(\mod\phi(P))\),则对某个整数\(k\)有\(x=y+k\phi(P)\)
因此\(g^x\equiv g^{y+k\phi(P)} \equiv g^y (g^{\phi(P)})^k \equiv g^y 1^k \equiv g^y (\mod P)\)(根据欧拉定理)
反过来,因为循环长度是\(\phi(P)\),必定有\(x\equiv y(\mod\phi(P))\)
现在考虑有一个\(g\)的次幂\(g^q\)满足\(g^q\)的次幂以长度\(n\)循环
也就是说对任意整数\(x\geqslant0,0<y<n\),有\(g^{qx}\equiv g^{q(x+n)}\not\equiv g^{q(x+y)}(\mod P)\)
即\(qx\equiv q(x+n)\not\equiv q(x+y)(\mod \phi(P))\)
即\(0\equiv qn\not\equiv qy(\mod \phi(P))\)
可得\(\phi(P)|qn,\phi(P)\nmid qy\)
那么为了使\(q\)的因数数量最小化,\(q=\phi(P)/n\)
此时\(qy-\phi(P)y/n\)
因为\(y<n\),所以\(qy<\phi(P)\),必定有\(\phi(P)\nmid qy\)
所以\(q=\phi(P)/n\)是可取的
那么问题来了,万一\(\phi(P)/n\)不是整数怎么办?
这就引出了大质数\(P=998244353\)的另一个性质:\(\phi(P)=P-1=998244352=2^{23}\cdot 7\cdot 17\)
而根据数据范围\(n,m\leqslant1e6\),可知\(l\leqslant 21\),所以\(q\)总是整数(真是一个神奇的数字)
总结一下,\(g^{\phi(P)/n}=g^{\frac{P-1}{n}}\)就是\(\omega_n\)的代替者
消去引理(只需考虑\(d=2\)的情况)和求和引理就请大家自己证明了(其实道理都非常相似)
最后只要把\(\omega_n\)替换掉,运算都改为模\(P\)意义下的运算即可,在算\(-\omega_n\)时要用到\(g^{-1}=332748118\),还有最后答案别忘了\(*s^{-1}\),上代码
//This program is written by Brian Peng.
#pragma GCC optimize("Ofast","inline","no-stack-protector")
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define Rd(a) (a=read())
#define Gc(a) (a=getchar())
#define Pc(a) putchar(a)
int read(){
register int u;register char c(getchar());register bool k;
while(!isdigit(c)&&c^'-')if(Gc(c)==EOF)exit(0);
if(c^'-')k=1,u=c&15;else k=u=0;
while(isdigit(Gc(c)))u=(u<<1)+(u<<3)+(c&15);
return k?u:-u;
}
void wr(register int a){
if(a<0)Pc('-'),a=-a;
if(a<=9)Pc(a|'0');
else wr(a/10),Pc((a%10)|'0');
}
signed const INF(0x3f3f3f3f),NINF(0xc3c3c3c3);
long long const LINF(0x3f3f3f3f3f3f3f3fLL),LNINF(0xc3c3c3c3c3c3c3c3LL);
#define Ps Pc(' ')
#define Pe Pc('\n')
#define Frn0(i,a,b) for(register int i(a);i<(b);++i)
#define Frn1(i,a,b) for(register int i(a);i<=(b);++i)
#define Frn_(i,a,b) for(register int i(a);i>=(b);--i)
#define Mst(a,b) memset(a,b,sizeof(a))
#define File(a) freopen(a".in","r",stdin),freopen(a".out","w",stdout)
#define P (998244353)
#define G (3)
#define Gi (332748118)
#define N (2100000)
int n,m,l,s,r[N],a[N],b[N],o,w,x,y,siv;
int fpw(int a,int p){return p?a>>1?(p&1?a:1)*fpw(a*a%P,p>>1)%P:a:1;}
void ntt(int*a,bool iv);
signed main(){
Rd(n),Rd(m),siv=fpw(s=1<<(l=log2(n+m)+1),P-2);
Frn1(i,0,n)Rd(a[i]);
Frn1(i,0,m)Rd(b[i]);
Frn0(i,0,s)r[i]=(r[i>>1]>>1)|((i&1)<<(l-1));
ntt(a,0),ntt(b,0);
Frn0(i,0,s)a[i]=a[i]*b[i]%P;
ntt(a,1);
Frn1(i,0,n+m)wr(a[i]),Ps;
exit(0);
}
void ntt(int*a,bool iv){
Frn0(i,0,s)if(i<r[i])swap(a[i],a[r[i]]);
for(int i(2),i2(1);i<=s;i2=i,i<<=1){
o=fpw(iv?Gi:G,(P-1)/i);
for(int j(0);j<s;j+=i){
w=1;
Frn0(k,0,i2){
x=a[j+k],y=w*a[j+k+i2]%P;
a[j+k]=(x+y)%P,a[j+k+i2]=(x-y+P)%P,w=w*o%P;
}
}
}
if(iv)Frn0(i,0,s)a[i]=a[i]*siv%P;
}Time complexity: \(O(n\log n)\)
Memory complexity: \(O(n)\)
看看效果

时间上的提升效果不大,但是空间少了一半(因为用了int而不是complex)
Conclusion:
打了一天的博客终于写完了(好累)
但是对FFT和NTT的理解也加深了不少
这个算法对数学知识和分治思想的要求都很高
本蒟蒻花了近一年的时间才真正理解
如果有错误和意见请大佬多多指教
那么本篇博客就到这里啦,谢谢各位大佬的支持!ありがとう!
加载全部内容