Deep Clustering Algorithms

作者：凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/

    本文研究路线：深度自编码器(Deep Autoencoder)->Deep Embedded Clustering(DEC)->Improved Deep Embedded clustering(IDEC)->Deep Fuzzy K-means(DFKM)，其中Deep Autoencoder已经在深度自编码器(Deep Autoencoder)MATLAB解读中提到，也有很多深度自编码器的改进方法，不详细讲解，重点谈深度聚类算法。如有不对之处，望指正。

    深度聚类算法的网络架构图

    深度聚类算法的损失函数

1. Deep Embedded Clustering

1.1 Stochastic Neighbor Embedding (SNE)

    SNE是一种非线性降维策略，两个特征之间存在非线性相关性，主要用于数据可视化，PCA（主成成分分析）是一种线性降维策略，两个特征之间存在线性相关性。SNE在原始空间(高维空间)中利用Gauss分布将数据点之间的距离度量转化为条件概率，在映射空间(低维空间)中利用Gauss分布将映射点之间的距离度量转化为条件概率，并利用KL散度来最小化高维空间与低维空间的条件概率。

    SNE面临的问题有两个：（1）KL散度是一种非对称度量，（2）拥挤问题。对于非对称问题，定义pij，将非对称度量转化为对称度量。但对称度量仍然面临拥挤问题，映射到低维空间中，映射点之间不能根据数据本身的特性很好地分开。

    对于拥挤问题(The Crowding Problem)的解决，提出t-SNE，一种非线性降维策略，主要用于可视化数据。引入厚尾部的学生t分布，将低维空间映射点之间的距离度量转化为概率分布t分布qij，使得不同簇之间的点能很好地分开。

1.2 t-SNE

1.3 Deep Embedded Clustering(DEC)

    受t-SNE的启发，提出DEC算法，重新定义原始空间(高维空间)的度量pij。微调阶段，舍弃掉编码器层，最小化KL散度作为损失函数，迭代更新参数。

2. Improved Deep Embedded Clustering(IDEC)

    DEC丢弃解码器层，并使用聚类损失Lc对编码器进行微调。作者认为这种微调会扭曲嵌入空间，削弱嵌入特征的代表性，从而影响聚类性能。因此，提出保持解码器层不变，直接将聚类损失附加到嵌入空间。

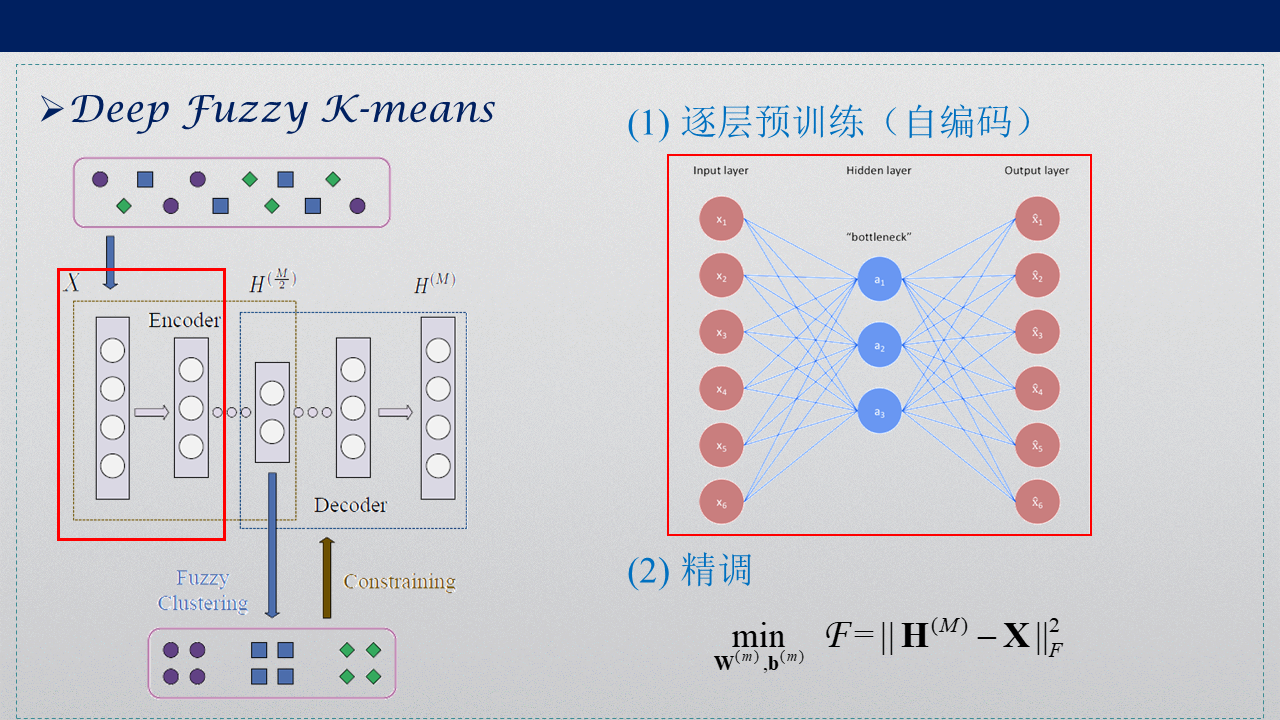
3. Deep Fuzzy K-means

    Deep Fuzzy K-means同样在低维映射空间中加入聚类过程，将特征提取与聚类同时进行，引入熵加权的模糊K-means，不采用原来的欧氏距离，而是自己重新定义度量准则，权值偏置的正则化项防止过拟合，提高泛化能力。

4. 参考文献

[1] Maaten L, Hinton G. Visualizing data using t-SNE[J]. Journal of machine learning research, 2008, 9(Nov): 2579-2605.

[2] Vincent P, Larochelle H, Lajoie I, et al. Stacked denoising autoencoders: Learning useful representations in a deep network with a local denoising criterion[J]. Journal of machine learning research, 2010, 11(Dec): 3371-3408.

[3] Xie J, Girshick R, Farhadi A. Unsupervised deep embedding for clustering analysis[C]//International conference on machine learning. 2016: 478-487.

[4] Guo X, Gao L, Liu X, et al. Improved deep embedded clustering with local structure preservation[C]//IJCAI. 2017: 1753-1759.

[5] Zhang R, Li X, Zhang H, et al. Deep Fuzzy K-Means with Adaptive Loss and Entropy Regularization[J]. IEEE Transactions on Fuzzy Systems, 2019.

[6] t-SNE相关资料：t-SNE完整笔记、An illustrated introduction to the t-SNE algorithm、从SNE到t-SNE再到LargeVis、t-SNE算法-CSDN

[7] DEC与IDEC的Python代码-Github

[8] DFKM的Python代码-Github