Project Euler 60: Prime pair sets
sorrowise 人气:3素数3, 7, 109, 673很有意思,从中任取两个素数以任意顺序拼接起来形成的仍然是素数。例如,取出7和109,7109和1097都是素数。这四个素数的和是792,是具有这样性质的四个素数的最小的和。求满足以上性质的五个素数的最小的和。
分析:这道题的解法非常让人出人意料,这个问题实际上和图论中的的分团问题有关。要理解这个问题,我们需要知道一点图论中的基础知识。如果你已经对图论比较了解了,这一段可以跳过。图论属于组合数学的一个分支,图是图论的主要研究对象。所谓图是指由若干给定的顶点及连接两顶点的边所构成的图形,这种图形通常用来描述某些事物之间的关系。顶点用于代表事物,连接两顶点的边则用于表示两个事物间具有这种关系。图按其中的边是否有方向性可以分为有向图和无向图,按边是否有权重可以分为有权重图和无权重图,我们今天这里讨论的只是无权重的无向图,其它类型的图这里就不涉及了。
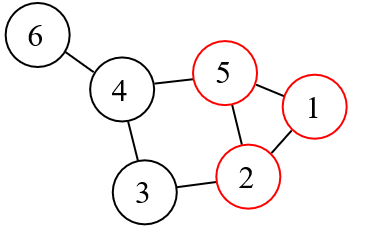
回到这里的问题,题目要求我们求出满足性质的五个素数的最小和,则我们首先需求找到这些满足性质的素数。这个性质即这些素数中两两之间可以正向和反向拼接仍能构成素数。我们可以把这些素数想像成为图中的节点,如果两个素数之间满足题目所说的性质,则我们可以在这两个素数之间画一条边。那么题目的问题就可以转换成,在一个由素数构成的图找到满足条件的五个顶点,这五个顶点两两之间都是联通的。现在我们可以明显看出来,这实际上就是图论中的分团问题。所谓分团问题(clique problem)是在一个图中找到一个完全子图,这个完全子图中的顶点两两之间都是相连接的。分团问题的一个典型应用是在社交网络分析当中,我们可以用图的顶点代表个人,用图的边代表两人之间相互认识,那么分团问题就相当于在某个人群找到一个小团体,这个小团体各个成员相互之间都认识。如在下图由六个顶点构成的图中,{1, 2, 5}三个顶点就构成了一个团,因为它们两两之间都相互连接的。
绝大部分分团问题都是困难的,即不存在多项式时间算法,但也存在一些比暴力求解更优的算法,如著名的Bron–Kerbosch算法,算法的细节大家可以参见这里。考虑到python中已经有比较完善的图论和网络分析的库也就是networkx,所以我们直接调用这个库来解决题目中的问题,这个库的使用方法请参见文档。首先我们要生成符合条件的素数对,我们编写了一个函数来判断特定的两个函数是否符合题目中的性质,这里一个优化的小细节是,大于三的所有素数期各位数之和除三的余数要不为一要不为二,当把两个素数拼接起来其各位数之和正好为两个素数的各位数之和的和,因此要满足题目的性质,这两个素数的各位数之和除三的余数必须要相同,否则两者拼接起来后各位数之和必然除三余零,即会被三整除不可能是一个素数。考虑到大于三的数和其各位数之和模三同余,则我们只需要比较两个素数除以三的余数是否相同就可以了。因为在判断两个素数是否满足性质时,同余运算比数字转字符串再拼接再转整数再判断是否为素数要快的多,因此在判断时先判断是否满足同余性质,不满足则不需要再进行之后的操作,从而可以大大节省判断的时间。
需要注意的是,在我们求满足条件的素数对时,需要给定一个合理的上界,这里只能先猜测,我首先把上界定到一万,求出小于一万的所有满足条件的素数对。然后把些素数对输入到networkx的图对象,成为这个图的一条条边,然后在这个图中使用find_cliques函数找到所有顶点数为五的子图(这个函数实际上使用的是改进过的Bron–Kerbosch算法),然后在这些满足条件的子图中求出各个顶点之和的最小值。事实上,在一万的上界以内,满足条件的素数集合实际上只有一个,也就是 {13, 8389, 5701, 5197, 6733}这五个素数。为了验证以上素数集合确实是和最小的,我又求了十万以下的所有满足条件的素数集合,上面的给出的这个素数集合确实是和最小的,因此符合题目的所有条件。
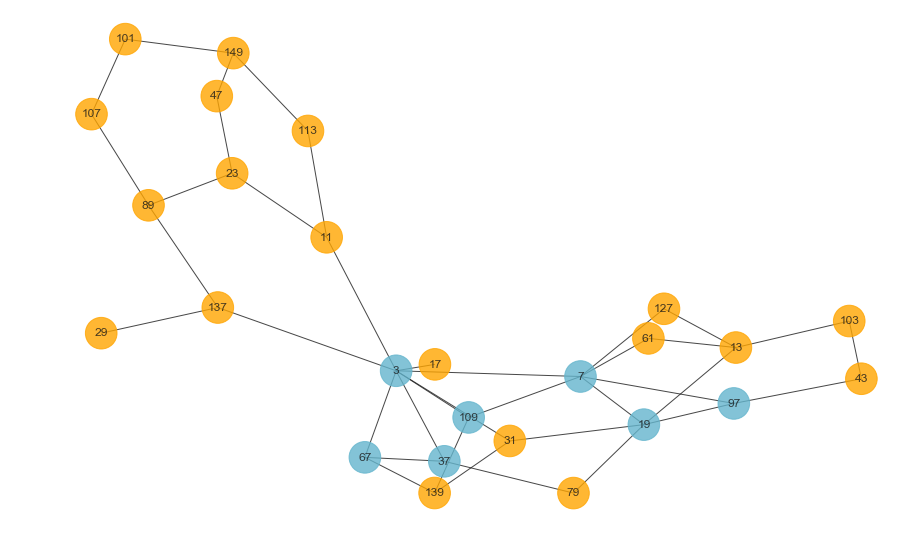
最后一点可视化的工作:下图展示了一百五以内的所有素数中,满足题目中性质且大小为三的素数集合,可以明显发现共有三对(已经用青色标出),分别是{3, 7, 109}, {3, 37, 67}和{7, 19, 97}。可以看到,用图论解决题目中的问题是相当优雅且直观的。
最后,解题的代码如下:
# time cost = 2.82 s ± 83.9 ms
from sympy import isprime,primerange
import networkx as nx
from networkx.algorithms.clique import find_cliques
def is_pair_prime(x,y):
conc = lambda x,y:isprime(int(str(x)+str(y)))
if x == 3:
return conc(x,y) and conc(y,x)
else:
r = x % 3
return y%3==r and conc(x,y) and conc(y,x)
def main(N=8400):
res = []
primes = list(primerange(3,N))
index = 0
for p in primes:
index += 1
for i in primes[index:]:
if is_pair_prime(p,i):
res.append((p,i))
G = nx.Graph()
G.add_edges_from(res)
ans = [clique for clique in find_cliques(G) if len(clique)==5]
return min(map(sum,ans))加载全部内容