Project Euler 58: Spiral primes
sorrowise 人气:1从一开始按以下方式逆时针旋转,可以形成一个边长为七的正方形螺旋:
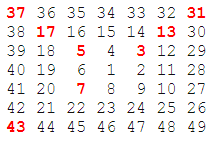
一个有趣的现象是右下对角线上都有一个奇完全平方数,但是更有趣的是两条对角线上的十三个数中有八个数是素数(已经标红),也就是说素数占比为\(8/13\approx62\%\)。如果在上面的螺旋再加一层就可以形成一个边长为九的正文形螺旋。如果这个过程继续下去,在边长为多少的时候两条对角线上的数字中质数占比会低于10%?
分析:这道题和第二十八题非常类似,只不过二十八题是顺时针旋转,所以是右上角元素是完全平方数,而这道题是逆时针旋转,所以右下角元素是完全平方数。回忆二十八题的解题思路,我们从每一层的完全平方数开始,依次递推同一层的另外三个对角线元素的值。这道题也是一样的思路,首先观察每一层右下角的奇完全平方数,如边长为七时右下角的奇完全平方数是四十九,然后从四十九中减去六就得到左下角的对角线元素是四十三,而六恰好是边长七减去一。依次类推,我们从四十三中减去六得到左上角的对角线元素为三十七,再减去六得到右上角对角线元素为三十一。在这四个数中,右下角的完全平方数显然不是素数,所以我们只需要检测剩下三个元素是否是素数就可以了。
一般地,设每一层螺旋的边长为\(k\),显然\(k\)只能取大于一的奇数值。则这一层的右下角元素值为\(k^2\),左下角元素为\(k^2-(k-1)\),左上角元素为\(k^2-2(k-1)\),右上角元素为\(k^2-3(k-1)\)。在每一层,我们检查除右下角元素以外的其它三个元素是否为素数,假设到目前这一层为止总共在对角线上发现了\(p\)个素数,而对角线上元素共有\(2k-1\)个,则素数占比\(r=p/(2k-1)\),当\(r<0.1\)时返回\(k\)即为题目所求。代码如下:
# time cost = 276 ms ± 1.39 ms
from itertools import count
from sympy import isprime
def main():
k = 0
for i in count(3,2):
a = i**2 - (i-1)
b = a - (i-1)
c = b - (i-1)
k += len([x for x in [a,b,c] if isprime(x)])
n = 2 * i - 1
if k/n < 0.1:
return i加载全部内容