JavaScript中数据结构与算法(三):链表
人气:3我们可以看到在javascript概念中的队列与栈都是一种特殊的线性表的结构,也是一种比较简单的基于数组的顺序存储结构。由于javascript的解释器针对数组都做了直接的优化,不会存在在很多编程语言中数组固定长度的问题(当数组填满后再添加就比较困难了,包括添加删除,都是需要把数组中所有的元素全部都变换位置的,javascript的的数组确实直接给优化好了,如push,pop,shift,unshift,split方法等等…)
线性表的顺序存储结构,最大的缺点就是改变其中一个元素的排列时都会引起整个合集的变化,其原因就是在内存中的存储本来就是连贯没有间隙的,删除一个自然就要补上。针对这种结构的优化之后就出现了链式存储结构,换个思路,我们完全不关心数据的排列,我们只需要在每一个元素的内部把下一个的数据的位置给记录就可以了,所以用链接方式存储的线性表简称为链表,在链式结构中,数据=(信息+地址)
链式结构中,我们把地址也可以称为“链”,一个数据单元就是一个节点,那么可以说链表就是一组节点组成的合集。每一个节点都有一个数据块引用指向它的下一个节点
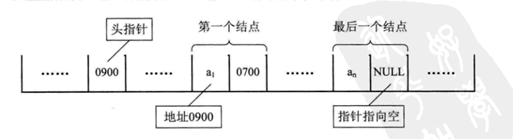
数组元素是靠位置关系做逻辑引用,链表则是靠每一个数据元保存引用指针关系进行引用
这种结构上的优势就非常明显的,插入一个数据完全不需要关心其排列情况,只要把“链”的指向衔接上
这样做链表的思路就不会局限在数组上了,我们可以用对象了,只要对象之间存在引用关系即可
链表一般有,单链表、静态链表、循环链表、双向链表
单链表:就是很单一的向下传递,每一个节点只记录下一个节点的信息,就跟无间道中的梁朝伟一样做卧底都是通过中间人上线与下线联系,一旦中间人断了,那么就无法证明自己的身份了,所以片尾有一句话:"我是好人,谁知道呢?”
静态链表:就是用数组描述的链表。也就是数组中每一个下表都是一个“节”包含了数据与指向
循环链表:由于单链表的只会往后方传递,所以到达尾部的时候,要回溯到首部会非常麻烦,所以把尾部节的链与头连接起来形成循环
双向链表:针对单链表的优化,让每一个节都能知道前后是谁,所以除了后指针域还会存在一个前指针域,这样提高了查找的效率,不过带来了一些在设计上的复杂度,总体来说就是空间换时间了
综合下,其实链表就是线性表中针对顺序存储结构的一种优化手段,但是在javascript语言中由于数组的特殊性(自动更新引用位置),所以我们可以采用对象的方式做链表存储的结构
单链表
我们实现一个最简单的链表关系
function createLinkList() {
var _this = {},
prev = null;
return {
add: function(val) {
//保存当前的引用
prev = {
data: val,
next: prev || null
}
}
}
}
var linksList = createLinkList();
linksList.add("arron1");
linksList.add("arron2");
linksList.add("arron3");
//node节的next链就是 -arron3-arron2-arron1
通过node对象的next去直引用下一个node对象,初步是实现了通过链表的引用,这种链式思路jQuery的异步deferred中的then方法,还有日本的cho45的jsderferre中都有用到。这个实现上还有一个最关键的问题,我们怎么动态插入数据到执行的节之后?
所以我们必须 要设计一个遍历的方法,用来搜索这个node链上的数据,然后找出这个对应的数据把新的节插入到当前的链中,并改写位置记录
//在链表中找到对应的节
var findNode = function createFindNode(currNode) {
return function(key){
//循环找到执行的节,如果没有返回本身
while (currNode.data != key) {
currNode = currNode.next;
}
return currNode;
}
}(headNode);
这就是一个查找当前节的一个方法,通过传递原始的头部headNode节去一直往下查找next,直到找到对应的节信息
这里是用curry方法实现的
那么插入节的的时候,针对链表地址的换算关系这是这样
a-b-c-d的链表中,如果要在c(c.next->d)后面插入一个f
a-b-c-f-d ,那么c,next->f , f.next-d
通过insert方法增加节
//创建节
function createNode(data) {
this.data = data;
this.next = null;
}
//初始化头部节
//从headNode开始形成一条链条
//通过next衔接
var headNode = new createNode("head");
//在链表中找到对应的节
var findNode = function createFindNode(currNode) {
return function(key){
//循环找到执行的节,如果没有返回本身
while (currNode.data != key) {
currNode = currNode.next;
}
return currNode;
}
}(headNode);
//插入一个新节
this.insert = function(data, key) {
//创建一个新节
var newNode = new createNode(data);
//在链条中找到对应的数据节
//然后把新加入的挂进去
var current = findNode(key);
//插入新的接,更改引用关系
//1:a-b-c-d
//2:a-b-n-c-d
newNode.next = current.next;
current.next = newNode;
};
首先分离出createNode节的构建,在初始化的时候先创建一个头部节对象用来做节开头的初始化对象
在insert增加节方法中,通过对headNode链的一个查找,找到对应的节,把新的节给加后之后,最后就是修改一下链的关系
如何从链表中删除一个节点?
由于链表的特殊性,我们a->b->c->d ,如果要删除c那么就必须修改b.next->c为 b.next->d,所以找到前一个节修改其链表next地址,这个有点像dom操作中removeChild找到其父节点调用移除子节点
同样的我们也在remove方法的设计中,需要设计一个遍历往上回溯一个父节点即可
//找到前一个节
var findPrevious = function(currNode) {
return function(key){
while (!(currNode.next == null) &&
(currNode.next.data != key)) {
currNode = currNode.next;
}
return currNode;
}
}(headNode);
//插入方法
this.remove = function(key) {
var prevNode = findPrevious(key);
if (!(prevNode.next == null)) {
//修改链表关系
prevNode.next = prevNode.next.next;
}
};
测试代码:
<!doctype html><button id="test1">插入多条数据</button>
<button id="test2">删除Russellville数据</button><div id="listshow"><br /></div><script type="text/javascript">
//////////
//创建链表 //
//////////
function createLinkList() {
//创建节
function createNode(data) {
this.data = data;
this.next = null;
}
//初始化头部节
//从headNode开始形成一条链条
//通过next衔接
var headNode = new createNode("head");
//在链表中找到对应的节
var findNode = function createFindNode(currNode) {
return function(key) {
//循环找到执行的节,如果没有返回本身
while (currNode.data != key) {
currNode = currNode.next;
}
return currNode;
}
}(headNode);
//找到前一个节
var findPrevious = function(currNode) {
return function(key) {
while (!(currNode.next == null) &&
(currNode.next.data != key)) {
currNode = currNode.next;
}
return currNode;
}
}(headNode);
//插入一个新节
this.insert = function(data, key) {
//创建一个新节
var newNode = new createNode(data);
//在链条中找到对应的数据节
//然后把新加入的挂进去
var current = findNode(key);
//插入新的接,更改引用关系
//1:a-b-c-d
//2:a-b-n-c-d
newNode.next = current.next;
current.next = newNode;
};
//插入方法
this.remove = function(key) {
var prevNode = findPrevious(key);
if (!(prevNode.next == null)) {
//修改链表关系
prevNode.next = prevNode.next.next;
}
};
this.display = function(fn) {
var currNode = headNode;
while (!(currNode.next == null)) {
currNode = currNode.next;
fn(currNode.data)
}
};
}
var cities = new createLinkList();
function create() {
var text = '';
cities.display(function(data) {
text += '-' + data;
});
var div = document.createElement('div')
div.innerHTML = text;
document.getElementById("listshow").appendChild(div)
}
document.getElementById("test1").onclick = function() {
cities.insert("Conway", "head");
cities.insert("Russellville", "Conway");
cities.insert("Carlisle", "Russellville");
cities.insert("Alma", "Carlisle");
create();
}
document.getElementById("test2").onclick = function() {
cities.remove("Russellville");
create()
}
</script>
双链表
原理跟单链表是一样的,无非就是给每一个节增加一个前链表的指针

增加节
//插入一个新节
this.insert = function(data, key) {
//创建一个新节
var newNode = new createNode(data);
//在链条中找到对应的数据节
//然后把新加入的挂进去
var current = findNode(headNode,key);
//插入新的接,更改引用关系
newNode.next = current.next;
newNode.previous = current
current.next = newNode;
};
删除节
this.remove = function(key) {
var currNode = findNode(headNode,key);
if (!(currNode.next == null)) {
currNode.previous.next = currNode.next;
currNode.next.previous = currNode.previous;
currNode.next = null;
currNode.previous = null;
}
};
在删除操作中有一个明显的优化:不需要找到父节了,因为双链表的双向引用所以效率比单链要高
测试代码:
<!doctype html><button id="test1">插入多条数据</button>
<button id="test2">删除Russellville数据</button><div id="listshow"><br /></div><script type="text/javascript">
//////////
//创建链表 //
//////////
function createLinkList() {
//创建节
function createNode(data) {
this.data = data;
this.next = null;
this.previous = null
}
//初始化头部节
//从headNode开始形成一条链条
//通过next衔接
var headNode = new createNode("head");
//在链表中找到对应的数据
var findNode = function(currNode, key) {
//循环找到执行的节,如果没有返回本身
while (currNode.data != key) {
currNode = currNode.next;
}
return currNode;
}
//插入一个新节
this.insert = function(data, key) {
//创建一个新节
var newNode = new createNode(data);
//在链条中找到对应的数据节
//然后把新加入的挂进去
var current = findNode(headNode,key);
//插入新的接,更改引用关系
newNode.next = current.next;
newNode.previous = current
current.next = newNode;
};
this.remove = function(key) {
var currNode = findNode(headNode,key);
if (!(currNode.next == null)) {
currNode.previous.next = currNode.next;
currNode.next.previous = currNode.previous;
currNode.next = null;
currNode.previous = null;
}
};
this.display = function(fn) {
var currNode = headNode;
while (!(currNode.next == null)) {
currNode = currNode.next;
fn(currNode.data)
}
};
}
var cities = new createLinkList();
function create() {
var text = '';
cities.display(function(data) {
text += '-' + data;
});
var div = document.createElement('div')
div.innerHTML = text;
document.getElementById("listshow").appendChild(div)
}
document.getElementById("test1").onclick = function() {
cities.insert("Conway", "head");
cities.insert("Russellville", "Conway");
cities.insert("Carlisle", "Russellville");
cities.insert("Alma", "Carlisle");
create();
}
document.getElementById("test2").onclick = function() {
cities.remove("Russellville");
create()
}
</script>
git代码下载:https://github.com/JsAaronhttps://img.qb5200.com/download-x/data_structure.git
加载全部内容