python肯德尔系数相关性数据分析示例
fanstuck 人气:0前言
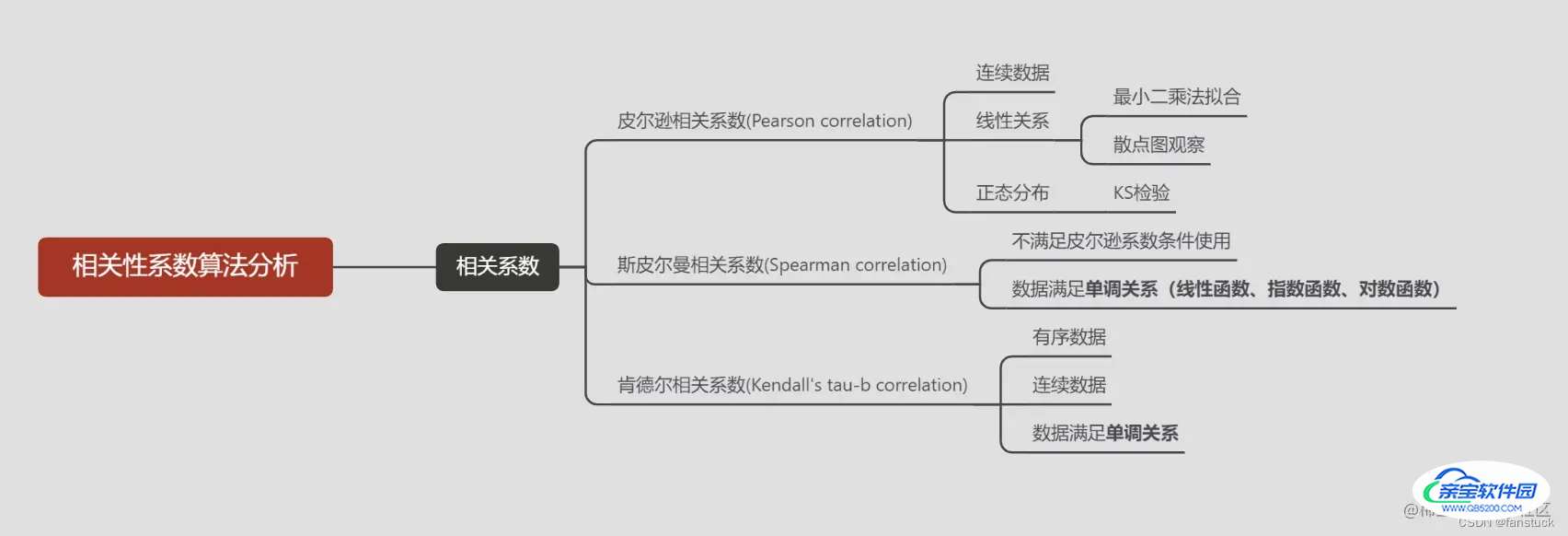
相关性分析算是很多算法以及建模的基础知识之一了,十分经典。关于许多特征关联关系以及相关趋势都可以利用相关性分析计算表达。其中常见的相关性系数就有三种:person相关系数,spearman相关系数,Kendall's tau-b等级相关系数。各有各自的用法和使用场景。当然关于这以上三种相关系数的计算算法和原理+代码我都会在我专栏里面写齐全。目前关于数学建模的专栏已经将传统的机器学习预测算法、维度算法、时序预测算法和权重算法写的七七八八了,有这个需求兴趣的同学可以去看看。
一、定义
Kendall(肯德尔)系数的定义:n个同类的统计对象按特定属性排序,其他属性通常是乱序的。同序对(concordant pairs)和异序对(discordant pairs)之差与总对数(n*(n-1)/2)的比值定义为Kendall(肯德尔)系数。
与斯皮尔曼秩相关相似的是,肯德尔相关也是一种秩相关系数,是基于数据对象的秩(rank)来进行两个(随机变量)之间的相关关系(强弱和方向)的评估。所分析的目标对象应该是一种有序的类别变量,比如名次、年龄段、肥胖等级(重度肥胖,中度肥胖、轻度肥胖、不肥胖)等。
不同的是,斯皮尔曼相关是基于秩差(比如说,小明在班级中的历史成绩排名为10,英语成绩排名为4,那么在这个班级的学生的历史成绩和英语成绩的斯皮尔曼相关分析中,小明的成绩的贡献就是(10-4=6) )来进行相关关系的评估;而肯德尔相关则是基于样本数据对之间的关系来进行相关系数的强弱的分析,数据对可以分为一致对(Concordant)和分歧对(Discordant)。
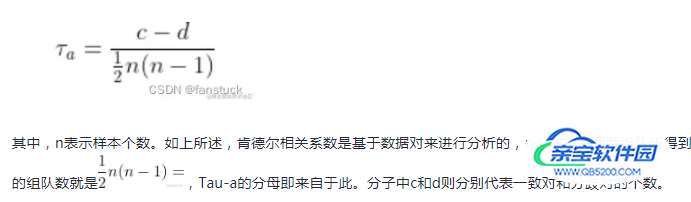
kendall相关系数的计算公式如下:

假如我们设一组8人的身高和体重在那里A的人是最高的,第三重,等等:

注意,A最高,但体重排名为 3 ,比体重排名为 4,5,6,7,8 的重,贡献5个同序对,即AB,AE,AF,AG,AH。同理,我们发现B、C、D、E、F、G、H分别贡献4、5、4、3、1、0、0个同序对,因此,同序对数
P = 5 + 4 + 5 + 4 + 3 + 1 + 0 + 0 = 22.
异序对数 Q=28-22 (总对数减去同序对数为异序对数)
因而R=((22-6)/28)=0.57。这一结果显示出强大的排名之间的规律,符合预期。 我们看到,有一些相关的两个排名之间的相关性,可以使用肯德尔头系数,客观地衡量对应。
- 如果两个排名之间的一致性是完美的(即两个排名相同),则系数的值为1。
- 如果两个排名之间的分歧是完美的(即,一个排名与另一个排名相反),则系数具有值-1。
- 如果X和Y是独立的,那么我们期望系数近似为零。
二、使用条件
在适用肯德尔相关分析前首先要检查数据是否满足以下基本假设,满足了这些基本假设才能确保你所得到的相关分析结果是有效的。
- 变量数据是有序的( ordinal) 或者是连续的(continuous). 有序尺度(Ordinal scales )的数据通常用于用数值的方式来衡量非数值的概念,比如说,满意度,幸福度等等,还有像成绩排名啊、比赛名次啊之类的。而连续尺度的数据就勿需解释了,常见的温度啊、体重啊、收入啊等等都(或严格、或近似)算是连续尺度的数据。
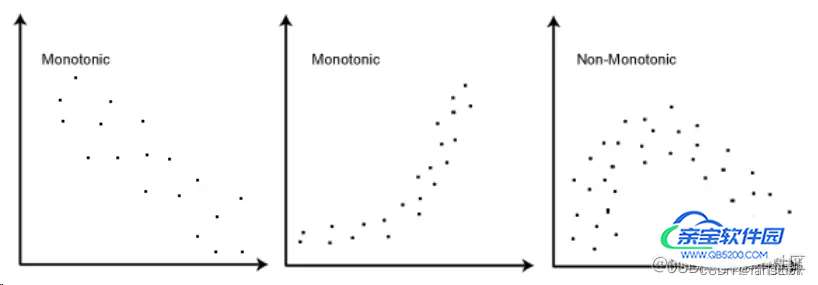
- 两个变量的数据之间应该遵循单调关系( monotonic relationship)。 简而言之就是,其中一个变量的值增大,另一个也增大,这个称为正相关;或者一个变量的值增大,另一个就变小,这个称为负相关。当然,这个单调关系是一个统计意义上的,或者说一种趋势上的,而非严格的单调。如下如所示。左图和中图都呈现一种近似单调的关系,而右图则不是,因为右图的左半部分和右半部分的趋势是相反的。
三、计算公式及代码示例
肯德尔系数有两个计算公式,一个称为Tau-c,另一个称为Tau-b。两者的区别是Tau-b可以处理有相同值的情况,即并列排位(tied ranks)。
1.Tau-a
from scipy.stats.stats import kendalltau import numpy as np import matplotlib.pyplot as plt dat1 = np.array([1,2,3,4,5,6,7,8]) dat2 = np.array([3,4,1,2,5,7,8,6]) fig,ax = plt.subplots() ax.scatter(dat1,dat2) kendalltau(dat1,dat2)
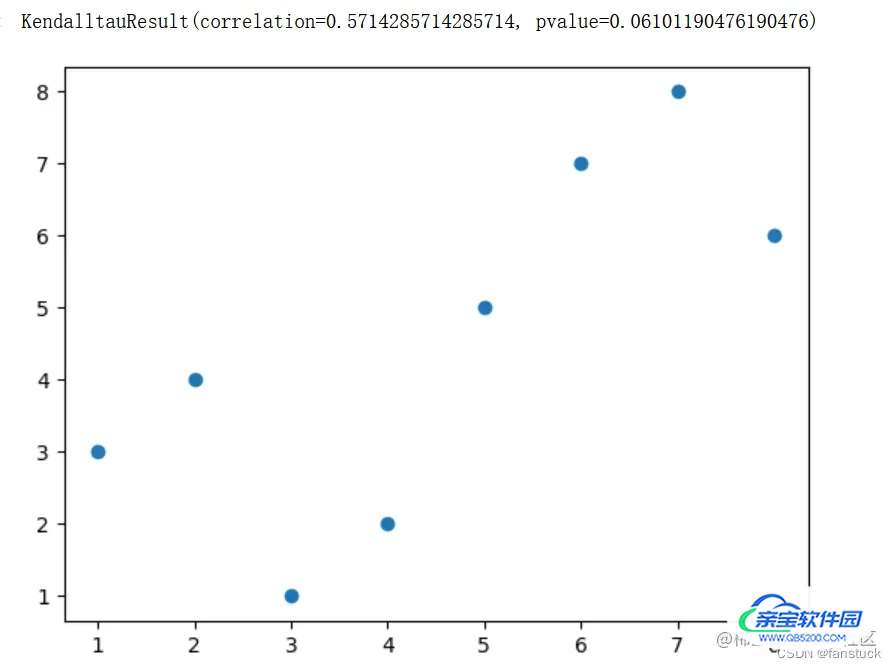
2.Tau-b
在以上Tau-a的计算中假定原始数据中不存在并列排位。当原始数据中存在并列排位时,则用以下公式能够给出更准确的分析结果。

代码是一致的只不过使用数学运算不一致,具体我不展开了,更多关于python肯德尔系数相关性的资料请关注其它相关文章!
加载全部内容