TypeScript实现十大排序算法之归并排序示例详解

时间:2023-03-20 coderwhy 人气:0

一. 归并排序的定义

归并排序（merge sort）是一种常见的排序算法：

它的基本思想是将待排序数组分成若干个子数组。
然后将相邻的子数组归并成一个有序数组。
最后再将这些有序数组归并（merge）成一个整体有序的数组。

这个算法最早出现在1945年，由约翰·冯·诺伊曼（John von Neumann）（又一个天才，现代计算机之父，冯·诺依曼结构、普林斯顿结构）首次提出。

当时他在为美国政府工作，研究原子弹的问题。
由于当时计算机，他在研究中提出了一种高效计算的方法，这个方法就是归并排序。

归并排序的基本思路是先将待排序数组递归地拆分成两个子数组，然后对每个子数组进行排序，最后将两个有序子数组合并成一个有序数组。

在实现中，我们可以使用“分治法”来完成这个过程，即将大问题分解成小问题来解决。

归并排序的算法复杂度为 O(nlogn)，是一种比较高效的排序算法，因此在实际应用中被广泛使用。

虽然归并排序看起来比较复杂，但是只要理解了基本思路，实现起来并不困难，而且它还是一个非常有趣的算法。

二. 归并排序的流程

归并排序是一种基于分治思想的排序算法，其基本思路可以分为三个步骤：

步骤一：分解（Divide）：归并排序使用递归算法来实现分解过程，具体实现中可以分为以下几个步骤：

如果待排序数组长度为1，认为这个数组已经有序，直接返回；
将待排序数组分成两个长度相等的子数组，分别对这两个子数组进行递归排序；
将两个排好序的子数组合并成一个有序数组，返回这个有序数组。

步骤二：合并（Merge）：合并过程中，需要比较每个子数组的元素并将它们有序地合并成一个新的数组：

可以使用两个指针 i 和 j 分别指向两个子数组的开头，比较它们的元素大小，并将小的元素插入到新的有序数组中。
如果其中一个子数组已经遍历完，就将另一个子数组的剩余部分直接插入到新的有序数组中。
最后返回这个有序数组。

步骤三：归并排序的递归终止条件：

归并排序使用递归算法来实现分解过程，当子数组的长度为1时，认为这个子数组已经有序，递归结束。

总体来看，归并排序的基本思路是分治法，分成子问题分别解决，然后将子问题的解合并成整体的解。

三. 归并排序的图解

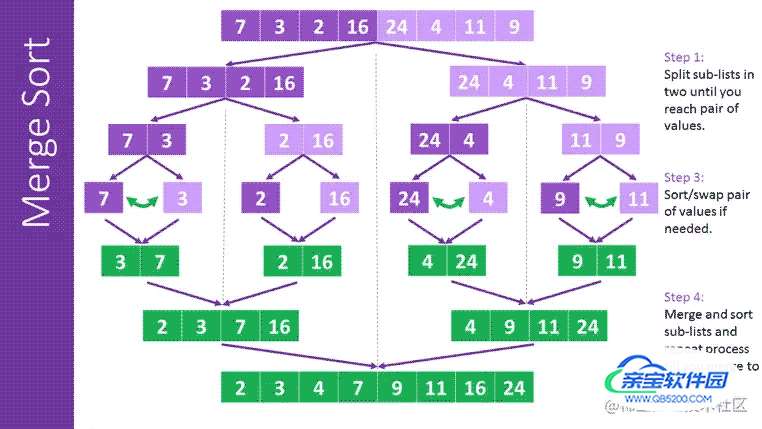
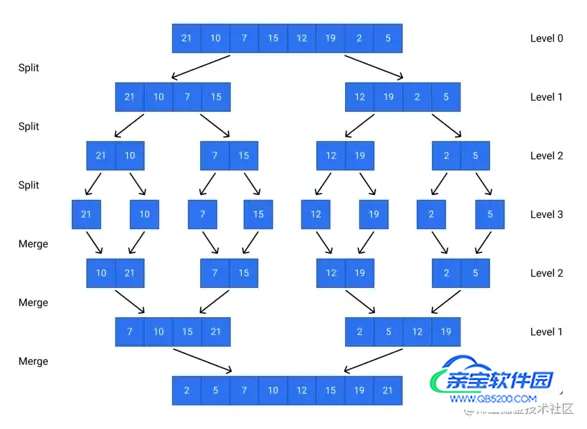
四. 归并排序的代码

下面是TypeScript实现的归并排序代码，带有详细的注释：

// 定义函数mergeSort，参数是待排序数组arr
function mergeSort(arr: number[]): number[] {
    // 计算数组长度
    const n = arr.length;
    // 如果数组长度小于等于1，则直接返回该数组
    if (n <= 1) {
        return arr;
    }
    // 计算中间位置
    const middle = Math.floor(n / 2);
    // 对左边的数组进行归并排序
    const left = mergeSort(arr.slice(0, middle));
    // 对右边的数组进行归并排序
    const right = mergeSort(arr.slice(middle));
    // 合并两个排好序的数组
    return merge(left, right);
}

// 定义函数merge，参数是两个排好序的数组left和right
function merge(left: number[], right: number[]): number[] {
    // 定义指针变量，分别指向两个数组的开头
    let i = 0, j = 0;
    // 定义一个空数组，用来存放合并后的数组
    const result = [];
    // 比较两个数组的第一个元素，将较小的放入result数组
    while (i < left.length && j < right.length) {
        if (left[i] < right[j]) {
            result.push(left[i++]);
        } else {
            result.push(right[j++]);
        }
    }
    // 将没有比较完的剩余元素放入result数组
    while (i < left.length) {
        result.push(left[i++]);
    }
    while (j < right.length) {
        result.push(right[j++]);
    }
    // 返回合并后的数组
    return result;
}


// 测试数据
const testArr = [5, 2, 9, 1, 5, 6];
// 调用插入排序函数
const sortedArr = mergeSort(testArr);
// 打印结果
console.log(sortedArr);

代码执行的过程：

mergeSort 函数实现归并排序的递归调用，在该函数内，如果数组的长度小于等于1，直接返回该数组。
如果数组的长度大于1，那么执行以下代码：
- 先计算数组的中点，并将数组分为左右两半。
- 递归调用左边和右边的数组，最终得到两个有序的数组。
merge 函数实现将两个有序的数组合并为一个有序的数组。

五. 归并排序的时间复杂度

复杂度的分析过程：

假设数组长度为 n，需要进行 logn 次归并操作；
每次归并操作需要 O(n) 的时间复杂度；
因此，归并排序的时间复杂度为 O(nlogn)。

最好情况： O(log n)

最好情况下，待排序数组已经是有序的了，那么每个子数组都只需要合并一次，即只需要进行一次归并操作。
因此，此时的时间复杂度是 O(log n)。

最坏情况： O(nlogn)

最坏情况下，待排序数组是逆序的，那么每个子数组都需要进行多次合并。

因此，此时的时间复杂度为 O(nlogn)。

平均情况： O(nlogn)

在平均情况下，我们假设待排序数组中任意两个元素都是等概率出现的。
此时，可以证明归并排序的时间复杂度为 O(nlogn)。

六. 归并排序的总结

归并排序是一种分治策略的排序算法，是利用分治的思想将一个大问题分成小问题，并在适当的地方合并它们以解决该问题的方法。

它是一种稳定的排序算法，时间复杂度为O(nlogn)。

归并排序使用了额外的空间，因此更适合处理大数据。

归并排序的基本流程是通过递归将数组分成两半，分别进行递归排序，最终再进行合并。
具体来说，将数组的中间元素作为分界点，分别对左右两边的数组进行排序，并在排序完成后进行合并。

归并排序的代码实现较为简单，但要注意关于递归函数和合并函数的实现。

归并排序是一种不需要过多研究的算法，适合于所有的排序场景。

加载全部内容