C++超详细分析优化排序算法之堆排序

时间:2023-03-20 36°熨斗的焦虑日记人气:0

堆排序，学习了整整一天才把这个排序彻底搞明白……

首先第一点，堆排序是直接选择排序的一种优化排序算法。由于直接排序算法的遍历次数过多，导致直接排序算法的时间复杂度为O(N^2)，不适合排大量数据，堆排序应运而生。

堆排序（Heap Sort）进行的改进是能够保存一部分在每次遍历整个数组找出最大（小）值、次大（小）值，主要利用的就是完全二叉树这种数据结构。（后面说是如何保存这些数据的）

堆排序最重要的知识点无非两个：

1、向下调整算法

2、堆的逻辑结构是一棵完全二叉树

先从定义开始学习：

向下调整算法：顾名思义就是从上到下进行数据的调整，可以将完全二叉树调整为最大堆与最小堆（这两种堆也同时被称为“大顶堆”和“小顶堆”）这种算法的前提是：根节点的左右两棵子树均以建成最大（小）堆。

最大堆：所有的父节点都大于子结点

最小堆：所有的父节点都小于子结点

完全二叉树：从上到下、从左到右依次排列的一种树（即从第一层到第n-1层都是满的，只有第n层不满且从左到右排列数据）

（以建小堆为例）看一种典型的示例：

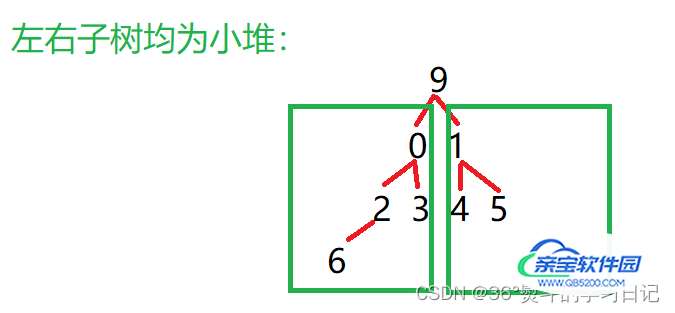
向下调整算法就是处理这种完全二叉树的一种算法，经过这种算法可将此数组建成最小堆。

先从根节点开始处理：

9 为父（根）节点，0，1都是其子节点，0 < 1；所以将0与9作一次交换；父节点同时下移至子节点，子节点变为新父节点的子节点：（p = parent, c = child）

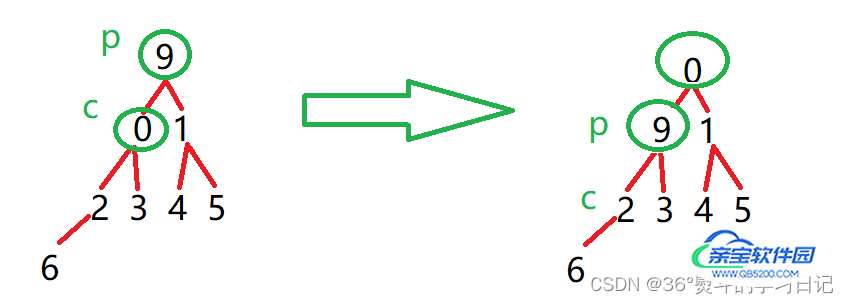
9 为父（根）节点，2，3都是其子节点，2 < 3；所以将2与9作一次交换；父节点同时下移至子节点，子节点变为新父节点的子节点：

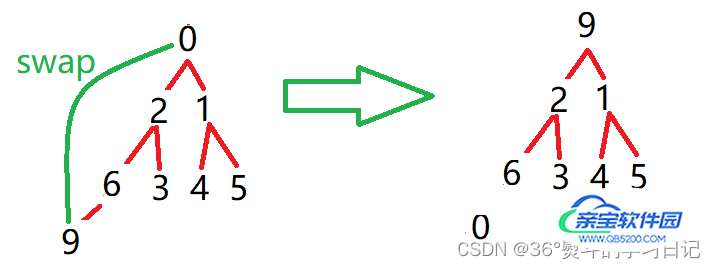
9 为父（根）节点，6 是其子节点，6< 9；所以将6与9作一次交换；父节点同时下移至子节点，子节点变为新父节点的子节点：

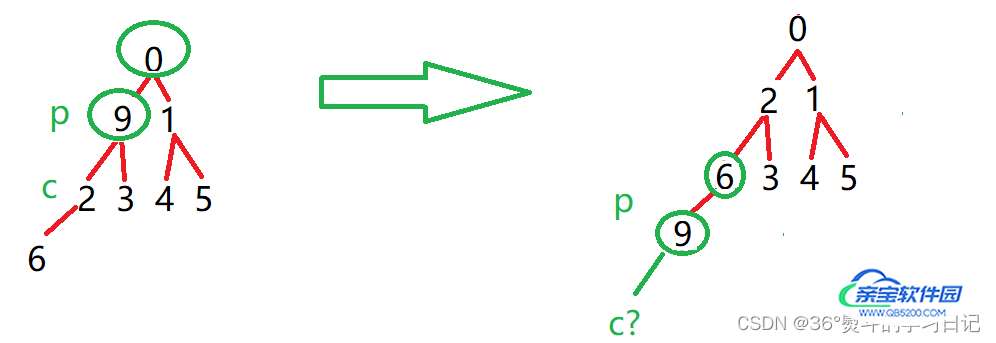
发现此时新的子节点已经越界，故停止向下调整；整个堆现已完成建堆成为最小堆！

这便是所谓的“向下调整算法”。

了解了以上知识后，还得知道父节点与子结点的表示方法：

leftchild = parent * 2 + 1;

rightchild = parent * 2 + 2;

parent = (leftchild - 1) /2;

下面代码实战：

//向下调整：
//根节点左右子树必须已经成堆
void AdjustDown(int a[], int n, int parent)
{
	int child = parent * 2 + 1;
	//左孩子不能越界
	while (child < n)
	{
		//如果只有左孩子，那就不用判断两个孩子的大小，直接判断左孩子和父亲的大小
		if (child + 1 < n && a[child + 1] > a[child])
		{
			child++;
		}
		//向下调整
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

简单的交换函数：

void Swap(int* a, int* b)
{
	int tmp = *a;
	*a = *b;
	*b = tmp;
}

堆排序的思想现在已经有了雏形：

将一个数组想象成堆，建堆，然后将堆顶最大（小）值置于堆底作为有序数据，这时会新形成一个堆，比之前的堆少一个数据，并且只有根节点的那棵小树未成堆，左右子树已形成大（小）堆，用一次向下调整算法即可将新堆再次建成最大（小）堆。

现在的问题是我们选择建一个最大堆还是最小堆呢？

我们不妨假设建了最小堆，也即上面我们刚刚构建好的堆：

不难发现这样是将最小值筛选出来，再向下调整，选出次小值，这样一来会得到降序的一个数组，反之，若使用最大堆，会得到一个升序的数组。

我们建大堆来得到一个升序数组，现有此无序数组：

//数组
int a[] = { 5,9,6,1,7,2,0,4,3,8 };
//元素个数
int n = (int)sizeof(a) / sizeof(a[0]);

第一步就是建堆：

我们会发现：这样“不听话”的数组显然不符合向下调整算法的前提条件，所以我们可以从这个数组中找能用这个算法的地方：从后向前去调整，最后一个叶子节点？一个数据，不需要调整；

最后一个父节点？他将会有0-2个子节点，而且只有这三个数据，不管怎么“不听话”，这个最小单位会满足“根的左右子树成堆”的这个条件，下一次再将这个父节点-1，即可实现对前一个父节点进行向下调整，循环此步骤直至真正的根节点，这时整个数组会被建成最大堆。

void HeapSort(int a[], int n)
{
    //建堆
	int parent = (n - 1 - 1) / 2;
	while (parent >= 0)
	{
		AdjustDown(a, n, parent);
		parent--;
	}
}

第二步就是排序：

建成堆后，我们需要进行数据的交换形成有序数据区。

void HeapSort(int a[], int n)
{
    //建堆
	int parent = (n - 1 - 1) / 2;
	while (parent >= 0)
	{
		AdjustDown(a, n, parent);
		parent--;
	}
	//已经成最大堆,不用再从最后一个父节点建堆
	//每次只用改变根节点的堆（根左右堆已为最大堆）
	int end = n - 1;
	while (end > 0)
	{
		Swap(&a[0], &a[end]);
		AdjustDown(a, end, 0);
		end--;
	}
}

堆排序完毕！

整个代码分享：

#include <stdio.h>
void Swap(int* a, int* b)
{
	int tmp = *a;
	*a = *b;
	*b = tmp;
}
//向下调整：
//根节点左右子树必须已经成堆
void AdjustDown(int a[], int n, int parent)
{
	int child = parent * 2 + 1;
	//左孩子不能越界
	while (child < n)
	{
		//如果只有左孩子，那就不用判断两个孩子的大小，直接判断左孩子和父亲的大小
		if (child + 1 < n && a[child + 1] > a[child])
		{
			child++;
		}
		//向下调整
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}
void HeapSort(int a[], int n)
{
	int parent = (n - 1 - 1) / 2;
	while (parent >= 0)
	{
		AdjustDown(a, n, parent);
		parent--;
	}
	//已经成最大堆,不用再从最后一个父节点建堆
	//每次只用改变根节点的堆（根左右堆已为最大堆）
	int end = n - 1;
	while (end > 0)
	{
		Swap(&a[0], &a[end]);
		AdjustDown(a, end, 0);
		end--;
	}
}
void print(int* a, int n)
{
	int i = 0;
	for (i = 0; i < n; i++)
	{
		printf("%d ", a[i]);
	}
	printf("\n");
}
int main()
{
	int a[] = { 5,9,6,1,7,2,0,4,3,8 };
	int n = (int)sizeof(a) / sizeof(a[0]);
	HeapSort(a, n);
	print(a, n);
	return 0;
}

加载全部内容