go语言题解LeetCode1128等价多米诺骨牌对的数量

时间:2023-02-03 刘09k11 人气:0

题目描述

给你一个由一些多米诺骨牌组成的列表 dominoes。

如果其中某一张多米诺骨牌可以通过旋转 0 度或 180 度得到另一张多米诺骨牌，我们就认为这两张牌是等价的。

形式上，dominoes[i] = [a, b] 和 dominoes[j] = [c, d] 等价的前提是 a==c 且 b==d，或是 a==d 且 b==c。

在 0 <= i < j < dominoes.length 的前提下，找出满足 dominoes[i] 和 dominoes[j] 等价的骨牌对 (i, j) 的数量。

示例：

输入：dominoes = [[1,2],[2,1],[3,4],[5,6]]
输出：1

提示：

1 <= dominoes.length <= 40000

1 <= dominoes[i][j] <= 9

思路分析

这道题想到的是用关联容器来解决，其中用无序容器更好做。

分析题目的条件可以等价为比较两个子vector里面的最大值和最小值（比较vec1和vec1的最大值，比较vec1和vec2的最小值）所以KEY 可以设为minNUM maxNUM

在桶里面将存放{minNUM,maxNUM}

遍历整个dominoes 求出每个子vector里的最大值maxNUM，最小值minNUM 形成KEY ｛minNUM,maxNUM｝然后在桶里查找这个KEY ｛minNUM,maxNUM｝，如果没找到，则将这个KEY存入桶里并递增计数1 ,找到了就在对应的KEY 递增计数1，并且更新count

AC 代码

struct KEY
{
    int minNum;
    int maxNum;
    KEY(int f,int s):minNum(f),maxNum(s){}
};
struct HashFunc
{
    size_t operator()(const KEY& key) const
    {
        return ((hash<int>()(key.minNum) ^ (hash<int>()(key.maxNum) << 1)) >> 1);
    }
};
struct EqualKey
{
	bool operator () (const KEY &lhs, const KEY &rhs) const
	{
		return lhs.minNum  == rhs.minNum && lhs.maxNum == rhs.maxNum;
	}
};
class Solution {
public:
    int numEquivDominoPairs(vector<vector<int>>& dominoes) {
        unordered_map<KEY,int,HashFunc,EqualKey> um;
        int count = 0;
        int maxNum = 0,minNum = 0;
        for(auto &n : dominoes)
        {
            minNum = min(n[0],n[1]);
            maxNum = max(n[0],n[1]);
            if(um.find({minNum,maxNum}) != um.end())
            {
                count += um[{minNum,maxNum}];
                um[{minNum,maxNum}]++;
            }
            else
            {
                um[{minNum,maxNum}]++;
            }
        }
        return count;
    }
};

偷懒解法

思路：

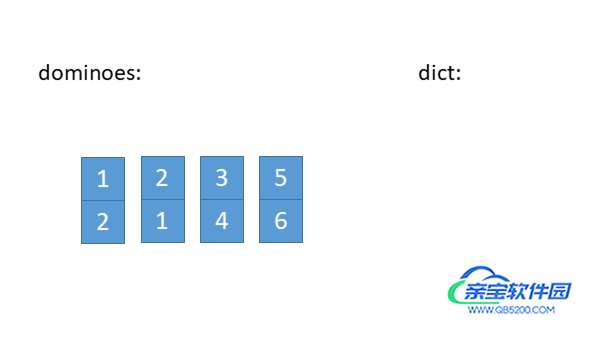
把每个多米诺骨牌翻成小的数字在上，大的数字在下的情况，这样可以使相同的多米诺骨牌的状态也相同，便于统计数目。然后用哈希字典来统计每种多米诺骨牌的个数，最后遍历每种骨牌，用组合数学 n * (n - 1) // 2 求每种骨牌成对的数目，将其累加得到最后结果。

图解：

代码：

class Solution:
    def numEquivDominoPairs(self, dominoes: List[List[int]]) -> int:
        ans = 0
        d = dict()
        for d1, d2 in dominoes:
            # 排序后加入字典
            index = tuple(sorted((d1, d2)))
            if index in d:
                d[index] += 1
            else:
                d[index] = 1
        # 计算答案
        for i in d:
            ans += d[i] * (d[i] - 1) // 2
        return ans

哈希表+元素转换

解题思路

将每个元素 [a,b] 转换为 ab，降成一维数组以后就可以利用哈希表统计频数，因为元素翻转相同或者不反转相同都是等价的，所以可以利用高斯求和公式计算每个频数超过1的元素的数量，再将所以数量相加即为结果。

代码

class Solution:
    def numEquivDominoPairs(self, dominoes: List[List[int]]) -> int:
        dominoes_new = []
        for i in dominoes:
            a = i[0]
            b = i[1]
            if a > b:
                a, b = b, a
            dominoes_new.append(a*10+b)
        Hash = {}
        for j in dominoes_new:
            Hash[j] = Hash.get(j, 0) + 1
        res = 0
        for key in Hash.keys():
            n = Hash[key]
            res += n*(n-1)//2
        return res

复杂度分析

时间复杂度：O(N)

空间复杂度：O(N)

加载全部内容