Pytorch中torch.argmax()函数使用及说明

torch.argmax()函数解析

1. 官网链接

torch.argmax()，如下图所示：

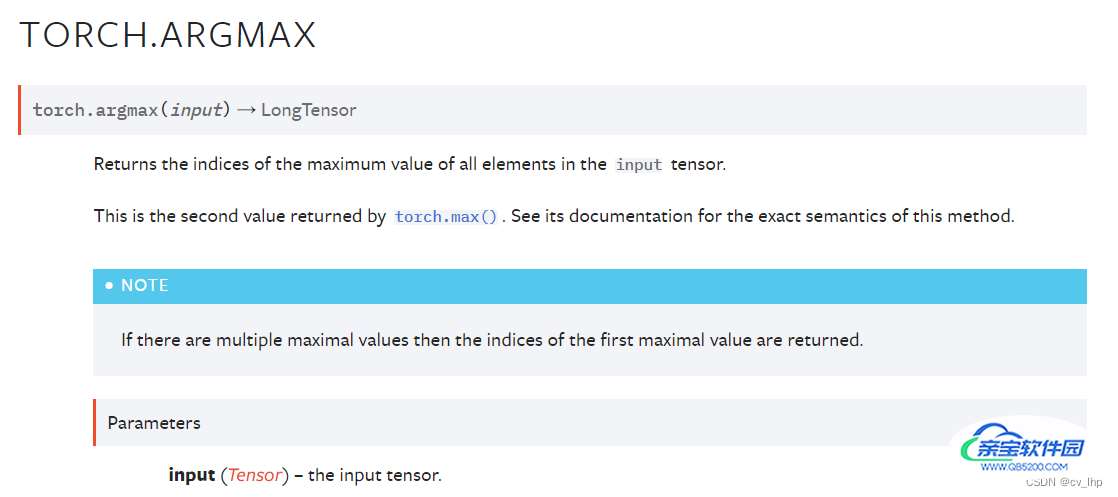
2. torch.argmax(input)函数解析

torch.argmax(input) → LongTensor

将输入input张量，无论有几维，首先将其reshape排列成一个一维向量，然后找出这个一维向量里面最大值的索引。

3. 代码举例

import torch
x = torch.randn(3,4)
y = torch.argmax(x)#对应于x中最大元素的索引值
x,y

输出结果如下：

import torch
x = torch.randn(3,4)
y = torch.argmax(x)#对应于x中最大元素的索引值
x,y

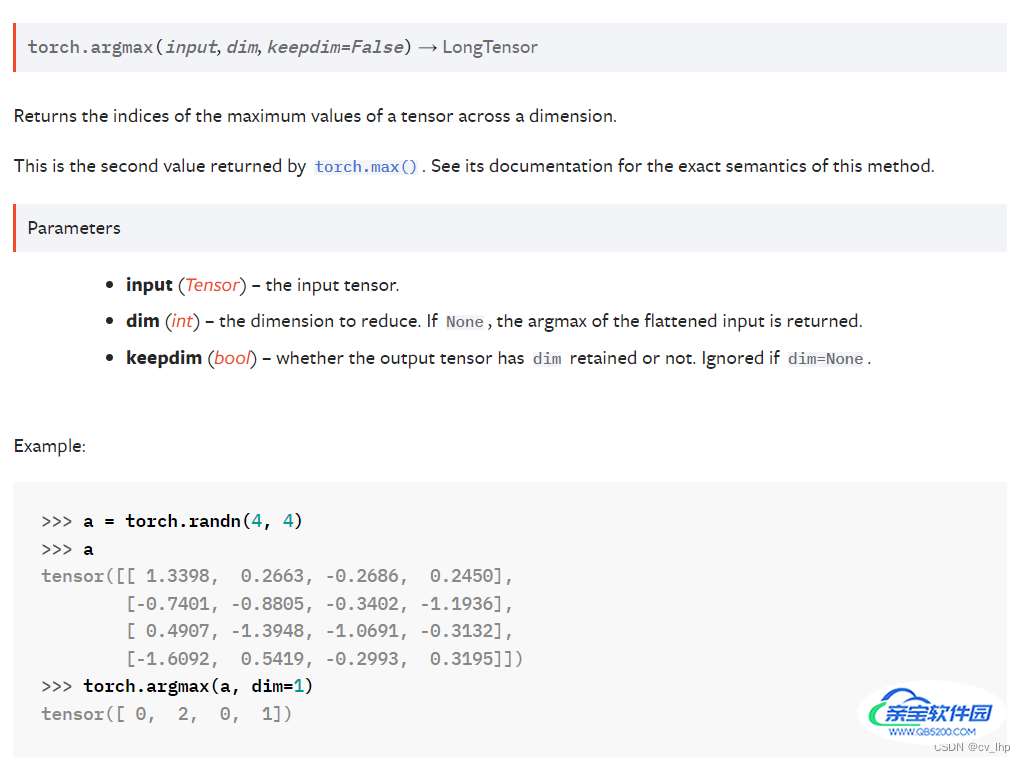
4. torch.argmax(input,dim) 函数解析

torch.argmax(input, dim, keepdim=False) → LongTensor

函数返回其他所有维在这个维度上面张量最大值的索引。

torch.argmax()函数中dim表示该维度会消失，可以理解为最终结果该维度大小是1，表示将该维度压缩成维度大小为1。

举例理解：

对于一个维度为(d0,d1) 的矩阵来说，dim=1表示求每一行中最大数的在该行中的列号，最后得到的就是一个维度为(d0,1) 的二维矩阵，最终列这一维度大小为1就要消失了，最终结果变成一维张量(d0)；
dim=0表示求每一列中最大数的在该列中的行号，最后我们得到的就是一个维度为(1，d1) 的二维矩阵，结果行这一维度大小为1就要消失了，最终结果变成一维张量(d1)。

因此，我们想要求每一行最大的列标号，我们就要指定dim=1，表示我们不要列了，保留行的size就可以了。

假如我们想求每一列的最大行标，就可以指定dim=0，表示我们不要行了，求出每一列的最大值的下标，最后得到（1,d1）的一维矩阵。

5. 代码举例

5.1 输入二维张量torch.Size([3, 4])，dim=0表示将dim=0这个维度大小由3压缩成1，然后找到dim=0这三个值中最大值的索引，这个索引表示dim=0行索引标号，结果张量维度变为torch.Size([4])。

import torch
x = torch.randn(3,4)
y = torch.argmax(x,dim=0)#dim=0表示将dim=0这个维度大小由3压缩成1，然后找到dim=0这三个值中最大值的索引，这个索引表示dim=0行索引标号
x,x.shape,y,y.shape

输出结果如下：

(tensor([[ 2.6347,  0.6456, -1.0461, -1.5154],
         [-1.3955, -1.2618, -0.5886, -0.5947],
         [-1.5272, -2.0960,  0.9428, -0.9532]]),
 torch.Size([3, 4]),
 tensor([0, 0, 2, 1]),
 torch.Size([4]))

5.2 输入二维张量torch.Size([3, 4])，dim=1表示将dim=1这个维度大小由4压缩成1，然后找到dim=1这四个值中最大值的索引，这个索引表示dim=1列索引标号，结果张量维度变为torch.Size([3])。

import torch
x = torch.randn(3,4)
y = torch.argmax(x,dim=1)#dim=1表示将dim=1这个维度大小由4压缩成1，然后找到dim=1这四个值中最大值的索引，这个索引表示dim=1列索引标号
x,x.shape,y,y.shape

输出结果如下：

(tensor([[ 0.1549,  0.4331,  0.3575,  1.1077],
         [ 2.0233,  2.0085, -0.6101, -1.8547],
         [-0.5101, -0.4052,  0.3458, -0.7802]]),
 torch.Size([3, 4]),
 tensor([3, 0, 2]),
 torch.Size([3]))

5.3 输入三维张量torch.Size([2, 3, 4])，dim=0表示将dim=0这个维度大小由2压缩成1，然后找到dim=0这两个值中最大值的索引，这个索引表示dim=0维索引标号。

dim=0,即将第一个维度消除，也就是将两个[34]矩阵只保留一个，因此要在两组中作比较，即将上下两个[34]的矩阵分别在对应的位置上比较大小，结果矩阵张量维度变为torch.Size([3, 4])。

import torch
x = torch.randn(2,3,4)
y = torch.argmax(x,dim=0)#dim=0表示将dim=0这个维度大小由2压缩成1，然后找到dim=0这两个值中最大值的索引，这个索引表示dim=0维索引标号
x,x.shape,y,y.shape

输出结果如下：

(tensor([[[-1.4430,  0.0306, -1.0396,  0.1219],
          [ 0.1016,  0.0889,  0.8005,  0.3320],
          [-1.0518, -1.4526, -0.4586, -0.1474]],
 
         [[ 1.2274,  1.5806,  0.5444, -0.3088],
          [-0.8672,  0.3843,  1.2377,  2.1596],
          [ 0.0671,  0.0847,  0.5607, -0.7492]]]),
 torch.Size([2, 3, 4]),
 tensor([[1, 1, 1, 0],
         [0, 1, 1, 1],
         [1, 1, 1, 0]]),
 torch.Size([3, 4]))

5.4 输入三维张量torch.Size([2, 3, 4])，dim=1表示将dim=1这个维度大小由3压缩成1，然后找到dim=1这三个值中最大值的索引，这个索引表示dim=1维索引标号。

dim=1，即将第二个维度消除（纵向压缩成一维），结果矩阵张量维度变为torch.Size([2, 4])。

import torch
x = torch.randn(2,3,4)
y = torch.argmax(x,dim=1)#dim=1表示将dim=1这个维度大小由3压缩成1，然后找到dim=1这三个值中最大值的索引，这个索引表示dim=1维索引标号
x,x.shape,y,y.shape

输出结果如下：

(tensor([[[-1.7136,  0.5528,  0.5171,  1.2978],
          [ 1.0250, -0.2687,  0.6727, -0.2013],
          [ 0.1366, -1.0563,  0.1965,  1.5303]],
 
         [[-0.0048,  1.6265, -1.0341, -0.3994],
          [ 1.5536,  0.9739, -0.0913,  0.0889],
          [-0.6703, -0.9099, -0.6400, -0.1807]]]),
 torch.Size([2, 3, 4]),
 tensor([[1, 0, 1, 2],
         [1, 0, 1, 1]]),
 torch.Size([2, 4]))

5.5 输入三维张量torch.Size([2, 3, 4])，dim=2表示将dim=2这个维度大小由4压缩成1，然后找到dim=2这四个值中最大值的索引，这个索引表示dim=2维索引标号。dim=2,即将第三个维度消除（横向压缩成一维），结果矩阵张量维度变为torch.Size([2, 3])。

import torch
x = torch.randn(2,3,4)
y = torch.argmax(x,dim=2)#dim=2表示将dim=2这个维度大小由4压缩成1，然后找到dim=2这四个值中最大值的索引，这个索引表示dim=2维索引标号
x,x.shape,y,y.shape

输出结果如下：

(tensor([[[-0.3493,  0.8838,  0.5876, -0.3967],
          [-1.5795,  2.6964,  0.7266,  0.3517],
          [-0.6949, -1.4385, -0.0993,  0.1679]],
 
         [[-0.4924, -0.8955,  0.5511,  0.6287],
          [ 0.2338, -0.5787, -0.2081, -1.3032],
          [ 0.6429,  0.0949,  0.3319, -0.8551]]]),
 torch.Size([2, 3, 4]),
 tensor([[1, 1, 3],
         [3, 0, 0]]),
 torch.Size([2, 3]))

总结

以上为个人经验，希望能给大家一个参考，也希望大家多多支持。