Python图像锐化与边缘检测之Scharr,Canny,LOG算子详解

时间:2022-12-24 Eastmount 人气:0

一.Scharr算子

由于Sobel算子在计算相对较小的核的时候，其近似计算导数的精度比较低，比如一个3×3的Sobel算子，当梯度角度接近水平或垂直方向时，其不精确性就越发明显。Scharr算子同Sobel算子的速度一样快，但是准确率更高，尤其是计算较小核的情景，所以利用3×3滤波器实现图像边缘提取更推荐使用Scharr算子。

Scharr算子又称为Scharr滤波器，也是计算x或y方向上的图像差分，在OpenCV中主要是配合Sobel算子的运算而存在的，其滤波器的滤波系数如下：

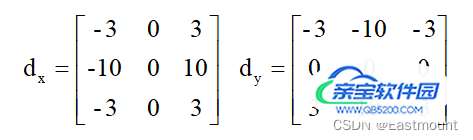
Scharr算子的函数原型如下所示，和Sobel算子几乎一致，只是没有ksize参数。

dst = Scharr(src, ddepth, dx, dy[, dst[, scale[, delta[, borderType]]]]])

– src表示输入图像
– dst表示输出的边缘图，其大小和通道数与输入图像相同
– ddepth表示目标图像所需的深度，针对不同的输入图像，输出目标图像有不同的深度
– dx表示x方向上的差分阶数，取值1或 0
– dy表示y方向上的差分阶数，取值1或0
– scale表示缩放导数的比例常数，默认情况下没有伸缩系数
– delta表示将结果存入目标图像之前，添加到结果中的可选增量值
– borderType表示边框模式，更多详细信息查阅BorderTypes

Scharr算子的实现代码如下所示。

# -*- coding: utf-8 -*-
# By:Eastmount
import cv2  
import numpy as np  
import matplotlib.pyplot as plt
 
#读取图像
img = cv2.imread('luo.png')
lenna_img = cv2.cvtColor(img,cv2.COLOR_BGR2RGB)

#灰度化处理图像
grayImage = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
 
# Scharr算子
x = cv2.Scharr(grayImage, cv2.CV_32F, 1, 0) #X方向
y = cv2.Scharr(grayImage, cv2.CV_32F, 0, 1) #Y方向
absX = cv2.convertScaleAbs(x)       
absY = cv2.convertScaleAbs(y)
Scharr = cv2.addWeighted(absX, 0.5, absY, 0.5, 0)

#用来正常显示中文标签
plt.rcParams['font.sans-serif']=['SimHei']

#显示图形
titles = ['原始图像', 'Scharr算子']  
images = [lenna_img, Scharr]  
for i in range(2):  
   plt.subplot(1,2,i+1), plt.imshow(images[i], 'gray')  
   plt.title(titles[i])  
   plt.xticks([]),plt.yticks([])  
plt.show()

其运行结果如图1所示：

二.Cann算子

John F.Canny于1986年发明了一个多级边缘检测算法——Canny边缘检测算子，并创立了边缘检测计算理论（Computational theory of edge detection），该理论有效地解释了这项技术的工作理论。

边缘检测通常是在保留原有图像属性的情况下，对图像数据规模进行缩减，提取图像边缘轮廓的处理方式。Canny算法是一种被广泛应用于边缘检测的标准算法，其目标是找到一个最优的边缘检测解或找寻一幅图像中灰度强度变化最强的位置。最优边缘检测主要通过低错误率、高定位性和最小响应三个标准进行评价。Canny算子的实现步骤如下：

第一步，使用高斯平滑（如公式2所示）去除噪声。

第二步，按照Sobel滤波器步骤计算梯度幅值和方向，寻找图像的强度梯度。先将卷积模板分别作用x和y方向，再计算梯度幅值和方向，其公式如下所示。梯度方向一般取0度、45度、90度和135度四个方向。

第三步，通过非极大值抑制（Non-maximum Suppression）过滤掉非边缘像素，将模糊的边界变得清晰。该过程保留了每个像素点上梯度强度的极大值，过滤掉其他的值。对于每个像素点，它进行如下操作：

将其梯度方向近似为以下值中的一个，包括0、45、90、135、180、225、270和315，即表示上下左右和45度方向；
比较该像素点和其梯度正负方向的像素点的梯度强度，如果该像素点梯度强度最大则保留，否则抑制（删除，即置为0）。其处理后效果如图2所示，左边表示梯度值，右边表示非极大值抑制处理后的边缘。

第四步，利用双阈值方法来确定潜在的边界。经过非极大抑制后图像中仍然有很多噪声点，此时需要通过双阈值技术处理，即设定一个阈值上界和阈值下界。图像中的像素点如果大于阈值上界则认为必然是边界（称为强边界，strong edge），小于阈值下界则认为必然不是边界，两者之间的则认为是候选项（称为弱边界，weak edge）。经过双阈值处理的图像如图3所示，左边为非极大值抑制处理后的边缘，右边为双阈值技术处理的效果图。

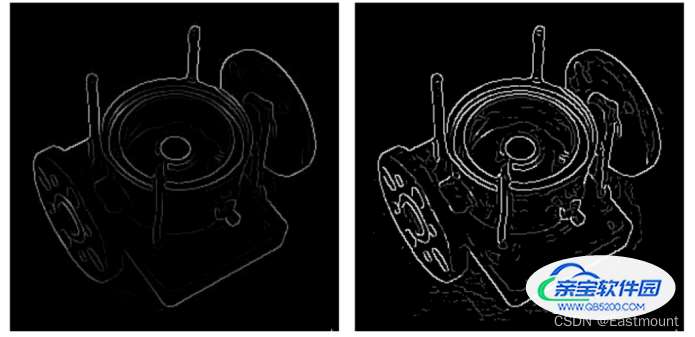
第五步，利用滞后技术来跟踪边界。若某一像素位置和强边界相连的弱边界认为是边界，其他的弱边界则被删除。
在OpenCV中，Canny()函数原型如下所示：

edges = Canny(image, threshold1, threshold2[, edges[, apertureSize[, L2gradient]]])

– image表示输入图像
– edges表示输出的边缘图，其大小和类型与输入图像相同
– threshold1表示第一个滞后性阈值
– threshold2表示第二个滞后性阈值
– apertureSize表示应用Sobel算子的孔径大小，其默认值为3
– L2gradient表示一个计算图像梯度幅值的标识，默认值为false

Canny算子的边缘提取实现代码如下所示：

# -*- coding: utf-8 -*-
# By:Eastmount
import cv2  
import numpy as np  
import matplotlib.pyplot as plt
 
#读取图像
img = cv2.imread('luo.png')
lenna_img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)

#灰度化处理图像
grayImage = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)

#高斯滤波降噪
gaussian = cv2.GaussianBlur(grayImage, (3,3), 0)
 
#Canny算子
Canny = cv2.Canny(gaussian, 50, 150) 

#用来正常显示中文标签
plt.rcParams['font.sans-serif']=['SimHei']

#显示图形
titles = ['原始图像', 'Canny算子']  
images = [lenna_img, Canny]  
for i in range(2):  
   plt.subplot(1,2,i+1), plt.imshow(images[i], 'gray')  
   plt.title(titles[i])  
   plt.xticks([]),plt.yticks([])  
plt.show()

其运行结果如图4所示：

三.LOG算子

LOG（Laplacian of Gaussian）边缘检测算子是David Courtnay Marr和Ellen Hildreth在1980年共同提出的，也称为Marr & Hildreth算子，它根据图像的信噪比来求检测边缘的最优滤波器。该算法首先对图像做高斯滤波，然后再求其拉普拉斯（Laplacian）二阶导数，根据二阶导数的过零点来检测图像的边界，即通过检测滤波结果的零交叉（Zero crossings）来获得图像或物体的边缘。

LOG算子综合考虑了对噪声的抑制和对边缘的检测两个方面，并且把Gauss平滑滤波器和Laplacian锐化滤波器结合了起来，先平滑掉噪声，再进行边缘检测，所以效果会更好。该算子与视觉生理中的数学模型相似，因此在图像处理领域中得到了广泛的应用。它具有抗干扰能力强，边界定位精度高，边缘连续性好，能有效提取对比度弱的边界等特点。

常见的LOG算子是5×5模板，如下所示：

由于LOG算子到中心的距离与位置加权系数的关系曲线像墨西哥草帽的剖面，所以LOG算子也叫墨西哥草帽滤波器，如图5所示。

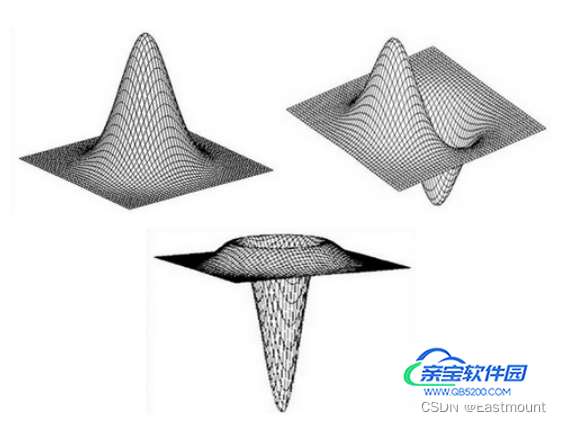
LOG算子的边缘提取实现代码如下所示：

# -*- coding: utf-8 -*-
# By:Eastmount
import cv2  
import numpy as np  
import matplotlib.pyplot as plt
 
#读取图像
img = cv2.imread('luo.png')
lenna_img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)

#灰度化处理图像
grayImage = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)

#先通过高斯滤波降噪
gaussian = cv2.GaussianBlur(grayImage, (3,3), 0)
 
#再通过拉普拉斯算子做边缘检测
dst = cv2.Laplacian(gaussian, cv2.CV_16S, ksize = 3)
LOG = cv2.convertScaleAbs(dst)

#用来正常显示中文标签
plt.rcParams['font.sans-serif']=['SimHei']

#显示图形
titles = ['原始图像', 'LOG算子']  
images = [lenna_img, LOG]  
for i in range(2):  
   plt.subplot(1,2,i+1), plt.imshow(images[i], 'gray')  
   plt.title(titles[i])  
   plt.xticks([]),plt.yticks([])  
plt.show()

其运行结果如图6所示：

四.总结

该系列文章主要通过Roberts算子、Prewitt算子、Sobel算子、Laplacian算子、Scharr算子、Canny算子和LOG算子实现图像锐化和边缘检测，有效地提取了图像的轮廓，并进行了详细地实验处理。

加载全部内容