Python使用穷举法求两个数的最大公约数问题
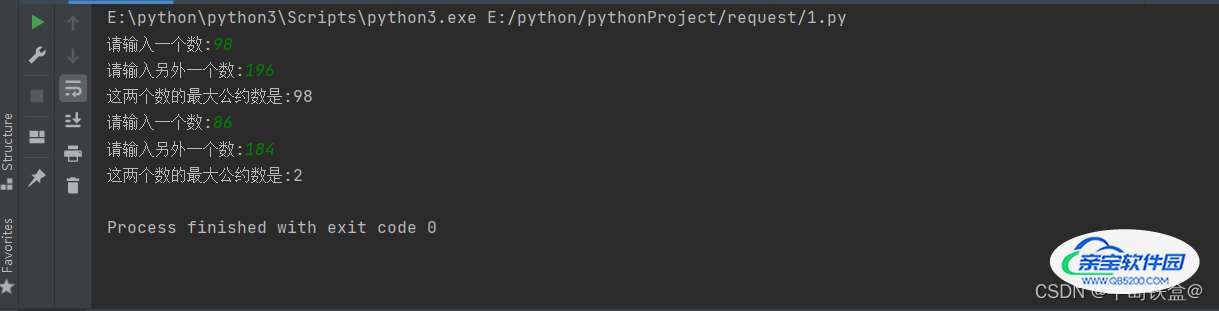
半岛铁盒@ 人气:0使用穷举法求两个数的最大公约数

for m in range (0,2):
a = int(input("请输入一个数:"))
b = int(input("请输入另外一个数:"))
#判断num1与num2的大小
if a > b:
#获取最小值
min = b
else:
#获取最小值
min = a
for i in range(min+1,0,-1): #倒序
#满足公因数的条件:
if (a % i == 0) and (b % i == 0):
c = i
break
print('这两个数的最大公约数是:%d '%c)
穷举法求N个数的最大公约数和最小公倍数
基本要求
求N个数的最大公约数和最小公倍数。用C或C++或java或python语言实现程序解决问题。
提高要求
思考一个“求公约数”和“求公倍数”之类问题的“逆问题”,这个问题是这样的:已知正整数a0,a1,b0,b1,设某未知正整数x满足:
- 1、x和a0的最大公约数是a1;
- 2、x和b0的最小公倍数是b1。
Hankson的“逆问题”就是求出满足条件的正整数x。但稍加思索之后,他发现这样的x并不唯一,甚至可能不存在。因此他转而开始考虑如何求解满足条件的x的个数。
输入格式
- 输入第一行为一个正整数n,表示有n组输入数据。接下来的n行每行一组输入数据,为四个正整数a0,a1,b0,b1,每两个整数之间用一个空格隔开。输入数据保证a0能被a1整除,b1能被b0整除。
输出格式
- 输出共n行。每组输入数据的输出结果占一行,为一个整数。
- 对于每组数据:若不存在这样的x,请输出0;
- 若存在这样的x,请输出满足条件的x的个数;
样例输入
2
41 1 96 288
95 1 37 1776
算法设计思路
本程序先用穷举法计算两个数的最大公约数或最小公倍数。从两个数中较小数开始由大到小列举,直到找到公约数立即中断列举,得到的公约数便是最大公约数 。
①定义1:对两个正整数a,b如果能在区间[a,0]或[b,0]内能找到一个整数temp能同时被a和b所整除,则temp即为最大公约数。
②定义2:对两个正整数a,b,如果若干个a之和或b之和能被b所整除或能被a所整除,则该和数即为所求的最小公倍数。
#include<stdio.h>
#define N 1000 /*自定义数组长度*/
int input(int t[])
{
int i,n;
int k=1;
printf("Please input the count of numbers(n>=2):"); /*输入计算值的个数*/
scanf("%d",&n);
while(k)
{
printf("Please input numbers:\n"); /*输入所算值*/
for(i=0;i<n;i++)
{
scanf("%d",&t[i]);
}
k=exper(t,n);
}
return n;
}
int exper(int t[],int n) /*验证函数*/
{
int i;
for(i=0;i<n;i++)
{
if(!t[i])
{
printf("error(输入为0)\n");
return 1;
}
}
return 0;
}
int divisor (int a,int b) /*自定义函数求两数的最大公约数*/
{
int temp; /*定义义整型变量*/
temp=(a>b)?b:a; /*采种条件运算表达式求出两个数中的最小值*/
while(temp>0)
{
if (a%temp==0&&b%temp==0) /*只要找到一个数能同时被a,b所整除,则中止循环*/
break;
temp--; /*如不满足if条件则变量自减,直到能被a,b所整除*/
}
return (temp); /*返回满足条件的数到主调函数处*/
}
int Gcd(int t[],int n)
{
int i;
int c=t[0];
for(i=1;i<n;i++)
{
c=divisor(c,t[i]); /*求N个数的最大公约数*/
}
return c;
}
int multiple (int a,int b)
{
int p,q,temp;
p=(a>b)?a:b; /*求两个数中的最大值*/
q=(a>b)?b:a; /*求两个数中的最小值*/
temp=p; /*最大值赋给p为变量自增作准备*/
while(1)
{
if(p%q==0)
break; /*只要找到变量的和数能被a或b所整除,则中止循环*/
p+=temp; /*如果条件不满足则变量自身相加*/
}
return (p);
}
int Mul(int t[],int n)
{
int i;
int s=t[0];
for(i=0;i<n;i++)
{
s=multiple(s,t[i]); /*求N个数的最小公倍数*/
}
return s;
}
int main()
{
int t[N];
int n;
int flag=1;
while(flag)
{
n=input(t);
printf("The higest common divisor is %d\n",Gcd(t,n)); /*输出最大公约数*/
printf("The lowest common multiple is %d\n",Mul(t,n));/*输出最小公倍数*/
printf("retreat:press 0\ncontiune:press 1");
scanf("%d",&flag);
}
return 0;
}测试截屏
输入数据正确时:
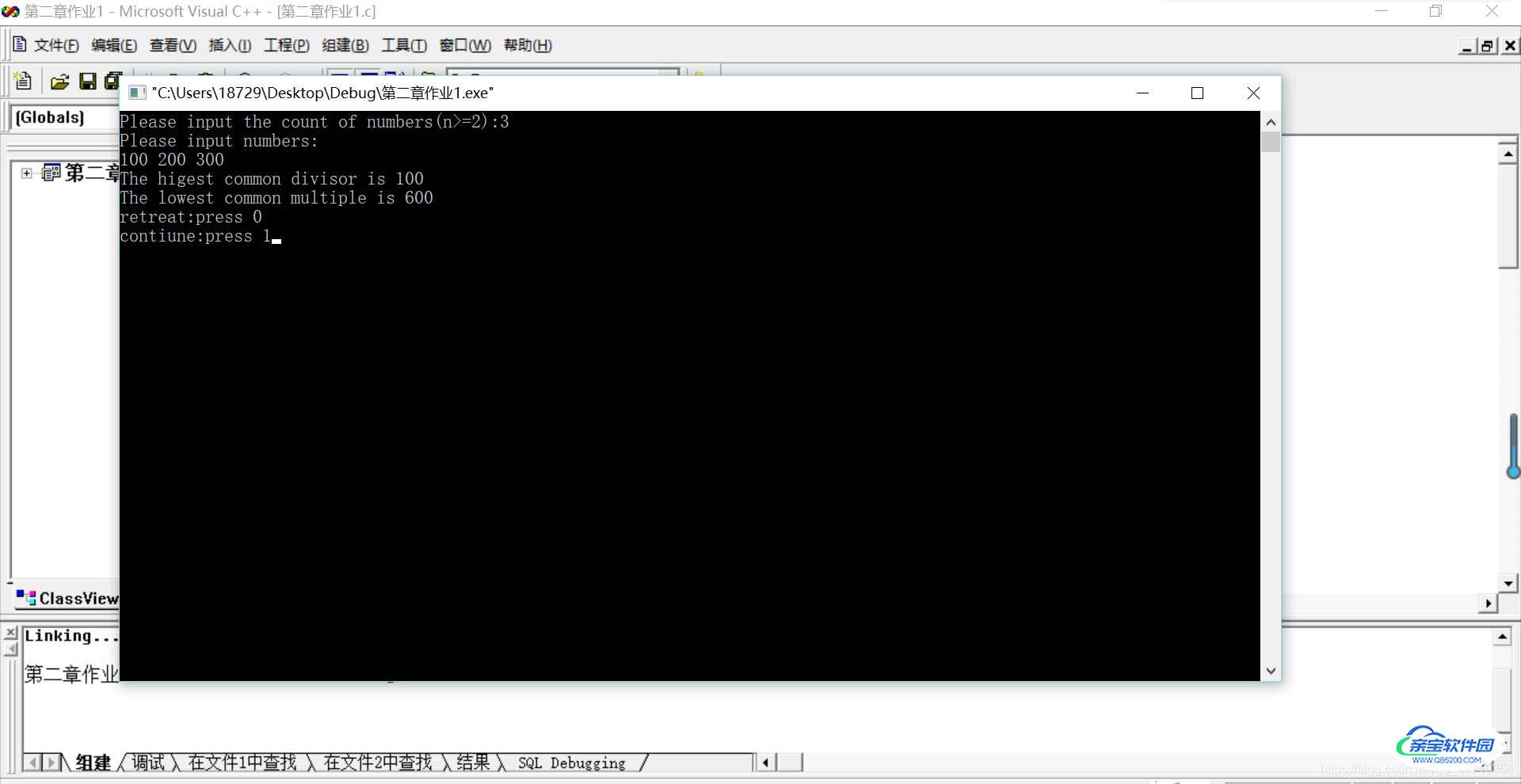
输入数据有0时会提示错误,计算完成后可以退出和继续:
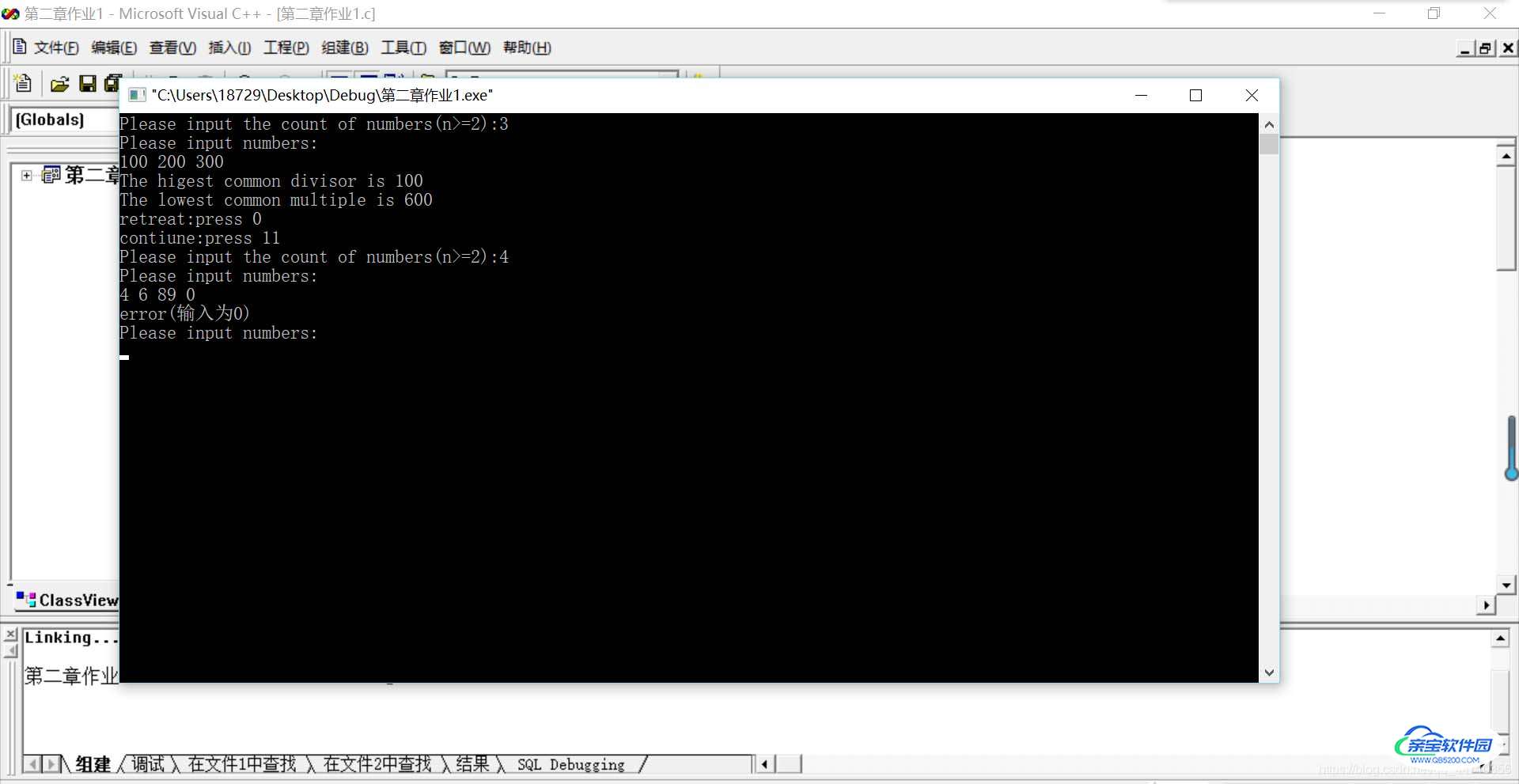
总结
求N个数的最大公约数和最小公倍数的可以联系上机作业:用四种方法求两个数最大公约数和最小公倍数,像这种思考方式可以用于以后的解决问题中。
在完成基本要求中,程序完成比较顺利。提高要求仔细读了几遍,明白了题意,寻找满足x的个数,这就要用到循环和计数器一个个去找,但此要求最终没能完成,在对x的求解过程仍有问题。
以上为个人经验,希望能给大家一个参考,也希望大家多多支持。
加载全部内容