Python CNN卷积神经网络实战教程深入讲解
医学小达人 人气:0一、CNN简介
1. 神经网络基础
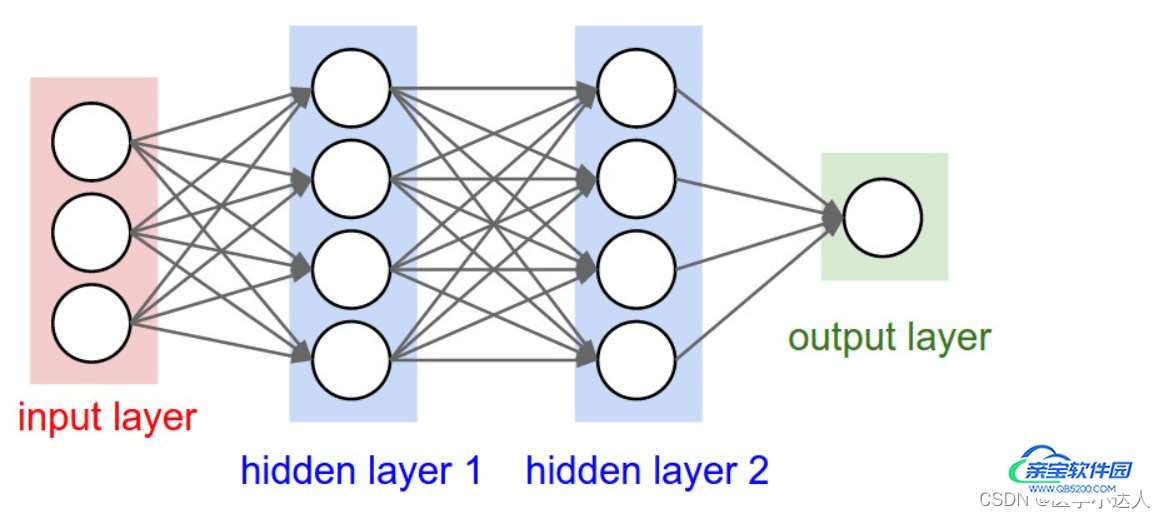
输入层(Input layer),众多神经元(Neuron)接受大量非线形输入讯息。输入的讯息称为输入向量。
输出层(Output layer),讯息在神经元链接中传输、分析、权衡,形成输出结果。输出的讯息称为输出向量。
隐藏层(Hidden layer),简称“隐层”,是输入层和输出层之间众多神经元和链接组成的各个层面。如果有多个隐藏层,则意味着多个激活函数。
2. 卷积一下哦
卷积神经网络(Convolutional Neural Network,CNN)针对全连接网络的局限做出了修正,加入了卷积层(Convolution层)和池化层(Pooling层)。通常情况下,卷积神经网络由若干个卷积层(Convolutional Layer)、激活层(Activation Layer)、池化层(Pooling Layer)及全连接层(Fully Connected Layer)组成。
下面看怎么卷积的

1.如图,可以看到:
(1)两个神经元,即depth=2,意味着有两个滤波器。
(2)数据窗口每次移动两个步长取3*3的局部数据,即stride=2。
(3)边缘填充,zero-padding=1,主要为了防止遗漏边缘的像素信息。
然后分别以两个滤波器filter为轴滑动数组进行卷积计算,得到两组不同的结果。
2.如果初看上图,可能不一定能立马理解啥意思,但结合上文的内容后,理解这个动图已经不是很困难的事情:
(1)左边是输入(7*7*3中,7*7代表图像的像素/长宽,3代表R、G、B 三个颜色通道)
(2)中间部分是两个不同的滤波器Filter w0、Filter w1
(3)最右边则是两个不同的输出
(4)随着左边数据窗口的平移滑动,滤波器Filter w0 / Filter w1对不同的局部数据进行卷积计算。
局部感知:左边数据在变化,每次滤波器都是针对某一局部的数据窗口进行卷积,这就是所谓的CNN中的局部感知机制。打个比方,滤波器就像一双眼睛,人类视角有限,一眼望去,只能看到这世界的局部。如果一眼就看到全世界,你会累死,而且一下子接受全世界所有信息,你大脑接收不过来。当然,即便是看局部,针对局部里的信息人类双眼也是有偏重、偏好的。比如看美女,对脸、胸、腿是重点关注,所以这3个输入的权重相对较大。
参数共享:数据窗口滑动,导致输入在变化,但中间滤波器Filter w0的权重(即每个神经元连接数据窗口的权重)是固定不变的,这个权重不变即所谓的CNN中的参数(权重)共享机制。
3. 卷积计算
图中最左边的三个输入矩阵就是我们的相当于输入d=3时有三个通道图,每个通道图都有一个属于自己通道的卷积核,我们可以看到输出(output)的只有两个特征图意味着我们设置的输出的d=2,有几个输出通道就有几层卷积核(比如图中就有FilterW0和FilterW1),这意味着我们的卷积核数量就是输入d的个数乘以输出d的个数(图中就是2*3=6个),其中每一层通道图的计算与上文中提到的一层计算相同,再把每一个通道输出的输出再加起来就是绿色的输出数字啦!
举例:
绿色输出的第一个特征图的第一个值:
1通道x[ : :0] 1*1+1*0 = 1 (0像素点省略)
2通道x[ : :1] 1*0+1*(-1)+2*0 = -1
3通道x[ : :2] 2*0 = 0
b = 1
输出:1+(-1)+ 0 + 1(这个是b)= 1
绿色输出的第二个特征图的第一个值:
1通道x[ : :0] 1*0+1*0 = 0 (0像素点省略)
2通道x[ : :1] 1*0+1*(-1)+2*0 = -1
3通道x[ : :2] 2*0 = 0
b = 0
输出:0+(-1)+ 0 + 1(这个是b)= 0
二、CNN实例代码
import torch import torch.nn as nn from torch.autograd import Variable import torch.utils.data as Data import torchvision import matplotlib.pyplot as plt
模型训练超参数设置,构建训练数据:如果你没有源数据,那么DOWNLOAD_MNIST=True
#Hyper prameters
EPOCH = 2
BATCH_SIZE = 50
LR = 0.001
DOWNLOAD_MNIST = True
train_data = torchvision.datasets.MNIST(
root ='./mnist',
train = True,
download = DOWNLOAD_MNIST
)数据下载后是不可以直接看的,查看第一张图片数据:
print(train_data.data.size()) print(train_data.targets.size()) print(train_data.data[0])
结果:60000张图片数据,维度都是28*28,单通道

画一个图片显示出来
# 画一个图片显示出来
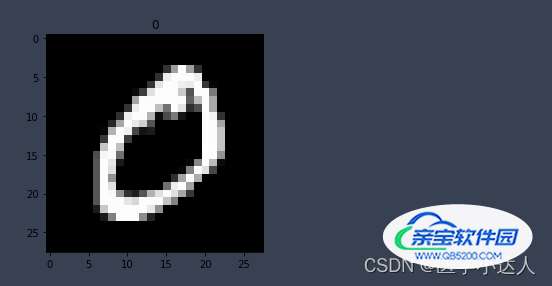
plt.imshow(train_data.data[0].numpy(),cmap='gray')
plt.title('%i'%train_data.targets[0])
plt.show()结果:
训练和测试数据准备,数据导入:
#训练和测试数据准备
train_loader=Data.DataLoader(dataset=train_data, batch_size=BATCH_SIZE, shuffle=True)
test_data=torchvision.datasets.MNIST(
root='./mnist',
train=False,
)
#这里只取前3千个数据吧,差不多已经够用了,然后将其归一化。
with torch.no_grad():
test_x=Variable(torch.unsqueeze(test_data.data, dim=1)).type(torch.FloatTensor)[:3000]/255
test_y=test_data.targets[:3000]注意:这里的归一化在此模型中区别不大
构建CNN模型:
'''开始建立CNN网络'''
class CNN(nn.Module):
def __init__(self):
super(CNN,self).__init__()
'''
一般来说,卷积网络包括以下内容:
1.卷积层
2.神经网络
3.池化层
'''
self.conv1=nn.Sequential(
nn.Conv2d( #--> (1,28,28)
in_channels=1, #传入的图片是几层的,灰色为1层,RGB为三层
out_channels=16, #输出的图片是几层
kernel_size=5, #代表扫描的区域点为5*5
stride=1, #就是每隔多少步跳一下
padding=2, #边框补全,其计算公式=(kernel_size-1)/2=(5-1)/2=2
), # 2d代表二维卷积 --> (16,28,28)
nn.ReLU(), #非线性激活层
nn.MaxPool2d(kernel_size=2), #设定这里的扫描区域为2*2,且取出该2*2中的最大值 --> (16,14,14)
)
self.conv2=nn.Sequential(
nn.Conv2d( # --> (16,14,14)
in_channels=16, #这里的输入是上层的输出为16层
out_channels=32, #在这里我们需要将其输出为32层
kernel_size=5, #代表扫描的区域点为5*5
stride=1, #就是每隔多少步跳一下
padding=2, #边框补全,其计算公式=(kernel_size-1)/2=(5-1)/2=
), # --> (32,14,14)
nn.ReLU(),
nn.MaxPool2d(kernel_size=2), #设定这里的扫描区域为2*2,且取出该2*2中的最大值 --> (32,7,7),这里是三维数据
)
self.out=nn.Linear(32*7*7,10) #注意一下这里的数据是二维的数据
def forward(self,x):
x=self.conv1(x)
x=self.conv2(x) #(batch,32,7,7)
#然后接下来进行一下扩展展平的操作,将三维数据转为二维的数据
x=x.view(x.size(0),-1) #(batch ,32 * 7 * 7)
output=self.out(x)
return output把模型实例化打印一下:
cnn=CNN() print(cnn)
结果:

开始训练:
# 添加优化方法
optimizer=torch.optim.Adam(cnn.parameters(),lr=LR)
# 指定损失函数使用交叉信息熵
loss_fn=nn.CrossEntropyLoss()
'''
开始训练我们的模型哦
'''
step=0
for epoch in range(EPOCH):
#加载训练数据
for step,data in enumerate(train_loader):
x,y=data
#分别得到训练数据的x和y的取值
b_x=Variable(x)
b_y=Variable(y)
output=cnn(b_x) #调用模型预测
loss=loss_fn(output,b_y)#计算损失值
optimizer.zero_grad() #每一次循环之前,将梯度清零
loss.backward() #反向传播
optimizer.step() #梯度下降
#每执行50次,输出一下当前epoch、loss、accuracy
if (step%50==0):
#计算一下模型预测正确率
test_output=cnn(test_x)
y_pred=torch.max(test_output,1)[1].data.squeeze()
accuracy=sum(y_pred==test_y).item()/test_y.size(0)
print('now epoch : ', epoch, ' | loss : %.4f ' % loss.item(), ' | accuracy : ' , accuracy)
'''
打印十个测试集的结果
'''
test_output=cnn(test_x[:10])
y_pred=torch.max(test_output,1)[1].data.squeeze() #选取最大可能的数值所在的位置
print(y_pred.tolist(),'predecton Result')
print(test_y[:10].tolist(),'Real Result')结果:

卷积层维度变化:
(1)输入1*28*28,即1通道,28*28维;
(2)卷积层-01:16*28*28,即16个卷积核,卷积核维度5*5,步长1,边缘填充2,维度计算公式B = (A + 2*P - K) / S + 1,即(28+2*2-5)/1 +1 = 28
(3)池化层:池化层为2*2,所以输出为16*14*14
(4)卷积层-02:32*14*14,即32卷积核,其它同卷积层-01
(5)池化层:池化层为2*2,所以输出为32*7*7;
(6)fc层:由于输出为1*10,即10个类别的概率,那么首先对最后的池化层进行压缩为二维(1,32*7*7),然后全连接层维度(32*7*7,10),最后(1,32*7*7)*(32*7*7,10)
加载全部内容