Go数组与切片轻松掌握

// 1. 创建一维数组
// 元素都是默认值
var arr1 [3]int
// 指定长度并设置初始值
var arr2 = [3]int{1, 2, 3}
var arr3 [3]int = [3]int{1, 2, 3}
// 自动推导数组长度
var arr4 = [...]int{1, 2, 3}
// 指定特定下标的元素的值，其他的为默认值
var arr5 = [3]int{1: 9}
// 2. 创建多维数组 与一维数组类似，不再赘述
var arr6 = [3][2]int{{1, 2}, {3, 4}, {5, 6}}
fmt.Println(arr1)
fmt.Println(arr2)
fmt.Println(arr3)
fmt.Println(arr4)
fmt.Println(arr5)
fmt.Println(arr6)

var arr = [3]int{1, 2, 3}
fmt.Println(arr)
arr[2] = 9
fmt.Println(arr)

var arr = [3]int{1, 2, 3}
for i := 0; i < len(arr); i++ {
	fmt.Println(arr[i])
}

var arr = [3]int{1, 2, 3}
for index, value := range arr {
	fmt.Printf("index:%d value:%d\n", index, value)
}

var arr = [3]int{1, 2, 3}
var arr2 = [3]int{1, 2, 3}
fmt.Println(arr == arr2)
var arr3 = [...]int{1, 2, 3}
fmt.Println(arr == arr3)
var arr4 = [...]int{1, 2, 4}
fmt.Println(arr == arr4)

var arr = [3]int{1, 2, 3}
var arr5 = [...]int{1, 2}
fmt.Println(arr == arr5)

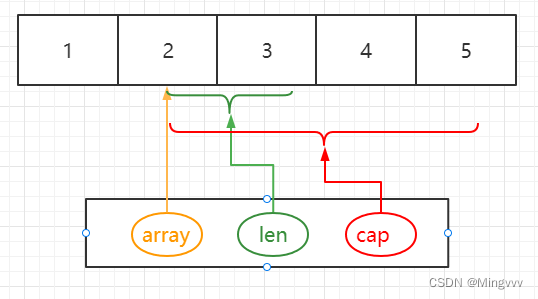
type slice struct {
    array unsafe.Pointer //指向数组的指针
    len int //切片的长度，可以理解为切片表示的元素的个数
    cap int //容量，指针所指向的数组长度（从指针位置向后）
}

//直接声明并赋值
s0 := []int{1, 2, 3, 4, 5}
//通过数组或者切片获取
arr := [...]int{1, 2, 3, 4, 5}
s1 := s0[:] // 切片 s0 中的全部元素
s2 := s0[:2] // 切片 s0 第一个元素到第二个元素
s3 := arr[3:] // 数组 arr 从第四个元素开始向后的所有元素
s4 := arr[0:0] // 创建一个空切片
//通过 make(t Type, size ...IntegerType) 初始化，
//接受的第一个 int 表示切片长度，第二个表示容量大小。如果只有一个int参数则默认长度和容量是相同的
s5 := make([]int, 5) //创建一个长度为 5 切片，
s6 := make([]int, 5, 8) //创建一个长度为 5 容量为 8 的int型切片（长度为5的部分会被初始化为默认值）
fmt.Println(s0, s1, s2, s3, s4, s5 ,s6)

//直接声明并赋值
s0 := []int{1, 2, 3, 4, 5}
fmt.Println(s0)
s0[0] = 999
fmt.Println(s0)

s0 := []int{1, 2, 3, 4, 5}
s1 := s0[1:3] //第二个元素到第三个元素
fmt.Printf("len: %d\n", len(s1))
fmt.Printf("cap: %d\n", cap(s1))
fmt.Println(s1 )

s0 := []int{1, 2, 3, 4, 5}
s1 := s0[1:3]
s2 := s1[:cap(s1)]
fmt.Printf("len: %d\n", len(s2))
fmt.Printf("cap: %d\n", cap(s2))
fmt.Println(s2)

s0 := []int{1, 2, 3, 4, 5}
s0 = append(s0, 6, 7, 8, 9, 10) //追加元素
fmt.Printf("len: %d\n", len(s0))
fmt.Printf("cap: %d\n", cap(s0))
fmt.Println(s0)
s1 := []int{11, 12, 13, 14, 15}
s0 = append(s0, s1...) //追加切片，切片需要解包
fmt.Printf("len: %d\n", len(s0))
fmt.Printf("cap: %d\n", cap(s0))
fmt.Println(s0)

s0 := make([]int, 1000)
fmt.Printf("len: %d, cap: %d\n", len(s0), cap(s0))
s0 = append(s0, make([]int, 200)...)
fmt.Printf("len: %d, cap: %d\n", len(s0), cap(s0))
s0 = append(s0, make([]int, 400)...)
fmt.Printf("len: %d, cap: %d\n", len(s0), cap(s0))

func growslice(et *_type, old slice, cap int) slice {
	...
newcap := old.cap
	doublecap := newcap + newcap
	if cap > doublecap {
		newcap = cap
	} else {
		const threshold = 256
		if old.cap < threshold {
			newcap = doublecap //小容量直接扩容到两倍容量
		} else {
			// Check 0 < newcap to detect overflow
			// and prevent an infinite loop.
			for 0 < newcap && newcap < cap {
				// Transition from growing 2x for small slices
				// to growing 1.25x for large slices. This formula
				// gives a smooth-ish transition between the two.
				//大容量取消了 1.25 倍扩容，选择了一个更为平滑的扩容方案
				newcap += (newcap + 3*threshold) / 4
			}
			// Set newcap to the requested cap when
			// the newcap calculation overflowed.
			if newcap <= 0 {
				newcap = cap
			}
		}
	}
	var overflow bool
	var lenmem, newlenmem, capmem uintptr
	// Specialize for common values of et.size.
	// For 1 we don't need any division/multiplication.
	// For goarch.PtrSize, compiler will optimize division/multiplication into a shift by a constant.
	// For powers of 2, use a variable shift.
	switch {
	case et.size == 1:
		lenmem = uintptr(old.len)
		newlenmem = uintptr(cap)
		capmem = roundupsize(uintptr(newcap))
		overflow = uintptr(newcap) > maxAlloc
		newcap = int(capmem)
	case et.size == goarch.PtrSize:
		lenmem = uintptr(old.len) * goarch.PtrSize
		newlenmem = uintptr(cap) * goarch.PtrSize
		capmem = roundupsize(uintptr(newcap) * goarch.PtrSize)
		overflow = uintptr(newcap) > maxAlloc/goarch.PtrSize
		newcap = int(capmem / goarch.PtrSize)
	case isPowerOfTwo(et.size):
		var shift uintptr
		if goarch.PtrSize == 8 {
			// Mask shift for better code generation.
			shift = uintptr(sys.Ctz64(uint64(et.size))) & 63
		} else {
			shift = uintptr(sys.Ctz32(uint32(et.size))) & 31
		}
		lenmem = uintptr(old.len) << shift
		newlenmem = uintptr(cap) << shift
		capmem = roundupsize(uintptr(newcap) << shift)
		overflow = uintptr(newcap) > (maxAlloc >> shift)
		newcap = int(capmem >> shift)
	default:
		lenmem = uintptr(old.len) * et.size
		newlenmem = uintptr(cap) * et.size
		capmem, overflow = math.MulUintptr(et.size, uintptr(newcap))
		capmem = roundupsize(capmem)
		newcap = int(capmem / et.size)
	}
	...
    return slice{p, old.len, newcap}
}