Python线性回归

时间:2022-10-20 Henry_zs 人气:0

1. 导入包

我们这次的任务是随机生成一些离散的点，然后用直线（y = w *x + b ）去拟合

首先看一下我们需要导入的包有

torch 包为我们生成张量，可以使用反向传播

matplotlib.pyplot 包帮助我们绘制曲线，实现可视化

2. 生成数据

这里我们通过rand随机生成数据，因为生成的数据在0~1之间，这里我们扩大10倍。

我们设置的batch_size，也就是数据的个数为20个，所以这里会产生维度是(20,1)个训练样本

我们假设大概的回归是 y = 2 * x + 3 的，为了保证损失不一直为0 ，这里我们添加一点噪音

最后返回x作为输入，y作为真实值label

rand [0，1]均匀分布

如果想要每次产生的随机数是一样的，可以在代码的前面设置一下随机数种子

3. 训练数据

首先，我们要建立的模型是线性的y = w * x + b ，所以我们需要先初始化w ，b

使用randn 标准正态分布随机初始化权重w，将偏置b初始化为0

为什么将权重w随机初始化？

首先，为了抑制过拟合，提高模型的泛化能力，我们可以采用权重衰减来抑制权重w的大小。因为权重过大，对应的输入x的特征就越重要，但是如果对应x是噪音的话，那么系统就会陷入过拟合中。所以我们希望得到的模型曲线是一条光滑的，对输入不敏感的曲线，所以w越小越好
那这样为什么不直接把权重初始化为0，或者说很小很小的数字呢。因为，w太小的话，那么在反向传播的时候，由于我们习惯学习率lr 设置很小，那在更新w的时候基本就不更新了。而不把权重设置为0，是因为无论训练多久，在更新权重的时候，所有权重都会被更新成相同的值，这样多层隐藏层就没有意义了。严格来说，是为了瓦解权重的对称结构

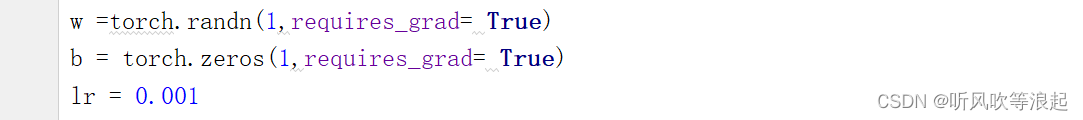
接下来可以训练我们的模型了

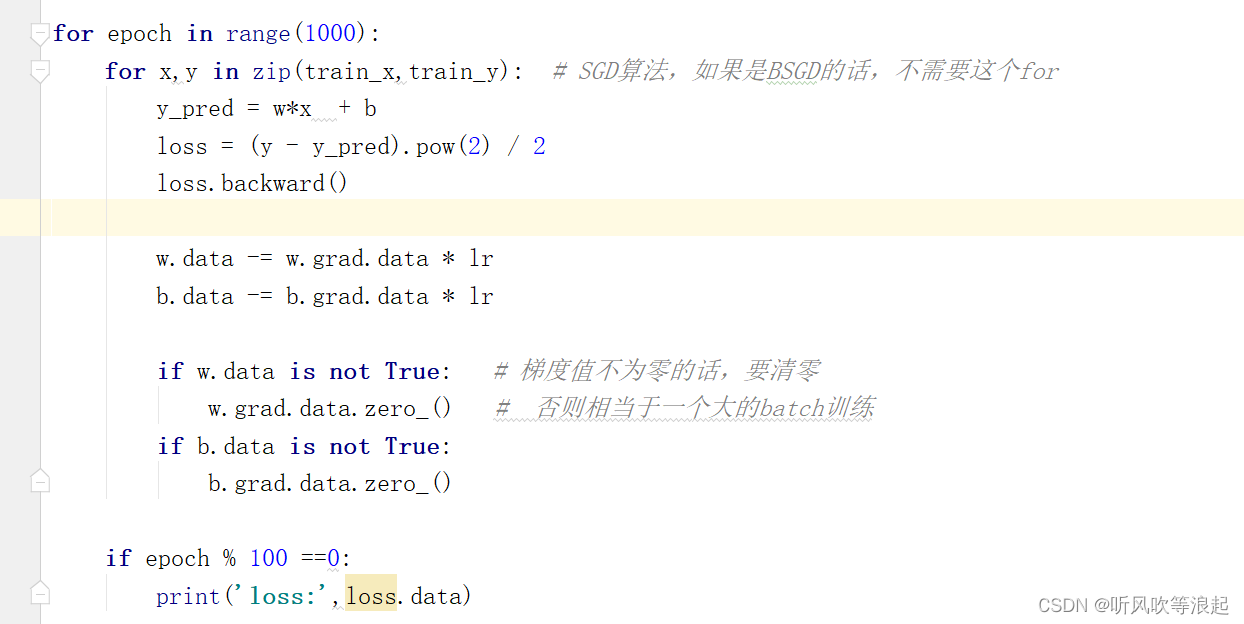
1. 将输入的特征x和对应真实值label y通过zip函数打包。将输入x经过模型 w *x + b 的预测输出预测值y

2. 计算损失函数loss，因为之前将w、b都是设置成会计算梯度的，那么loss.backward() 会自动计算w和b的梯度。用w的值data，减去梯度的值grad.data 乘上学习率lr完成一次更新

3. 当w、b梯度不为零的话，要清零。这里有两种解释，第一种是每次计算完梯度后，值会和之前计算的梯度值进行累加，而我们只是需要当前这步的梯度值，所有我们需要将之前的值清零。第二种是，因为梯度的累加，那么相当于实现一个很大的batch训练。假如一个epoch里面，梯度不进行清零的话，相当于把所有的样本求和后在进行梯度下降，而不是我们原先使用的针对单个样本进行下降的SGD算法

4. 每100次迭代后，我们打印一下损失

4. 绘制图像

scatter 相当于离散点的绘图

要绘制连续的图像，只需要给个定义域然后通过表达式 w * x +b 计算y就可以了，最后输出一下w和b，看看是不是和我们设置的w = 2，b =3 接近

5. 代码

import torch
import matplotlib.pyplot as plt
def trainSet(batch_size = 20):   # 定义训练集
    x = torch.rand(batch_size,1) * 10
    y = x * 2 + 3 + torch.randn(batch_size,1)   # y = x * 2  + 3（近似）
    return x,y
train_x, train_y = trainSet()   # 训练集
w =torch.randn(1,requires_grad= True)
b = torch.zeros(1,requires_grad= True)
lr = 0.001
for epoch in range(1000):
    for x,y in zip(train_x,train_y):  # SGD算法，如果是BSGD的话，不需要这个for
        y_pred = w*x  + b
        loss = (y - y_pred).pow(2) / 2
        loss.backward()
        w.data -= w.grad.data * lr
        b.data -= b.grad.data * lr
        if w.data is not True:   # 梯度值不为零的话，要清零
            w.grad.data.zero_()   #  否则相当于一个大的batch训练
        if b.data is not True:
            b.grad.data.zero_()
    if epoch % 100 ==0:
        print('loss:',loss.data)
plt.scatter(train_x,train_y)
x = torch.arange(0,11).view(-1,1)
y = x * w.data + b.data
plt.plot(x,y)
plt.show()
print(w.data,b.data)

输出的图像

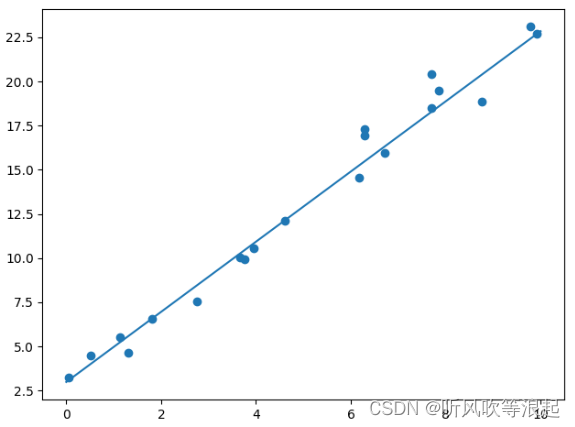
输出的结果为

这里可以看的最后的w = 1.9865和b = 2.9857 和我们设置的2，3是接近的

加载全部内容