亲宝软件园·资讯

展开

C++ AVL树

小小酥诶 人气:0

AVL树是一个高度平衡的二叉搜索树

此处AVL树结点的定义

template<class K, class V>
struct AVLTreeNode
{
	AVLTreeNode<K, V> _left;
	AVLTreeNode<K, V> _right;
	AVLTreeNode<K, V> _parent;
	pair<K, V> _kv;
	int _bf; //平衡因子
	AVLTreeNode(const pair<K, V>& kv)
		:_left(nullptr)
		,_right(nullptr)
		,_parent(nullptr)
		,_kv(kv)
		,_bf(0)
	{}
};

使用平衡因子，是维持AVL树的方法之一。

此处平衡因子 = 右子树高度 - 左子树高度。

AVL树的定义及默认构造函数

template<class K, class V>
class AVLTree
{
	typedef AVLTreeNode<K, V> Node;
public:
	AVLTree()
		:_root(nullptr)
	{}
private:
	Node* _root;
};

按照普通二叉搜索树的办法先尝试插入： bool insert(const pair<K, V>& kv);。

bool insert(const pair<K, V>& kv)
{
	if (_root == nullptr)
	{
		//插入之前是一棵空树，则插入结点变成根结点
		_root = new Node(kv);
		return true;
	}
	//找到一个NULL位置插入
	Node* parent = nullptr;
	Node* cur = _root;
	while (cur)
	{
		if (cur->_kv.first > kv.first)
		{
			parent = cur;
			cur = cur->_left;
		}
		else if (cur->_kv.first < kv.first)
		{
			parent = cur;
			cur = cur->_right;
		}
		else
		{
			//说明已经有了，就不再插入
			return false;
		}
	}
	//已找到，准备插入
	cur = new Node(kv);
	if (parent->_kv.first > kv.first)
	{
		//如果比parent小，链接到parent的左
		parent->_left = cur;
		cur->_parent = parent;
	}
	else
	{
		parent->_right = cur;
		cur->_parent = parent;
	}
}

虽然插入之后，依旧会保持二叉搜索树的特性，但是AVL树的特性可能就被破坏了。当平衡因子的绝对值是2的时候就需要进行调整。以下是AVL树特性被破坏的四种情况及解决办法：

情况一：右单旋。

结点插入后，导致左子树高度比右子树高2，其左孩子的左子树比右子树高1。

口诀：自己左高2，左孩子左高1，左单旋。

情况二：左单旋。

结点插入后，导致右子树的高度比左子树高2，其右孩子的右子树比左子树高1.

口诀：自己右高2，右孩子右高1，右单旋。

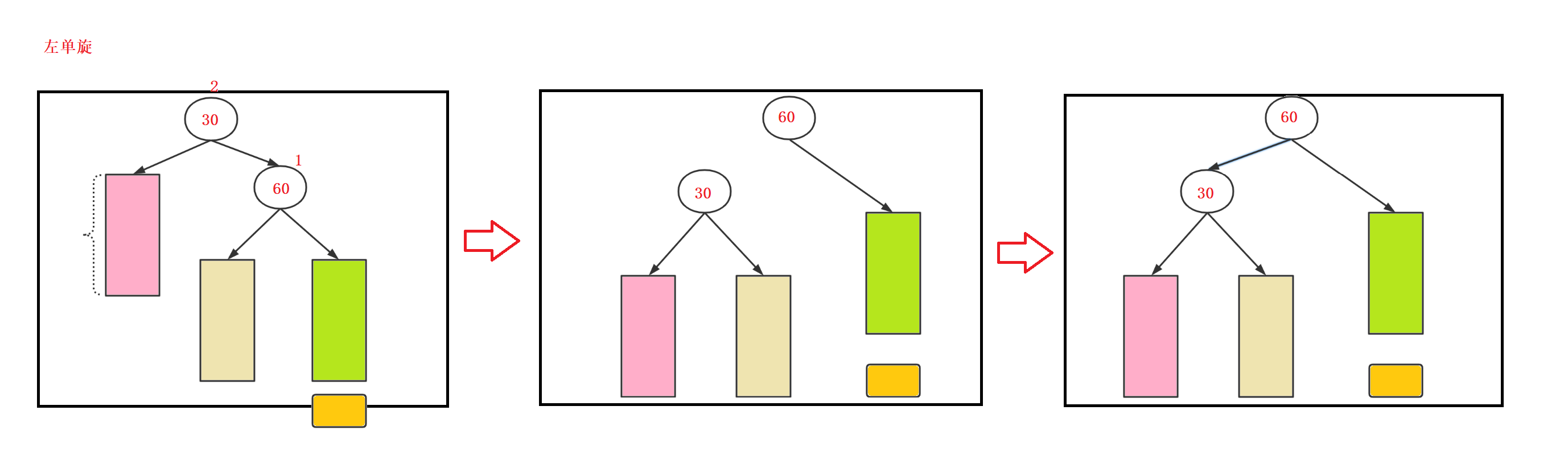
情况三：先左单旋、再右边单旋。

结点插入后，导致左子树的高度比右子树的高度高2，其左孩子的右子树比左子树高度高1.

口诀：自己左高2，左孩子右高1，先右旋后左旋。

情况四：先右单旋，再左单旋。

结点插入后右子树比左子树高2，其右孩子的左子树比右子树高1。

口诀：自己右高2，右孩子左高1，先右旋后左旋。

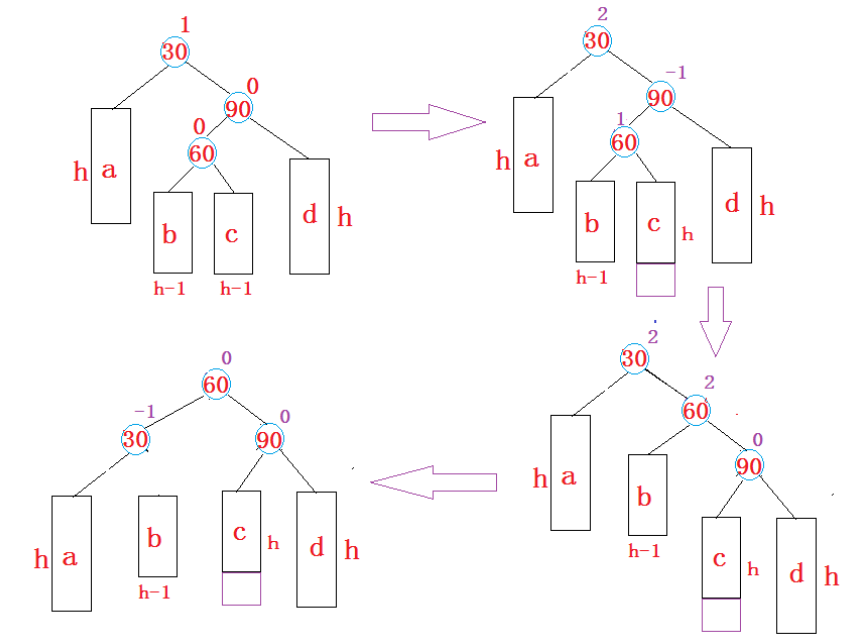
情况三和情况四种，每一种情况又衍生出了两种子问题，关乎平衡因子的更新数值。（假设此时平衡因子是-2的结点为parent， parent的左孩子为subL， subL的右孩子为subLR）

情况三的子问题

a、增加结点放在subLR的左子树。

b、增加结点放在subLR的右子树

调整后

调整后

可以看出，平衡因子的数值和结点放置位置是强相关的。虽然是同一种大情况，但是放在左子树和放在右子树，上面结点的平衡因子数值不一样。情况四也有两种子情况，和情况三的两种子情况一样。

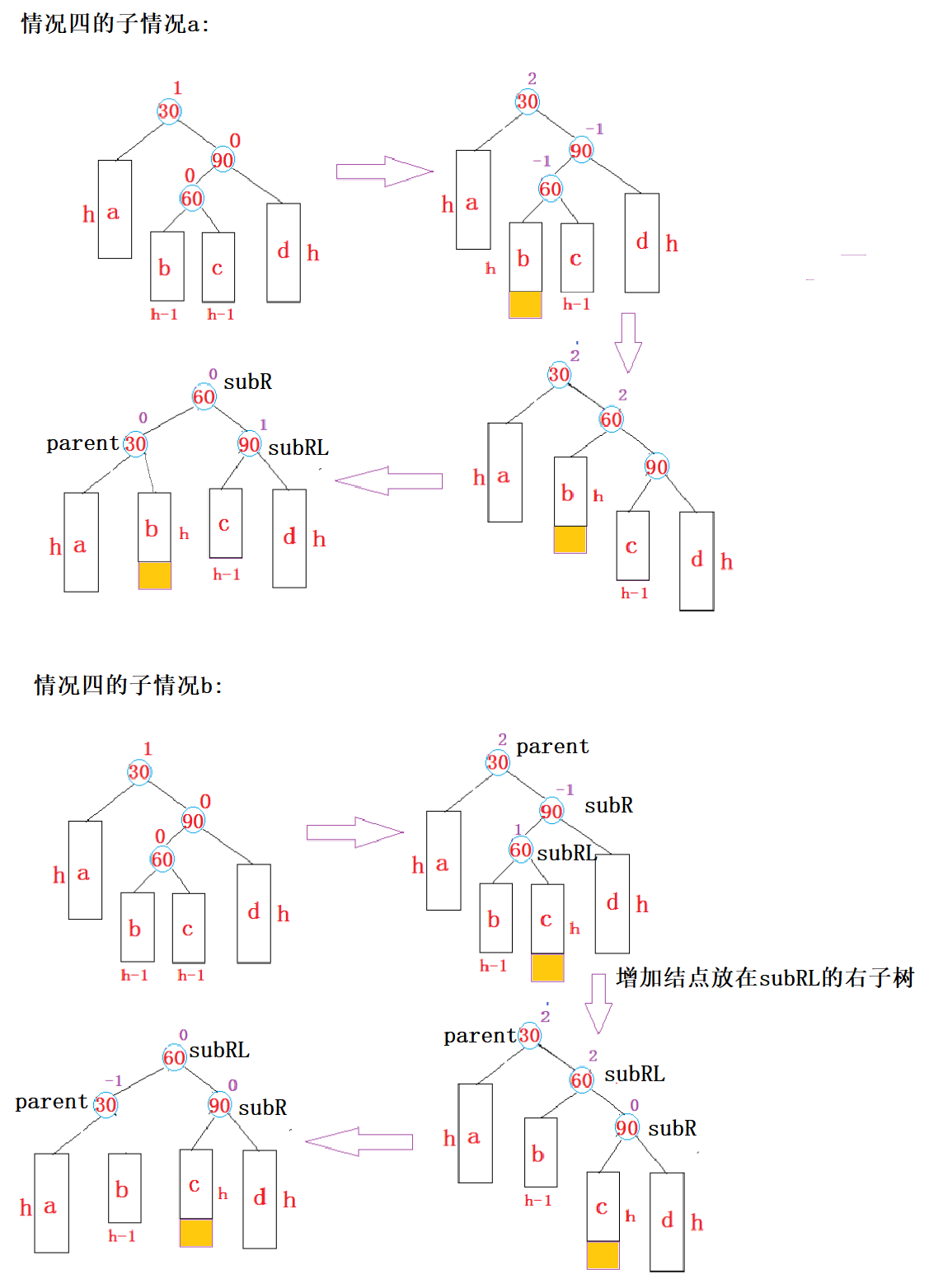
假设此时平衡因子是2的结点为parent， parent的右孩子为subR， subR的左孩子为subRL

情况四的子问题

a、增加结点放在subRL的左子树。

b、增加结点放在sub的右子树。

AVL树简单模拟插入的对应代码

namespace Blog
{
	template<class K, class V>
	struct AVLTreeNode
	{
		AVLTreeNode<K, V> _left;
		AVLTreeNode<K, V> _right;
		AVLTreeNode<K, V> _parent;
		pair<K, V> _kv;
		int _bf; //平衡因子
		AVLTreeNode(const pair<K, V>& kv)
			:_left(nullptr)
			, _right(nullptr)
			, _parent(nullptr)
			, _kv(kv)
			, _bf(0)
		{}
	};
	template<class K, class V>
	class AVLTree
	{
		typedef AVLTreeNode<K, V> Node;
	public:
		AVLTree()
			:_root(nullptr)
		{}
		bool insert(const pair<K, V>& kv)
		{
			if (_root == nullptr)
			{
				//插入之前是一棵空树，则插入结点变成根结点
				_root = new Node(kv);
				return true;
			}
			//找到一个NULL位置插入
			Node* parent = nullptr;
			Node* cur = _root;
			while (cur)
			{
				if (cur->_kv.first > kv.first)
				{
					parent = cur;
					cur = cur->_left;
				}
				else if(cur->_kv.first < kv.first)
				{
					parent = cur;
					cur = cur->_right;
				}
				else
				{
					//说明已经有了，就不再插入
					return false;
				}
			}
			//已找到，准备插入
			cur = new Node(kv);
			if (parent->_kv.first > kv.first)
			{
				//如果比parent小，链接到parent的左
				parent->_left = cur;
				cur->_parent = parent;
			}
			else
			{
				parent->_right = cur;
				cur->_parent = parent;
			}
			//更新平衡因子，平衡因子不符合时，调节树
			while (parent)
			{
				//第一步：更新平衡因子
				if (parent->_left == cur)
					parent->_bf--;
				else
					parent->_bf++;
				//检查平衡因子，如果平衡因子不符合，需要调整树
				if (0 == parent->_bf)
				{
					break;
				}
				else if (parent->_bf == 1 || parent->_bf == -1)
				{
					//继续往上更新平衡因子
					cur = parent;
					parent = cur->_parent;
				}
				else if(parent->_bf == 2 || parent->_bf == -2)
				{
					//平衡因子不符合，说明左子树和右子树高度之差为2，需要调整树
					//情况一：右单旋
					if (parent->_bf == -2 && cur->_bf == -1)
					{
						RotateR(parent);
					}
					else if (parent->_bf == 2 && cur->_bf == 1) // 左单旋
					{
						RotateL(parent);
					}
					else if (parent->_bf == -2 && cur->_bf == 1)
					{
						RotateLR(parent);
					}
					else if (parent->_bf == 2 && cur->_bf == -1)
					{
						RotateRL(parent);
					}
					else
					{
						assert(false);
					}
				}
				else
				{
					//说明插入之前，这颗树就已经不符合AVL树的特性了
					assert(false);
				}
			}
			return true;
		}
	private:
		void RotateR(Node* parent)
		{
			Node* subL = parent->_left;
			Node* subLR = subLR->_right;
			parent->_left = subLR;
			if (subLR)
			{
				subLR->_parent = parent;
			}
			Node* parentParent = parent->_parent;
			subL->_right = parent;
			parent->_parent = subL;
			if (parent == _root)
			{
				subL->_parent = nullptr;
				_root = subL;
			}
			else
			{
				if (parentParent->_left = parent)
				{
					parentParent->_left = subL;
					subL->_parent = parentParent;
				}
				else
				{
					parentParent->_right = subL;
					subL->_parent = parentParent;
				}
			}
			//调节后，重新更新平衡因子
			parent->_bf = subL->_bf = 0;
		}
		void RotateL(Node* parent)
		{
			Node* subR = parent->_right;
			Node* subRL = subRL->_left;
			parent->_right = subRL;
			if (subRL)
				suRL->_parent = parent;
			Node* parentParent = parent->_parent;
			subR->_left = parent;
			parent->_parent = subR;
			if (parent == _root)
			{
				subR->_parent = nullptr;
				_root = subR;
			}
			else
			{
				if (parentParent->_left = parent)
				{
					parentParent->_left = subR;
					subR->_parent = parentParent;
				}
				else
				{
					parentParent->_right = subR;
					subR->_parent = parentParent;
				}
			}
			subR->_bf = parent->_bf = 0;
		}
		void RotateLR(Node* parent)
		{
			Node* subL = parent->_left;
			Node* subLR = subL->_right;
			int bf = subLR->_bf; //用于后面判断加在subRL的左子树还是右子树
			RotateL(parent->_left);
			RotateR(parent);
			//它的两种子情况，更新的平衡因子不一样
			if (bf == -1)
			{
				//加在subLR的左子树
				parent->_bf = 1;
				subL->_bf = 0;
				subLR->_bf = 0;
			}
			else if (bf == 1)
			{
				//加在右子树
				parent->_bf = 0;
				subL->_bf = -1;
				subLR->_bf = 0;
			}
			else if (bf == 0)
			{
				parent->_bf = 0;
				subL->_bf = 0;
				subLR->_bf = 0;
			}
			else
			{
				assert(false);
			}
		}
		void RotateRL(Node* parent)
		{
			Node* subR = parent->_right;
			Node* subRL = subL->_left;
			int bf = subRL->_bf; //用于后面判断加在subRL的左子树还是右子树
			RotateL(parent->_right);
			RotateR(parent);
			//它的两种子情况，更新的平衡因子不一样
			if (bf == -1)
			{
				//加在subRL的子树
				parent->_bf = 0;
				subR->_bf = 0;
				subRL->_bf = 1;
			}
			else if (bf == 1)
			{
				//加在左子树
				parent->_bf = -1;
				subR->_bf = 0;
				subRL->_bf = 0;
			}
			else if (bf == 0)
			{
				parent->_bf = 0;
				subR->_bf = 0;
				subRL->_bf = 0;
			}
			else
			{
				assert(false);
			}
		}
	private:
		Node* _root;
	};
}

加载全部内容
相关教程
猜你喜欢
用户评论