C++坐标转换
略游 人气:0一、前言
严格来说,瓦片的角度并不是45度。因为为了美术作图方便,图片的宽高比一般为2:1,如下图所示,它的实际角度为arctan(1/2),不过这个数值对我们不重要。正如鱼香肉丝没有鱼一般,叫它45度瓦片也无妨,由于它是一个菱形,所以这里我们称它为菱形瓦片。
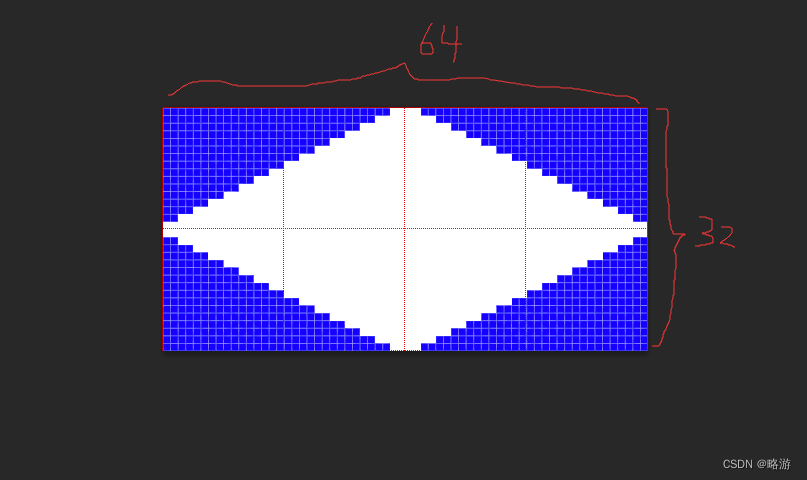
宽高比为2:1的菱形瓦片
或许有人认为任意角度的瓦片都是可以的,其实不然,因为我们要考虑线条锯齿的画法,如果采用非整数比,则线条不是规律的(非像素游戏或许可以试试)。所以最常见的比例为2:1,其次是1:1。
还有一个问题,我们观察菱形的四分之一部分,它将一个矩形一分为二。我们当然期望它是平分的,然而这根本做不到,因为它不是理论的对角线。对于正方形瓦片来说,边缘是不会重叠的。而菱形瓦片不可避免的边缘存在重叠。

边缘必然重叠
二、定义
我们定义地图上的一个点为世界(World)坐标,它是连续的,用浮点数表示。然后格子的索引叫地图(Map)坐标,它是离散的,用有符号整数表示。不过这里地图坐标的取值未考虑负数,如要使用负数的地图坐标则需要对代码略微修改。
比如下图的p点,我们假设格子宽10像素。则其世界坐标为(54,67),而地图坐标为(5,6)。

矩形瓦片示例
三、矩形瓦片
矩形瓦片的代码很简单,如下:
//! 矩形瓦片地图
template<Vector2 TILE_SIZE>
class Rectangle
{
public:
/**
* @brief 地图坐标 -> 世界坐标
*/
constexpr Vector2 Map2World(const Point& xy)
{
return toVector2(xy) * TILE_SIZE;
}
/**
* @brief 世界坐标 -> 地图坐标
*/
constexpr Point World2Map(const Vector2& pos)
{
return toPoint(pos / TILE_SIZE);
}
};四、菱形瓦片
1.斜菱形瓦片
这里的斜指的是,整个地图拼出来是斜着的,也是一个菱形,如下图所示(这是常用的算法):
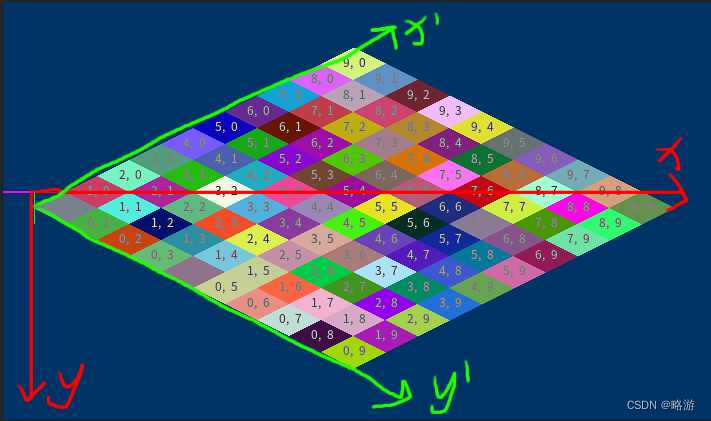
斜菱形瓦片
我们令x'y'为地图(格子)坐标,xy为世界(像素)坐标,其中wh为瓦片宽高,则有如下关系:
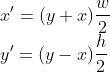
上面这个式子通过简单的变换,就可以得出:
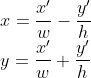
转换代码如下,这里就体现出了将瓦片大小(TILE_SIZE)作为模板的好处了,其中除2的操作会自动合并为常量表达式,世界坐标到地图坐标的转换其中加了0.5,是为了四舍五入。
//! 斜45度瓦片地图
template<Vector2 TILE_SIZE>
class DiamondSlant
{
public:
/**
* @brief 地图坐标 -> 世界坐标
*/
constexpr Vector2 Map2World(const Point& xy)
{
return { (xy[1] + xy[0]) * TILE_SIZE[0] / 2.0, (xy[1] - xy[0]) * TILE_SIZE[1] / 2.0};
}
/**
* @brief 世界坐标 -> 地图坐标
*/
constexpr Point World2Map(const Vector2& pos)
{
Vector2 xy_div = pos / TILE_SIZE;
return toPoint(Vector2{ xy_div[0] - xy_div[1] + 0.5, xy_div[0] + xy_div[1] - 0.5 });
}
};2.正菱形瓦片
下面这种整体也是一个矩形,它的特点是x轴移动瓦片宽度,y轴只移动半个瓦片高度,当y为奇数时,x再往右移动半个瓦片宽度。(有些文章是y为偶数时x移动,原理相同)

正菱形瓦片
容易得到,从格子坐标到世界坐标,如下:
当y为偶数时:
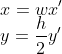
当y为奇数时:

这里出现和上面不一样的事了,无法简单的逆推公式来表示x'y'。因为通过世界(像素)坐标无法轻松得到它的地图(格子)坐标的y是奇数还是偶数。
从格子坐标到世界坐标的代码如下:
/**
* @brief 地图坐标 -> 世界坐标
*/
constexpr Vector2 Map2World(const Point& xy)
{
Vector2 pos = { TILE_SIZE[0] * xy[0] , TILE_SIZE[1] / 2 * xy[1] };
if (xy[1] % 2 != 0)
{//奇数行向右偏移 w / 2
pos[0] += TILE_SIZE[0] / 2;
}
return pos;
}而从世界坐标到格子坐标则比较麻烦了,如下,我们划分网格:

划分网格
明显格子大小为(w,h),记世界坐标pos所在的格子为p,则有:
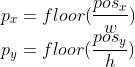
来看单个划分网格内,如下:

单个划分格子
设瓦片格子坐标为xy,则当 pos在菱形内时,有:
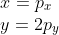
当 pos在菱形外时,四个角则分别判断:右下角偏移(0,1);左下角偏移(-1,1);左上角偏移(-1,-1);右上角偏移(0,-1)。
所以最终实现代码如下:
//! 平菱形瓦片地图
template<Vector2 TILE_SIZE>
class DiamondFlat
{
public:
/**
* @brief 地图坐标 -> 世界坐标
*/
constexpr Vector2 Map2World(const Point& xy)
{
Vector2 pos = { TILE_SIZE[0] * xy[0] , TILE_SIZE[1] / 2 * xy[1] };
if (xy[1] % 2 != 0)
{//奇数行向右偏移 w / 2
pos[0] += TILE_SIZE[0] / 2;
}
return pos;
}
/**
* @brief 世界坐标 -> 地图坐标
*/
constexpr Point World2Map(const Vector2& pos)
{
constexpr Vector2 TILE_SIZE_HALF = TILE_SIZE / 2.0;
//四分之一矩形面积
constexpr real s = Each::AccumulateMul(TILE_SIZE_HALF);
//先计算矩形下标
Point p = toPoint(pos / TILE_SIZE);
//在矩形内坐标
Vector2 p1 = pos - toVector2(p) * TILE_SIZE - TILE_SIZE_HALF;
//点围成矩形面积
real sp = abs(p1[0] * TILE_SIZE_HALF[1]) + abs(p1[1] * TILE_SIZE_HALF[0]);
p[1] *= 2;
if (s < sp)
{
if (p1[0] > 0 && p1[1] > 0)
return p + Point{ 0, 1 };
else if (p1[0] < 0 && p1[1] > 0)
return p + Point{ -1, 1 };
else if (p1[0] < 0 && p1[1] < 0)
return p + Point{ -1, -1 };
else if (p1[0] > 0 && p1[1] < 0)
return p + Point{ 0, -1 };
else
return p;
}
else
{
return p;
}
}
};五、点在菱形内判断
如下图所示,以菱形中心为原点建立坐标系:
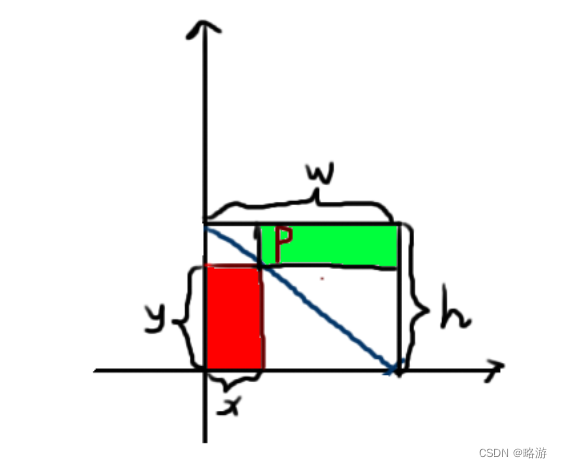
p在对角线上时
当p点在菱形上时,红绿区域面积相等(对角线平分面积),所以:

(红色区域加了两次,将其中变成一个绿色区域)
则当p点在菱形外时,
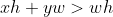
;在菱形内时

源码位置:传送门
加载全部内容