JS 树结构

时间:2022-09-28 一碗周人气:0

什么是树

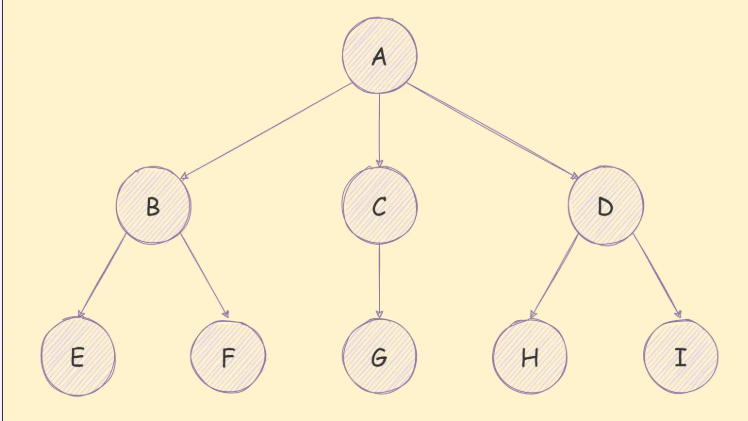
在现实生活中，相信每个人对树都很熟悉，不管是柳树、杨树还是桃树，可以说树在我们生活中随处可见；在计算机世界，树是一种分层结构的抽象模型，

如下图所示：

树结构的应用有很多，就比如公司的组织架构，就可以用树来表示，如下图：

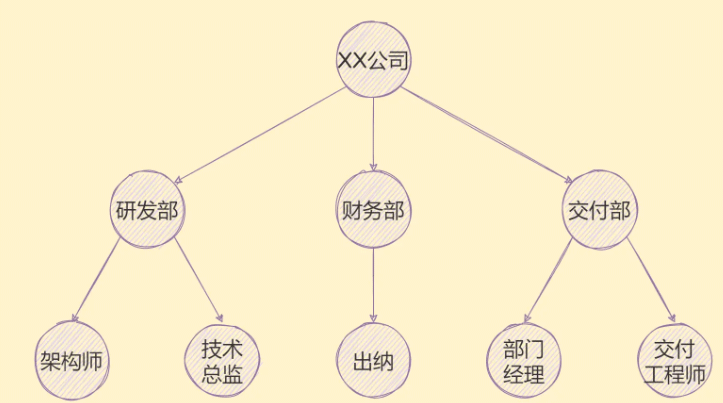
除了组织架构，像族谱、省市等都可以使用树结构来表示。

树的术语

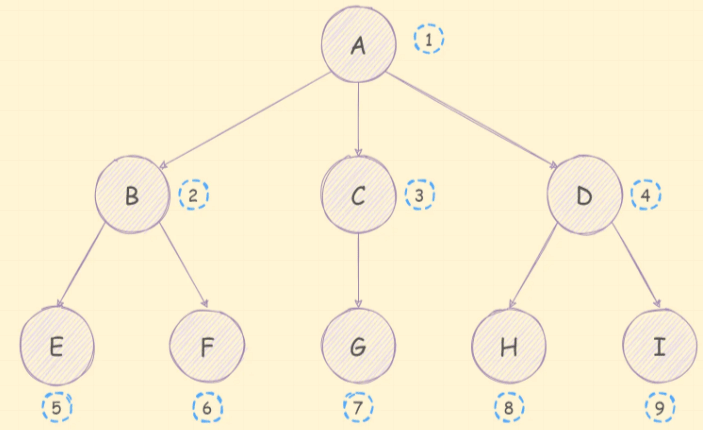
树有很多的术语，如下图：

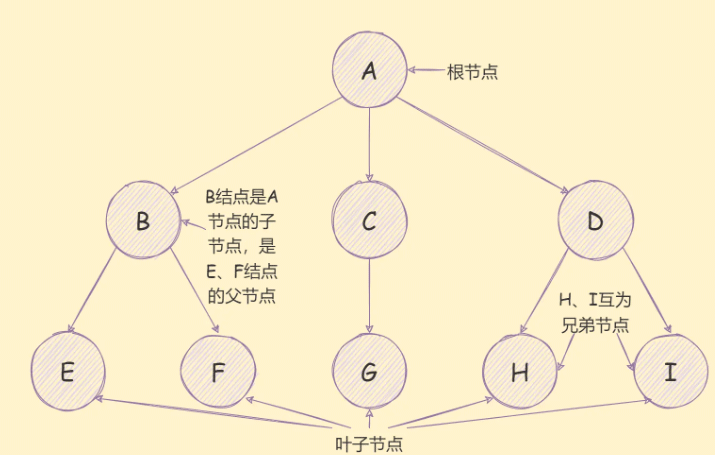
树：n(n≥0)个节点所构成的有限集合，当n=0时，称为空树；
节点的度：节点的子树个数，例如B节点的度就是2，A节点的度就是3；
树的度：树的所有节点中最大的度数，例如上图中，树的度是3；
叶子节点：度为0的节点，也叫叶节点；
子节点：如上图；
兄弟节点：如上图；
根节点：如上图；
树的深度：树中所有结点中的最大层次，例如上图中树的深度就是3；
节点的层次：例如E节点的层次就是3，节点的层次就是父节点层次+1，根节点的层次为1；
路径：一个节点到另一个节点的通道，例如A→H的路径就是A D H；
路径长度：一个节点到另一个节点的距离，例如A→H的路径就是3。

JavaScript中的树

树结构可以说是前端中最常见的数据结构之一，比如说DOM树、级联选择、树形组件等等；

JavaScript中并没有提供树这个数据结构，但是我们可以通过对象和数组来模拟一个树，

例如下面这段代码：

const tree = {
  value: 'A',
  children: [
    {
      value: 'B',
      children: [
        { value: 'E', children: null },
        { value: 'F', children: null },
      ],
    },
    {
      value: 'C',
      children: [{ value: 'G', children: null }],
    },
    {
      value: 'D',
      children: [
        { value: 'H', children: null },
        { value: 'I', children: null },
      ],
    },
  ],
}

广度优先和深度优点遍历算法

深度优先

所谓的深度优先遍历算法，就是尽可能深的去搜索树的分支，它的遍历顺序如下图：

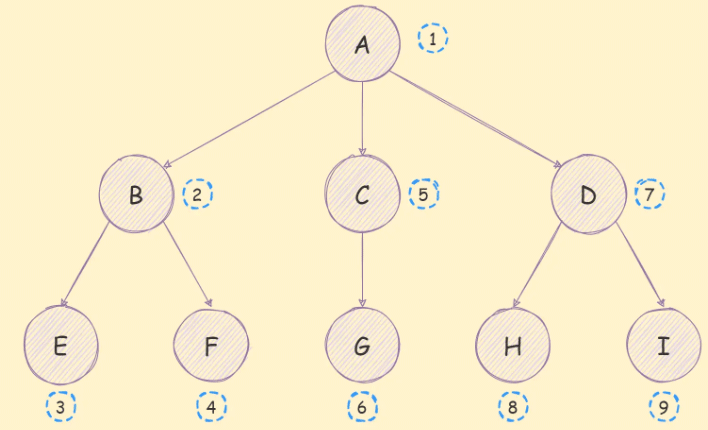
实现思路如下：

访问根节点；
对根节点的children持续进行深度优先遍历（递归）；

实现代码如下：

function dfs(root) {
  console.log(root.value)
  root.children && root.children.forEach(dfs) // 与下面一致
  // if (root.children) {
  //   root.children.forEach(child => {
  //     dfs(child)
  //   })
  // }
}
dfs(tree) // 这个tree就是前面定义的那个树
/* 结果
A
B
E
F
C
G
D
H
I
*/

可以看到，和图中的顺序是一致的，也就是说我们的算法没有问题。

广度优先

所谓的广度优先就是依次访问离根节点近的节点，它的遍历顺序如下图：

实现思路如下：

创建要给队列，把根节点入队；
把队头出队并访问；
把队头的children依次入队；
重复执行2、3步，直到队列为空。

实现代码如下：

function bfs(root) {
  // 1. 新建队列 跟节点入队
  const q = [root]
  // 4 重复执行
  while (q.length > 0) {
    const node = q.shift() // 2 队头出队
    console.log(node.value)
    // 3 队头 children 依次入队
    node.children &&
      node.children.forEach(child => {
        q.push(child)
      })
  }
}
bfs(tree)
/* 结果
A
B
C
D
E
F
G
H
I
*/

可以看到，和图中的顺序是一致的，也就是说我们的算法没有问题。

加载全部内容