pytorch 计算图

前言：

今天聊一聊 pytorch 的计算图和自动求导，我们先从一个简单例子来看，下面是一个简单函数建立了 yy 和 xx 之间的关系

然后我们结点和边形式表示上面公式：

上面的式子可以用图的形式表达，接下来我们用 torch 来计算 x 导数，首先我们创建一个 tensor 并且将其requires_grad设置为True表示随后反向传播会对其进行求导。

x = torch.tensor(3.,requires_grad=True)

然后写出

y = 3*x**2 + 4*x + 2

y.backward()
x.grad

通过调用y.backward()来进行求导，这时就可以通过x.grad来获得x的导数

x.requires_grad_(False)

可以通过requires_grad_让x不参与到自动求导

for epoch in range(3):
  y = 3*x**2 + 4*x + 2
  y.backward()
  print(x.grad)
  x.grad.zero_()

如果这里没有调用x.grad_zero_()就是把每次求导数和上一次求导结果进行累加。

链式法则

相对于 z 对 x 求偏导时，我们可以将 y 看成常数，这样 x 导数是 1 那么

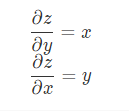
x = torch.tensor([1.,2.,3.],requires_grad=True)

y = x * 2 + 3
z = y **2

out = z.mean()
out.backward()

print(out) #tensor(51.6667, grad_fn=<MeanBackward0>)

print(x.grad) #tensor([ 6.6667, 9.3333, 12.0000])

对于一个简单的网络，我们可以手动计算梯度，但是如果摆在你面前的是一个有152 层的网络怎么办？或者该网络有多个分支。这时你的计算复杂程度可想而知。接下来会带来更深入自动求导内部机制