Android贝塞尔曲线
小北的博客 人气:0在平面内任选 3 个不共线的点,依次用线段连接。
在第一条线段上任选一个点 D。计算该点到线段起点的距离 AD,与该线段总长 AB 的比例。
根据上一步得到的比例,从第二条线段上找出对应的点 E,使得 AD:AB = BE:BC。
连接这两点 DE。
从新的线段 DE 上再次找出相同比例的点 F,使得 DF:DE = AD:AB = BE:BC。
到这里,我们就确定了贝塞尔曲线上的一个点 F。接下来,请稍微回想一下中学所学的极限知识,让选取的点 D 在第一条线段上从起点 A 移动到终点 B,找出所有的贝塞尔曲线上的点 F。所有的点找出来之后,我们也得到了这条贝塞尔曲线。
回过头来看这条贝塞尔曲线,为了确定曲线上的一个点,需要进行两轮取点的操作,因此我们称得到的贝塞尔曲线为二次曲线(这样记忆很直观,但曲线的次数其实是由前面提到的伯恩斯坦多项式决定的)。
三个点的基本关系如下:
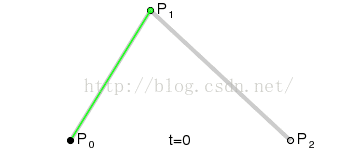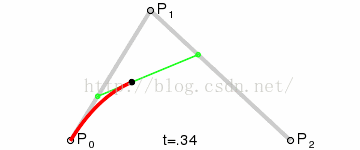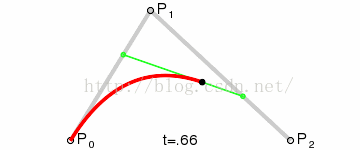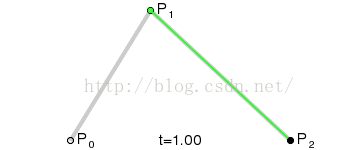
Android 的Path类提供了绘制二阶贝塞尔曲线的方法,使用方法如下:
public class CurveView extends View{
private float mSupX;
private float mSupY;
private int mWidth;
private int mHeight;
private Paint mPaint;
private Path mPath;
public CurveView(Context context) {
super(context);
}
public CurveView(Context context, AttributeSet attrs) {
super(context, attrs, 0);
mPaint = new Paint();
mPaint.setStyle(Paint.Style.STROKE);
mPaint.setStrokeWidth(10);
mPath = new Path();
}
@Override
protected void onMeasure(int widthMeasureSpec, int heightMeasureSpec) {
int widthSize = MeasureSpec.getSize(widthMeasureSpec);
int widthMode = MeasureSpec.getMode(widthMeasureSpec);
int heightSize = MeasureSpec.getSize(heightMeasureSpec);
int heightMode = MeasureSpec.getMode(heightMeasureSpec);
if (widthMode == MeasureSpec.EXACTLY) {
mWidth = widthSize;
}
if (heightMode == MeasureSpec.EXACTLY) {
mHeight = heightSize;
}
setMeasuredDimension(mWidth, mHeight);
}
@Override
protected void onDraw(Canvas canvas) {
mPath.reset();
mPath.moveTo(mWidth / 5, mHeight / 2); //设置起点
mPath.quadTo(mSupX, mSupY, mWidth * 4 / 5, mHeight / 2); //设置辅助点和终点
canvas.drawPath(mPath, mPaint);
canvas.drawPoint(mSupX, mSupY, mPaint);
super.onDraw(canvas);
}
@Override
public boolean onTouchEvent(MotionEvent event) {
switch (event.getAction()){
case MotionEvent.ACTION_MOVE:
mSupX = event.getX();
mSupY = event.getY();
invalidate();
}
return true;
}
}Draw以后效果如下:

加载全部内容